Obliczenia: rachunki, dowody i gry
Co da się obliczyć, a czego się nie da? Dziś informatycy pytają o to rutynowo w kontekście przeróżnych problemów, jednak pierwsza odpowiedź na to pytanie pojawiła się na dobrą sprawę, jeszcze zanim ktokolwiek zdążył je zadać, i wprawiła środowisko naukowe w zakłopotanie.
Na początku XX wieku matematycy wierzyli, że każdy problem matematyczny da się rozstrzygnąć za pomocą obliczeń. U szczytu tego optymizmu, w 1928 roku, David Hilbert postulował opracowanie uniwersalnej metody pozwalającej na obliczenie prawdziwości dowolnego stwierdzenia sformułowanego w języku logiki pierwszego rzędu – czyli za pomocą spójników logicznych i, lub, nie oraz kwantyfikatorów istnieje i dla każdego. Niecałe 10 lat później Alan Turing udowodnił, że taki algorytm nie istnieje. A więc są rzeczy, których obliczyć się nie da! Ale co to właściwie znaczy? Wydaje się, że wiemy, co to znaczy obliczyć. Jednak aby wykazać, że czegoś obliczyć się nie da, potrzebujemy więcej niż tylko nieformalnej intuicji. Potrzebujemy definicji obliczenia.
Rachunek jako obliczenie
Aby sformułować definicję obliczenia, Alan Turing przeanalizował pracę
rachmistrza, czyli człowieka przeprowadzającego rachunki. Rachmistrz, mówi
Turing, prowadzi obliczenia na papierze. Papier jest wprawdzie dwuwymiarowy,
ale podczas obliczeń nie czynimy z tego użytku. Przyjmiemy więc, że
obliczenie prowadzimy na papierze jednowymiarowym, czyli taśmie. Taśma
ta jest podzielona na komórki, odpowiadające kratkom na papierze.
W każdej komórce można napisać symbol. Komórka ma ograniczoną
powierzchnię, a oko ludzkie ma ograniczoną rozdzielczość, więc bez
zmniejszenia ogólności możemy przyjąć, że symbole pochodzą ze
skończonego alfabetu. Działania rachmistrza zależą od obserwowanych
symboli i jego stanu umysłu. Umysł ludzki jest obiektem skończonym i liczba
odróżnialnych stanów, które może przyjmować, jest skończona (choć
wielka i trudna do oszacowania). Rachmistrz jest w stanie jednocześnie
obserwować jedynie pewną niewielką liczbę komórek, powiedzmy
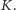

Jakie działania wykonuje rachmistrz? Spróbujmy je opisać w terminach
możliwie najprostszych, niepodzielnych akcji. Rachmistrz może napisać
symbol w obserwowanej komórce taśmy. Może też zmienić obserwowaną
komórkę na dowolną inną, jeśli tylko potrafi ją natychmiast zidentyfikować.
Jakie komórki mogą być natychmiast zidentyfikowane? Komórki, która jest
bardzo daleko od wszystkich obserwowanych komórek, nie da się łatwo
odróżnić od jej sąsiadów. Rachmistrz jest w stanie dokładnie określić
odległość jednym rzutem oka tylko wtedy, gdy odległość ta nie jest zbyt
duża, powiedzmy nie większa niż
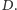 Przyjmijmy, że rachmistrz może
przesunąć każdą obserwowaną komórkę o co najwyżej
Przyjmijmy, że rachmistrz może
przesunąć każdą obserwowaną komórkę o co najwyżej
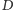 pozycji
w lewo lub w prawo. Ponadto, w czasie prowadzenia obliczeń rachmistrz
zmienia stan umysłu. Reasumując, pojedynczy krok obliczenia obejmuje
napisanie symbolu w niektórych obserwowanych komórkach, przesunięcie
niektórych obserwowanych komórek o co najwyżej
pozycji
w lewo lub w prawo. Ponadto, w czasie prowadzenia obliczeń rachmistrz
zmienia stan umysłu. Reasumując, pojedynczy krok obliczenia obejmuje
napisanie symbolu w niektórych obserwowanych komórkach, przesunięcie
niektórych obserwowanych komórek o co najwyżej
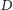 pozycji oraz
zmianę stanu umysłu.
pozycji oraz
zmianę stanu umysłu.
Nasz rachmistrz jest profesjonalistą, który bezbłędnie opanował reguły
prowadzenia rachunków, ale nie ma własnej inwencji: każdy kolejny krok jego
rachunku jest całkowicie zdeterminowany przez zawartość obserwowanych
komórek i stan umysłu. Reguły stosowane przez rachmistrza można opisać
funkcją, która ciągowi symboli
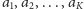 znajdujących się
w obserwowanych komórkach i stanowi umysłu
znajdujących się
w obserwowanych komórkach i stanowi umysłu
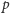 przyporządkowuje
nowy ciąg symboli
przyporządkowuje
nowy ciąg symboli
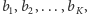 ciąg przesunięć obserwowanych
komórek
ciąg przesunięć obserwowanych
komórek
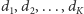 oraz nowy stan
oraz nowy stan
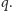 To znaczy, że
rachmistrz w pierwszej obserwowanej komórce pisze symbol
To znaczy, że
rachmistrz w pierwszej obserwowanej komórce pisze symbol
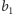 (jeśli
(jeśli
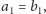 to rachmistrz nic nie pisze), a następnie zmienia obserwowaną
komórkę na komórkę znajdującą się o
to rachmistrz nic nie pisze), a następnie zmienia obserwowaną
komórkę na komórkę znajdującą się o
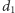 pozycji w prawo, jeśli
pozycji w prawo, jeśli
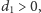 lub o
lub o
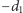 pozycji w lewo, jeśli
pozycji w lewo, jeśli
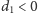 (jeśli
(jeśli
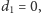 obserwowana komórka się nie zmienia). Następnie rachmistrz
postępuje podobnie dla komórek
obserwowana komórka się nie zmienia). Następnie rachmistrz
postępuje podobnie dla komórek
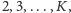 po czym zmienia stan
umysłu na
po czym zmienia stan
umysłu na
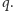 Rachmistrz zaczyna obliczenie w pewnym ustalonym stanie
umysłu, mając na taśmie zapisane dane początkowe i obserwując pierwszych
Rachmistrz zaczyna obliczenie w pewnym ustalonym stanie
umysłu, mając na taśmie zapisane dane początkowe i obserwując pierwszych
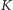 komórek taśmy. Potem wykonuje akcje wskazywane przez
reguły. Obliczenie kończy się, gdy rachmistrz osiągnie odpowiedni stan
umysłu, również z góry ustalony. Wynik obliczenia jest zapisany na
taśmie.
komórek taśmy. Potem wykonuje akcje wskazywane przez
reguły. Obliczenie kończy się, gdy rachmistrz osiągnie odpowiedni stan
umysłu, również z góry ustalony. Wynik obliczenia jest zapisany na
taśmie.
Zwróćmy uwagę, że pracę rachmistrza może wykonać każdy, jeśli tylko dostanie odpowiednie instrukcje: listę symboli alfabetu, listę możliwych stanów, stan początkowy, stan końcowy oraz powyższą funkcję. A skoro tak, to dlaczego nie mogłaby tej pracy wykonywać maszyna? W ciągu 10 lat od ogłoszenia koncepcji maszyny Turinga pierwsze programowalne komputery zostaną skonstruowane w Niemczech, Wielkiej Brytanii i Stanach Zjednoczonych...
Wróćmy jednak do problemu obliczalności. Alan Turing przyjął, że uniwersalna metoda obliczania odpowiedzi na pytanie to po prostu taki zestaw instrukcji dla rachmistrza: wymagamy jedynie tego, żeby dla każdych danych początkowych rachmistrz kończył obliczenie i zapisywał na taśmie poprawną odpowiedź. W przypadku problemu postawionego przez Hilberta dane początkowe to stwierdzenie zapisane za pomocą symboli logicznych, a odpowiedź brzmi tak lub nie, zależnie od tego, czy dane stwierdzenie jest prawdziwe, czy fałszywe. Turing udowodnił, że istnieją problemy, dla których nie ma uniwersalnej metody obliczania odpowiedzi i że zagadnienie opisane przez Hilberta jest jednym z takich problemów.
Dowód jako obliczenie
Wyniki Turinga zdają się obnażać słabość matematyki: oto są rzeczy, których nie da się obliczyć. Ale przecież matematyka to nie tylko rachunki! Czym różni się praca matematyka próbującego udowodnić twierdzenie od pracy rachmistrza? Rachmistrz działa zgodnie z instrukcjami, jednoznacznie wskazującymi każdy kolejny krok obliczeń. Matematyk, prowadząc rozumowanie, również kieruje się pewnymi regułami, jednak reguły te nie mówią, jaki krok należy wykonać, ale raczej jakie są możliwe kroki. Spośród wielu możliwych kroków za każdym razem trzeba wybrać jeden i nie ma żadnej gwarancji, że akurat ten doprowadzi nas do celu. Aby uwzględnić to zjawisko w modelu maszyny Turinga, wystarczy zmodyfikować funkcję opisującą reguły obliczenia. Funkcja opisująca pracę rachmistrza wskazywała kolejną akcję na podstawie symboli w obserwowanych komórkach i bieżącego stanu umysłu. Funkcja opisująca pracę matematyka będzie wskazywała zbiór możliwych akcji. Taki model obliczeń nazywamy niedeterministyczną maszyną Turinga. Model opisany wcześniej to maszyna deterministyczna.

Dla uproszczenia rozważań przyjmijmy, że interesują nas wyłącznie pytania
typu tak/nie. Nawet dla takich pytań różne ciągi wyborów maszyny
niedeterministycznej mogą prowadzić do różnych odpowiedzi. Co
zatem jest wynikiem obliczeń? Wróćmy na chwilę do zjawiska, które
usiłujemy modelować, czyli do dowodzenia twierdzeń. Twierdzenie
uznajemy za udowodnione, gdy odkryjemy ciąg kroków prowadzący do
celu. Nie przejmujemy się tym, że wiele wyborów okazuje się złych
i kolejne próby dowodu lądują w koszu
 Wypada nam zatem
przyjąć, że wynikiem obliczenia niedeterministycznej maszyny Turinga dla
ustalonych danych początkowych jest tak, jeśli choć jeden ciąg wyborów
prowadzi do odpowiedzi tak. Jeśli wszystkie ciągi wyborów prowadzą
do odpowiedzi nie, wtedy przyjmujemy, że wynikiem obliczenia jest
nie.
Wypada nam zatem
przyjąć, że wynikiem obliczenia niedeterministycznej maszyny Turinga dla
ustalonych danych początkowych jest tak, jeśli choć jeden ciąg wyborów
prowadzi do odpowiedzi tak. Jeśli wszystkie ciągi wyborów prowadzą
do odpowiedzi nie, wtedy przyjmujemy, że wynikiem obliczenia jest
nie.
Innymi słowy, maszyna konstruuje dowód na to, że odpowiedź brzmi tak: należy odpowiedzieć tak wtedy, gdy istnieje choć jeden dowód.
Wydawać by się mogło, że niedeterministyczne maszyny potrafią rozwiązać
więcej problemów niż deterministyczne. Okazuje się jednak, że tak nie jest:
każdą niedeterministyczną maszynę Turinga
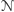 można zasymulować
za pomocą maszyny deterministycznej
można zasymulować
za pomocą maszyny deterministycznej
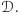 Symulacja ta nie jest trudna do
wyobrażenia: wystarczy równolegle rozważać wszystkie możliwe wybory
maszyny
Symulacja ta nie jest trudna do
wyobrażenia: wystarczy równolegle rozważać wszystkie możliwe wybory
maszyny
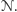 Obliczenia obu maszyn rozpoczynają się tak samo: na
taśmie zapisane są dane początkowe, maszyny znajdują się w stanie
początkowym, obserwują pierwsze
Obliczenia obu maszyn rozpoczynają się tak samo: na
taśmie zapisane są dane początkowe, maszyny znajdują się w stanie
początkowym, obserwują pierwsze
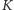 komórek taśmy. Maszyna
komórek taśmy. Maszyna
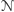 w tym momencie wybiera jedną z kilku możliwych akcji.
Maszyna
w tym momencie wybiera jedną z kilku możliwych akcji.
Maszyna
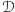 natomiast kopiuje zawartość taśmy tyle razy, ile
możliwych akcji ma maszyna
natomiast kopiuje zawartość taśmy tyle razy, ile
możliwych akcji ma maszyna
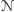 (kolejne kopie oddziela dodatkowym
symbolem, nieużywanym przez
(kolejne kopie oddziela dodatkowym
symbolem, nieużywanym przez
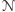 ). Ponadto, w każdej kopii zaznacza
pozycję komórek obserwowanych przez
). Ponadto, w każdej kopii zaznacza
pozycję komórek obserwowanych przez
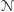 oraz stan maszyny
oraz stan maszyny
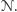 Następnie, w każdej z tych kopii
Następnie, w każdej z tych kopii
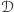 symuluje inny wybór
symuluje inny wybór
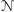 : modyfikuje zawartość taśmy, przesuwa obserwowane komórki
i zmienia stan maszyny zgodnie z opisem akcji znajdującym się w zbiorze reguł
maszyny
: modyfikuje zawartość taśmy, przesuwa obserwowane komórki
i zmienia stan maszyny zgodnie z opisem akcji znajdującym się w zbiorze reguł
maszyny
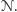 W ten sposób
W ten sposób
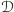 ma na taśmie wszystkie możliwe
rezultaty obliczenia
ma na taśmie wszystkie możliwe
rezultaty obliczenia
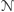 po jednym kroku. Dalej symulacja przebiega
podobnie: dla każdego rezultatu obliczenia wykonujemy tyle kopii, ile
maszyna
po jednym kroku. Dalej symulacja przebiega
podobnie: dla każdego rezultatu obliczenia wykonujemy tyle kopii, ile
maszyna
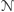 ma możliwości do wyboru, a potem w każdej
kopii wykonujemy inną akcję. Po kolejnych rundach symulacji mamy na
taśmie zapisane wszystkie możliwe rezultaty obliczenia
ma możliwości do wyboru, a potem w każdej
kopii wykonujemy inną akcję. Po kolejnych rundach symulacji mamy na
taśmie zapisane wszystkie możliwe rezultaty obliczenia
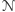 po
po
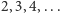 krokach. Jeśli w dowolnym momencie otrzymamy wynik tak,
to kończymy symulację i udzielamy odpowiedzi tak. Jeśli natomiast dojdziemy
do sytuacji, w której wszystkie rezultaty odpowiadają zakończonemu
obliczeniu
krokach. Jeśli w dowolnym momencie otrzymamy wynik tak,
to kończymy symulację i udzielamy odpowiedzi tak. Jeśli natomiast dojdziemy
do sytuacji, w której wszystkie rezultaty odpowiadają zakończonemu
obliczeniu
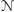 z wynikiem nie, to kończymy obliczenie z odpowiedzią
nie.
z wynikiem nie, to kończymy obliczenie z odpowiedzią
nie.
Gra jako obliczenie
Wiemy już, że dodanie niedeterministycznych wyborów do naszego modelu obliczeń nie pozwala na rozwiązywanie nowych problemów. Spróbujmy więc czegoś więcej. Wyobraźmy sobie, że matematyk próbuje przekonać swoją sceptyczną koleżankę, że potrafi udowodnić pewne twierdzenie. Przypuśćmy, że matematyk mówi: „Aby udowodnić twierdzenie, dowodzę lemat A, potem lemat B, a z nich otrzymuję twierdzenie jako wniosek C”. Koleżanka mogłaby odpowiedzieć: „Dobrze, ale jak dowodzisz lemat B?”. Matematyk na to: „Robię najpierw obserwację B.1, potem korzystam z ogólnego faktu B.2 i dostaję lemat jako wniosek B.3”. Koleżanka: „W porządku, pokaż, jak dostajesz wniosek B.3”. Matematyk podaje dowód wniosku. Po takiej wymianie zdań sceptyczna koleżanka przyjmuje, że matematyk faktycznie zna dowód twierdzenia, choć nie zobaczyła go w całości. Koleżanka wierzy bowiem, że matematyk nie tylko potrafił odpowiedzieć na pytania, które usłyszał, ale że ma kompletną strategię odpowiedzi na wszystkie możliwe pytania.
Taki sposób weryfikacji istnienia dowodu modelujemy za pomocą alternujących maszyn Turinga. Stany maszyny alternującej są podzielone na dwa zbiory: stany egzystencjalne, kontrolowane przez matematyka, oraz stany uniwersalne, kontrolowane przez jego sceptyczną koleżankę. Poza tym maszyna alternująca wygląda tak jak niedeterministyczna, tzn. obliczenie wymaga dokonywania wyborów spośród dostępnych kroków. Jeśli bieżący stan jest egzystencjalny, to matematyk wybiera kolejny krok obliczenia. Jeśli jednak stan jest uniwersalny, to kolejny krok wybiera sceptyczna koleżanka, a matematyk musi umieć poradzić sobie niezależnie od wyboru koleżanki. Maszyna udziela odpowiedzi tak, jeśli matematyk ma strategię prowadzącą do wyniku tak, niezależnie od wyborów koleżanki.
Czy w tak poszerzonym modelu da się rozwiązać więcej problemów? Okazuje
się, że odpowiedź znowu jest negatywna. Dość łatwo jest symulować
maszynę alternującą
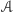 za pomocą maszyny niedeterministycznej
za pomocą maszyny niedeterministycznej
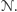 Symulacja jest podobna do poprzedniej: na taśmie trzymamy częściowe
rezultaty obliczeń
Symulacja jest podobna do poprzedniej: na taśmie trzymamy częściowe
rezultaty obliczeń
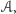 ale tym razem tylko niektóre. Mianowicie,
jeśli w rozważanym częściowym rezultacie maszyna
ale tym razem tylko niektóre. Mianowicie,
jeśli w rozważanym częściowym rezultacie maszyna
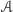 jest
w stanie egzystencjalnym, to maszyna
jest
w stanie egzystencjalnym, to maszyna
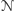 niedeterministycznie
wybiera jeden z możliwych ruchów maszyny
niedeterministycznie
wybiera jeden z możliwych ruchów maszyny
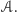 Jeśli natomiast
Jeśli natomiast
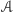 jest w stanie uniwersalnym, to
jest w stanie uniwersalnym, to
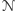 wykonuje wszystkie
możliwe ruchy w oddzielnych kopiach częściowego rezultatu, podobnie jak
wcześniej. Maszyna
wykonuje wszystkie
możliwe ruchy w oddzielnych kopiach częściowego rezultatu, podobnie jak
wcześniej. Maszyna
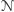 akceptuje, jeśli wszystkie częściowe rezultaty
odpowiadają ukończonemu obliczeniu maszyny
akceptuje, jeśli wszystkie częściowe rezultaty
odpowiadają ukończonemu obliczeniu maszyny
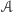 z wynikiem
tak.
z wynikiem
tak.
Pożytki z niedeterminizmu i alternacji
Pokazaliśmy, że zarówno maszyny niedeterministyczne, jak i alternujące
rozwiązują dokładnie te same problemy co maszyny deterministyczne. Czy to
znaczy, że z niedeterminizmu i alternacji nie ma żadnego pożytku?
Dotychczas interesowaliśmy się wyłącznie tym, czy odpowiedź na pytanie da
się obliczyć, czy też nie. Jednak dużo istotniejsze jest pytanie, czy odpowiedź
da się obliczyć szybko. Rozważmy następujący problem: spośród 400
uczniów należy wybrać 100, którzy będą spali w jednej dużej sali podczas
wycieczki szkolnej, należy jednak przestrzegać reguły, aby pewne pary
uczniów nie znalazły się jednocześnie w tej sali; lista takich zakazanych par jest
również częścią danych początkowych. Jak można taki problem
rozwiązać? Można rozważyć po kolei wszystkie możliwe podzbiory 100
uczniów i dla każdego zbioru sprawdzić, czy zawiera zakazaną parę,
czy nie. Ale czy ta metoda jest praktyczna? Wymaga ona rozważenia
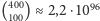 podzbiorów. Ta liczba na papierze wygląda niegroźnie,
ale wedle szacunków kosmologów wielokrotnie przekracza liczbę atomów
w obserwowalnym wszechświecie. Trudno więc sobie wyobrazić, że tą
metodą można uzyskać wynik nawet przy użyciu bardzo szybkiego
komputera...
podzbiorów. Ta liczba na papierze wygląda niegroźnie,
ale wedle szacunków kosmologów wielokrotnie przekracza liczbę atomów
w obserwowalnym wszechświecie. Trudno więc sobie wyobrazić, że tą
metodą można uzyskać wynik nawet przy użyciu bardzo szybkiego
komputera...
Z drugiej strony, niedeterministyczna maszyna Turinga mogłaby po prostu
przejrzeć listę uczniów i niedeterministycznie zaznaczyć 100 spośród nich,
a następnie sprawdzić, czy wybrany podzbiór nie zawiera żadnej
zakazanej pary. Ta metoda wymaga przejrzenia listy uczniów raz dla każdej
zakazanej pary, a więc nie więcej niż
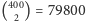 razy. Większości
współczesnych komputerów nie zajęłoby to nawet sekundy. Kłopot polega na
tym, że komputery są realizacją deterministycznej maszyny Turinga,
a więc nie mogą po prostu niedeterministycznie wygenerować podzbioru
uczniów.
razy. Większości
współczesnych komputerów nie zajęłoby to nawet sekundy. Kłopot polega na
tym, że komputery są realizacją deterministycznej maszyny Turinga,
a więc nie mogą po prostu niedeterministycznie wygenerować podzbioru
uczniów.
Pytanie brzmi więc: jak szybko można symulować maszyny niedeterministyczne
(lub alternujące) za pomocą maszyn deterministycznych. Obie opisane
przez nas symulacje są wykładnicze: jeśli maszyna niedeterministyczna
o
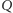 stanach wykonuje
stanach wykonuje
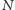 kroków, to symulująca maszyna
deterministyczna wykonuje mniej więcej
kroków, to symulująca maszyna
deterministyczna wykonuje mniej więcej
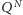 kroków. Na przykład dla
niedeterministycznej maszyny rozwiązującej problem wyboru 100 uczniów taka
symulacja zajęłaby więcej czasu niż bezpośrednie przejrzenie wszystkich
możliwych podzbiorów. Czy da się to zrobić lepiej? Konkretnie, czy da się
zasymulować obliczenie niedeterministyczne długości
kroków. Na przykład dla
niedeterministycznej maszyny rozwiązującej problem wyboru 100 uczniów taka
symulacja zajęłaby więcej czasu niż bezpośrednie przejrzenie wszystkich
możliwych podzbiorów. Czy da się to zrobić lepiej? Konkretnie, czy da się
zasymulować obliczenie niedeterministyczne długości
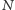 za
pomocą deterministycznego obliczenia długości
za
pomocą deterministycznego obliczenia długości
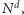 dla pewnej
stałej
dla pewnej
stałej
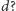 Na to pytanie do dziś nikomu nie udało się udzielić
odpowiedzi. Odpowiedź twierdząca oznaczałaby, że problemy rozwiązywalne
w wielomianowo wielu krokach na maszynie niedeterministycznej da się
rozwiązać w wielomianowo wielu krokach na maszynie deterministycznej, czyli
że
Na to pytanie do dziś nikomu nie udało się udzielić
odpowiedzi. Odpowiedź twierdząca oznaczałaby, że problemy rozwiązywalne
w wielomianowo wielu krokach na maszynie niedeterministycznej da się
rozwiązać w wielomianowo wielu krokach na maszynie deterministycznej, czyli
że
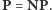 Odpowiedź przecząca nie dawałaby bezpośrednich
wniosków dotyczących problemu
Odpowiedź przecząca nie dawałaby bezpośrednich
wniosków dotyczących problemu
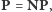 ale byłaby nie mniej
sensacyjna. Problemy rozwiązywalne na maszynie alternującej w wielomianowo
wielu krokach tworzą tzw. klasę
ale byłaby nie mniej
sensacyjna. Problemy rozwiązywalne na maszynie alternującej w wielomianowo
wielu krokach tworzą tzw. klasę
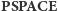 (nazwa pochodzi od
równoważnej charakteryzacji przez maszyny deterministyczne używające
wielomianowej liczby komórek taśmy). O tej klasie również nie wiadomo,
czy jest równa klasie
(nazwa pochodzi od
równoważnej charakteryzacji przez maszyny deterministyczne używające
wielomianowej liczby komórek taśmy). O tej klasie również nie wiadomo,
czy jest równa klasie
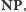 czy też jest od niej większa. Choć pytanie to
jest mniej słynne, rozstrzygnięcie tego problemu byłoby również wielkim
przełomem.
czy też jest od niej większa. Choć pytanie to
jest mniej słynne, rozstrzygnięcie tego problemu byłoby również wielkim
przełomem.
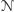 prowadzący do wyniku tak,
to w końcu się na niego natkniemy. Ale co, jeśli taki ciąg wyborów nie istnieje?
Wtedy wiemy, że każdy ciąg wyborów maszyny
prowadzący do wyniku tak,
to w końcu się na niego natkniemy. Ale co, jeśli taki ciąg wyborów nie istnieje?
Wtedy wiemy, że każdy ciąg wyborów maszyny
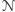 prowadzi do
odpowiedzi nie w skończenie wielu krokach. Czy z tego wynika, że nasza
symulacja też się skończy po skończenie wielu krokach? Okazuje się, że tak.
Gwarancji udziela nam następujący lemat Königa: jeśli każdy wierzchołek w
drzewie ma skończenie wiele dzieci i każda gałąź jest skończona, to całe
drzewo też jest skończone.
prowadzi do
odpowiedzi nie w skończenie wielu krokach. Czy z tego wynika, że nasza
symulacja też się skończy po skończenie wielu krokach? Okazuje się, że tak.
Gwarancji udziela nam następujący lemat Königa: jeśli każdy wierzchołek w
drzewie ma skończenie wiele dzieci i każda gałąź jest skończona, to całe
drzewo też jest skończone.