Informatyk gra na giełdzie
Nasz znajomy informatyk zdecydował się zainwestować część swoich oszczędności na giełdzie papierów wartościowych. Jak na informatyka przystało, do grania na giełdzie postanowił zaprząc komputer. W tym celu, korzystając z najnowszych trendów sztucznej inteligencji, napisał program, który na podstawie przeszłych notowań giełdowych przewiduje, jak kurs akcji będzie się zmieniał w przyszłości, i podejmuje decyzje o kupnie bądź sprzedaży. Nasz znajomy przetestował program, uruchamiając go na dużym zbiorze archiwalnych notowań. Zastanawia się teraz, jak dobrze jego program sobie poradził – stanął zatem przed problemem wyznaczenia najlepszej możliwej gry na giełdzie, jeśli znamy wszystkie notowania.

Model gry na giełdzie będzie następujący. Mamy daną tablicę
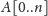 z notowaniami giełdowymi w kolejnych dniach:
z notowaniami giełdowymi w kolejnych dniach:
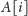 oznacza cenę jednej akcji w
oznacza cenę jednej akcji w
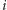 -tym dniu (dla uproszczenia
przyjmiemy, że mamy tylko jeden rodzaj akcji). Na początku dysponujemy
kwotą
-tym dniu (dla uproszczenia
przyjmiemy, że mamy tylko jeden rodzaj akcji). Na początku dysponujemy
kwotą
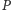 i możemy wykonać nie więcej niż
i możemy wykonać nie więcej niż
 operacji
kupna-sprzedaży akcji (zakładamy, że możemy kupować ułamkową liczbę
akcji). Zauważmy, że nie potrzebujemy wykonywać operacji równolegle (tzn.
przed każdym kupnem opłaca się nam najpierw sprzedać wszystkie
posiadane akcje). Ponadto warto też kupować akcje za całą dostępną
kwotę. Z tego wynika, że jeśli pierwszą operację kupna przeprowadzimy
w dniu
operacji
kupna-sprzedaży akcji (zakładamy, że możemy kupować ułamkową liczbę
akcji). Zauważmy, że nie potrzebujemy wykonywać operacji równolegle (tzn.
przed każdym kupnem opłaca się nam najpierw sprzedać wszystkie
posiadane akcje). Ponadto warto też kupować akcje za całą dostępną
kwotę. Z tego wynika, że jeśli pierwszą operację kupna przeprowadzimy
w dniu
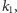 a odpowiadającą jej sprzedaż w dniu
a odpowiadającą jej sprzedaż w dniu
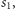 to po tej
operacji będziemy mieli kwotę
to po tej
operacji będziemy mieli kwotę
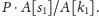 Naszym celem jest
zmaksymalizowanie kwoty po wszystkich
Naszym celem jest
zmaksymalizowanie kwoty po wszystkich
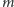 operacjach, czyli
iloczynu
operacjach, czyli
iloczynu
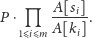 |
Możemy pozbyć się mnożeń i dzieleń, logarytmując powyższy wzór. Innymi słowy, równoważnie możemy zmaksymalizować sumę
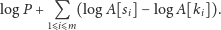 |
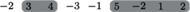
Rys. 1 Przykładowa tablica
 dla
dla
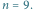 Optymalne rozwiązanie dla
Optymalne rozwiązanie dla
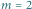 to
dwa zaznaczone fragmenty o sumach 7 i 6.
to
dwa zaznaczone fragmenty o sumach 7 i 6.

W końcu jeśli wprowadzimy pomocniczą tablicę
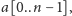 która zawierać
będzie zmiany zlogarytmowanych notowań, tzn.
która zawierać
będzie zmiany zlogarytmowanych notowań, tzn.
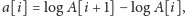 to
nasze zadanie sprowadzi się do wybrania co najwyżej
to
nasze zadanie sprowadzi się do wybrania co najwyżej
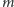 rozłącznych
fragmentów
rozłącznych
fragmentów
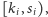 które maksymalizują sumę liczb do nich
należących (Rys. 1):
które maksymalizują sumę liczb do nich
należących (Rys. 1):
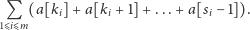 |
Dla
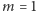 jest to klasyczne zadanie znajdowania fragmentu tablicy
o największej sumie, które może być znane Czytelnikom. Z kolei jego
uogólnienie dla
jest to klasyczne zadanie znajdowania fragmentu tablicy
o największej sumie, które może być znane Czytelnikom. Z kolei jego
uogólnienie dla
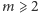 było treścią zadania pt. Tanie linie, które
pojawiło się podczas weekendowej rundy Potyczek Algorytmicznych
2012. Oba problemy mają liczne ciekawe rozwiązania. W dalszej części
artykułu przedstawimy, z pożytkiem dla znajomego informatyka, aż osiem
z nich.
było treścią zadania pt. Tanie linie, które
pojawiło się podczas weekendowej rundy Potyczek Algorytmicznych
2012. Oba problemy mają liczne ciekawe rozwiązania. W dalszej części
artykułu przedstawimy, z pożytkiem dla znajomego informatyka, aż osiem
z nich.
***
Na początek przypomnijmy, jak rozwiązać zadanie dla
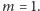 Algorytm
A1 jest bardzo prosty: w czasie
Algorytm
A1 jest bardzo prosty: w czasie
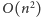 możemy przebadać wszystkie
możliwe fragmenty, ustalając lewy koniec fragmentu i iterując po kolejnych
możliwych prawych końcach.
możemy przebadać wszystkie
możliwe fragmenty, ustalając lewy koniec fragmentu i iterując po kolejnych
możliwych prawych końcach.
Algorytm A2 wykona to samo w optymalnym czasie
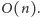 Przeglądamy
elementy tablicy od lewej do prawej i trzymamy
Przeglądamy
elementy tablicy od lewej do prawej i trzymamy
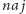 – maksymalny
fragment w przedziale
– maksymalny
fragment w przedziale
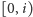 oraz
oraz
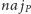 – maksymalny fragment,
który dotyka prawego końca tego przedziału (tzn. kończy się elementem
– maksymalny fragment,
który dotyka prawego końca tego przedziału (tzn. kończy się elementem
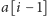 ). Na początek
). Na początek
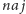 i
i
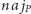 inicjujemy zerami,
a następnie wykonujemy pętlę:
inicjujemy zerami,
a następnie wykonujemy pętlę:

Zadanie dla
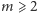 można rozwiązać, korzystając z metody programowania
dynamicznego i uogólniając algorytm A2. Przez
można rozwiązać, korzystając z metody programowania
dynamicznego i uogólniając algorytm A2. Przez
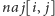 oznaczmy
największą sumę liczb z przedziału
oznaczmy
największą sumę liczb z przedziału
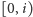 zawartych w co najwyżej
zawartych w co najwyżej
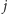 rozłącznych fragmentach, a przez
rozłącznych fragmentach, a przez
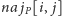 to samo, ale
z zastrzeżeniem, że ostatni fragment zawiera element
to samo, ale
z zastrzeżeniem, że ostatni fragment zawiera element
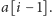 Rekurencja
(bez uwzględniania warunków brzegowych) jest następująca:
Rekurencja
(bez uwzględniania warunków brzegowych) jest następująca:

Rozwiązaniem jest
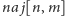 ; algorytm A3 działa w czasie
; algorytm A3 działa w czasie
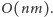


Rys. 2 Rozwiązania optymalne zawierające fragment
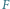 oraz fragmenty
oraz fragmenty
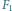 i
i
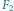 (szare obszary), jak również nowe rozwiązanie optymalne dla dwóch fragmentów
(przerywana linia).
(szare obszary), jak również nowe rozwiązanie optymalne dla dwóch fragmentów
(przerywana linia).
Poszukując szybszego algorytmu dla
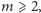 spróbujmy odpowiedzieć na
pytanie: Czy, mając optymalne rozwiązanie dla
spróbujmy odpowiedzieć na
pytanie: Czy, mając optymalne rozwiązanie dla
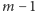 fragmentów, da się
je łatwo rozszerzyć do
fragmentów, da się
je łatwo rozszerzyć do
 fragmentów? Zatrzymajmy się nad
przypadkiem
fragmentów? Zatrzymajmy się nad
przypadkiem
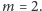 Powiedzmy, że fragment
Powiedzmy, że fragment
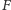 ma największą
sumę. Jak może wyglądać optymalne rozwiązanie dla dwóch fragmentów
ma największą
sumę. Jak może wyglądać optymalne rozwiązanie dla dwóch fragmentów
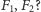 Rozważmy dwa przypadki (Rys. 2).
Rozważmy dwa przypadki (Rys. 2).
- (1) Jeden z fragmentów (powiedzmy
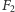 ) jest rozłączny
z
) jest rozłączny
z
 Wtedy
Wtedy
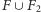 jest poprawnym rozwiązaniem,
zatem z optymalności
jest poprawnym rozwiązaniem,
zatem z optymalności
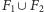 dostajemy, że
dostajemy, że
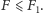 Ale z optymalności
Ale z optymalności
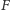 mamy
mamy
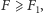 zatem fragmenty
zatem fragmenty
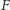 i
i
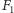 mają tę samą
sumę. To pokazuje, że
mają tę samą
sumę. To pokazuje, że
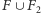 jest również optymalne.
jest również optymalne.
- (2) Oba fragmenty
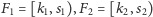 przecinają
przecinają
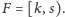 Jeśli
Jeśli
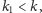 to fragment
to fragment
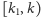 musi mieć sumę zero
(inaczej moglibyśmy poprawić
musi mieć sumę zero
(inaczej moglibyśmy poprawić
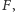 dodając do niego
ten fragment, lub poprawić
dodając do niego
ten fragment, lub poprawić
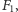 usuwając ten fragment).
Zatem usunięcie tego fragmentu z
usuwając ten fragment).
Zatem usunięcie tego fragmentu z
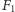 nie zmieni wyniku.
Analogicznie dla
nie zmieni wyniku.
Analogicznie dla
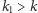 fragment
fragment
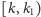 musi mieć
sumę zero i można go dodać do
musi mieć
sumę zero i można go dodać do
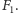 Stosując takie samo
rozumowanie do prawego końca fragmentu
Stosując takie samo
rozumowanie do prawego końca fragmentu
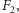 dostajemy,
że istnieje optymalne rozwiązanie
dostajemy,
że istnieje optymalne rozwiązanie
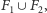 w którym
w którym
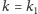 i
i
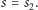
Udowodniliśmy zatem, że możemy znaleźć optymalne rozwiązanie dla
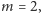 rozszerzając fragment
rozszerzając fragment
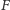 o największej sumie. W tym celu:
albo (1) dodajemy nowy fragment o największej sumie, który jest rozłączny
z
o największej sumie. W tym celu:
albo (1) dodajemy nowy fragment o największej sumie, który jest rozłączny
z
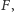 albo (2) znajdujemy fragment o najmniejszej sumie zawarty
całkowicie w
albo (2) znajdujemy fragment o najmniejszej sumie zawarty
całkowicie w
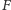 i usuwamy go, dzieląc
i usuwamy go, dzieląc
 na dwa fragmenty.
Wybieramy ten wariant, który lepiej poprawia wynik.
na dwa fragmenty.
Wybieramy ten wariant, który lepiej poprawia wynik.
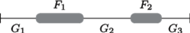
Rys. 3 Podział tablicy po wykonaniu dwóch faz algorytmu.
Zachęceni tym sukcesem moglibyśmy wykonać trochę eksperymentów
praktycznych i przekonać się, że pomysł ten działa dla dowolnego
 Niech
Niech
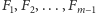 to zbiór fragmentów o maksymalnej
łącznej sumie, a
to zbiór fragmentów o maksymalnej
łącznej sumie, a
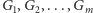 to pozostałe części tablicy (Rys. 3). Aby
uzyskać optymalne
to pozostałe części tablicy (Rys. 3). Aby
uzyskać optymalne
 fragmentów, albo dołączamy maksymalny
fragment, który jest zawarty w pewnym
fragmentów, albo dołączamy maksymalny
fragment, który jest zawarty w pewnym
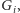 albo usuwamy minimalny
fragment z pewnego
albo usuwamy minimalny
fragment z pewnego
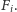 Zachęcamy do próby dowodu poprawności
tego rozwiązania. To może nie być proste, ale dla Czytelników Wytrwałych na
końcu artykułu podamy wskazówkę, jak można się do tego zabrać.
Zachęcamy do próby dowodu poprawności
tego rozwiązania. To może nie być proste, ale dla Czytelników Wytrwałych na
końcu artykułu podamy wskazówkę, jak można się do tego zabrać.
Pozostaje kwestia efektywnej implementacji tego pomysłu. Jedną fazę możemy
wykonać w czasie
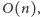 uruchamiając algorytm A2 na każdym
przedziale osobno. Tak zapisany algorytm A4 będzie działał w czasie
uruchamiając algorytm A2 na każdym
przedziale osobno. Tak zapisany algorytm A4 będzie działał w czasie
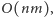 co nie daje nam jeszcze zysku w porównaniu z algorytmem A3.
Widać, że kluczową operacją jest odpowiadanie na pytania „jaki jest
maksymalny fragment w danym przedziale?” dla różnych przedziałów.
Pokażemy teraz, jak to robić efektywnie.
co nie daje nam jeszcze zysku w porównaniu z algorytmem A3.
Widać, że kluczową operacją jest odpowiadanie na pytania „jaki jest
maksymalny fragment w danym przedziale?” dla różnych przedziałów.
Pokażemy teraz, jak to robić efektywnie.
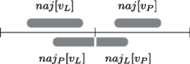
Rys. 4 Możliwe pozycje maksymalnego fragmentu
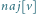 w zależności od
fragmentów w lewej i prawej połowie przedziału.
w zależności od
fragmentów w lewej i prawej połowie przedziału.
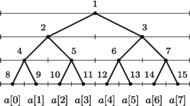
Rys. 5 Drzewo przedziałowe dla
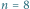 ma
ma
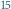 węzłów. Węzeł 5 odpowiada
przedziałowi bazowemu
węzłów. Węzeł 5 odpowiada
przedziałowi bazowemu
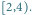 Przedział
Przedział
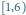 można podzielić na przedziały
bazowe, którym odpowiadają węzły 9, 5 i 6.
można podzielić na przedziały
bazowe, którym odpowiadają węzły 9, 5 i 6.
W tym celu może nam pomóc jeszcze jeden algorytm dla
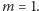 Algorytm
A5 będzie oparty o metodę „dziel i zwyciężaj”. Mając dany przedział
o długości
Algorytm
A5 będzie oparty o metodę „dziel i zwyciężaj”. Mając dany przedział
o długości
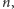 możemy go podzielić na dwie części o długości
możemy go podzielić na dwie części o długości
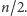 Maksymalny fragment w tym przedziale może znajdować się
w całości w lewej części, w całości w prawej części lub może składać się
z maksymalnego fragmentu, który dotyka prawej krawędzi lewej części, oraz
maksymalnego fragmentu, który dotyka lewej krawędzi prawej części (por. też
Rys. 4).
Maksymalny fragment w tym przedziale może znajdować się
w całości w lewej części, w całości w prawej części lub może składać się
z maksymalnego fragmentu, który dotyka prawej krawędzi lewej części, oraz
maksymalnego fragmentu, który dotyka lewej krawędzi prawej części (por. też
Rys. 4).
Załóżmy, że
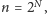 i zbudujmy drzewo przedziałowe (Rys. 5).
Drzewo będzie miało węzły o numerach od 1 do
i zbudujmy drzewo przedziałowe (Rys. 5).
Drzewo będzie miało węzły o numerach od 1 do
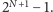 W węźle
W węźle
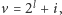 dla
dla
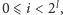 tego drzewa będą znajdować się informacje
o przedziale
tego drzewa będą znajdować się informacje
o przedziale
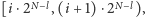 a konkretnie:
a konkretnie:
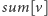 – suma
liczb w przedziale,
– suma
liczb w przedziale,
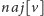 – maksymalny fragment w przedziale oraz
– maksymalny fragment w przedziale oraz
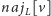 i
i
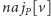 – maksymalne fragmenty dotykające odpowiednio
lewego i prawego końca przedziału. Wartości w węzłach najniższego poziomu
(tzn. dla
– maksymalne fragmenty dotykające odpowiednio
lewego i prawego końca przedziału. Wartości w węzłach najniższego poziomu
(tzn. dla
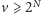 ) inicjujemy, przyjmując
) inicjujemy, przyjmując
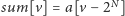 oraz
oraz
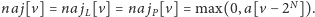 Wartości
w pozostałych węzłach
Wartości
w pozostałych węzłach
 wyznaczamy na podstawie wartości w węzłach
wyznaczamy na podstawie wartości w węzłach
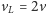 i
i
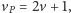 które odpowiadają lewej i prawej połowie
przedziału:
które odpowiadają lewej i prawej połowie
przedziału:

Wyznaczenie wartości we wszystkich węzłach zabiera czas
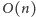 i w takim
czasie działa algorytm A5. Odpowiedzią jest, oczywiście, wartość
i w takim
czasie działa algorytm A5. Odpowiedzią jest, oczywiście, wartość
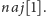
Skonstruowane drzewo przedziałowe wyróżnia się tym, że umożliwia ono
znalezienie największego fragmentu dla dowolnego przedziału tablicy w czasie
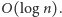 W tym celu przypomnijmy, że każdy przedział można
podzielić na
W tym celu przypomnijmy, że każdy przedział można
podzielić na
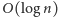 przedziałów bazowych, tzn. przedziałów,
które odpowiadają węzłom drzewa przedziałowego (Rys. 5). Niech
przedziałów bazowych, tzn. przedziałów,
które odpowiadają węzłom drzewa przedziałowego (Rys. 5). Niech
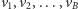 będą kolejnymi węzłami odpowiadającymi takiemu
podziałowi. Wtedy maksymalny fragment to będzie albo
będą kolejnymi węzłami odpowiadającymi takiemu
podziałowi. Wtedy maksymalny fragment to będzie albo
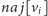 dla
pewnego
dla
pewnego
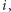 albo
albo
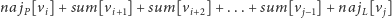 |
dla pewnych
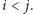
Poniższa pętla wyznacza maksymalny fragment
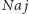 w czasie
w czasie
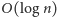 :
:

Algorytm A6 jest następujący: najpierw budujemy drzewo przedziałowe
(jak w algorytmie A5) oraz drugie drzewo przedziałowe, które będzie
liczyło minimalne fragmenty. Oprócz wartości
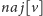 będziemy
potrzebować również końców fragmentów – odpowiednie wzbogacenie
drzewa przedziałowego zostawiamy jako ćwiczenie dla Czytelników.
Wszystkie przedziały trzymamy w kolejce priorytetowej: przedziały
będziemy
potrzebować również końców fragmentów – odpowiednie wzbogacenie
drzewa przedziałowego zostawiamy jako ćwiczenie dla Czytelników.
Wszystkie przedziały trzymamy w kolejce priorytetowej: przedziały
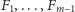 z priorytetami równymi minimalnym fragmentom w tych
przedziałach, zaś przedziały
z priorytetami równymi minimalnym fragmentom w tych
przedziałach, zaś przedziały
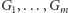 z priorytetami równymi
maksymalnym fragmentom.
z priorytetami równymi
maksymalnym fragmentom.
Każdy krok algorytmu to wyciągnięcie z kolejki przedziału o priorytecie
o największej wartości bezwzględnej, uaktualnienie wyniku o wartość
bezwzględną tego priorytetu, a następnie dodanie trzech nowych przedziałów
do kolejki. Cały algorytm działa w czasie
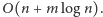

***
Algorytm A6 jest efektywny, ale dość skomplikowany w implementacji. Przedstawimy teraz prostszy (choć nieco zaskakujący) algorytm, na który autor artykułu wpadł, próbując udowodnić poprawność algorytmów A4 i A6. Algorytm ten korzysta z metody „spróbujmy to zrobić od końca”.
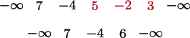
Rys. 6 Ciąg po podziale na bloki, powstały z tablicy liczb z rysunku 1, oraz ten sam ciąg po pierwszej fazie skracania.
Wypiszmy liczby z tablicy w ciągu i podzielmy go na maksymalne bloki liczb
o tym samym znaku (na potrzeby definicji bloku traktujemy 0 jako liczbę
dodatnią). Zauważmy, że w optymalnym rozwiązaniu każdy fragment musi
zaczynać się i kończyć pełnym blokiem, który zawiera liczby dodatnie
(jeśli kończyłby się niepełnym blokiem dodatnim, to moglibyśmy
ten fragment rozszerzyć, uzyskując nie gorsze rozwiązanie, a gdyby
kończył się blokiem ujemnym – moglibyśmy go skrócić). Możemy więc
zastąpić każdy blok przez jedną liczbę będącą sumą elementów tego bloku.
Dodatkowo dodajmy na obu końcach ciągu liczbę-strażnika
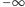 (Rys. 6).
(Rys. 6).
Jeśli w nowym ciągu mamy co najwyżej
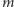 liczb dodatnich, to ich suma
jest rozwiązaniem zadania. W przeciwnym przypadku będziemy iteracyjnie
skracać ciąg, nie zmieniając optymalnego rozwiązania.
liczb dodatnich, to ich suma
jest rozwiązaniem zadania. W przeciwnym przypadku będziemy iteracyjnie
skracać ciąg, nie zmieniając optymalnego rozwiązania.
Faza skracania jest następująca: wybieramy liczbę w ciągu o najmniejszej wartości
bezwzględnej,
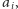 a następnie zastępujemy ją i dwie liczby z nią sąsiadujące
– ich sumą. Zauważmy, że nowa liczba
a następnie zastępujemy ją i dwie liczby z nią sąsiadujące
– ich sumą. Zauważmy, że nowa liczba
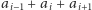 będzie miała
przeciwny znak do
będzie miała
przeciwny znak do
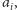 więc krótszy ciąg nadal będzie zawierał
naprzemiennie liczby dodatnie i ujemne. Fazę skracania można wykonać
w czasie
więc krótszy ciąg nadal będzie zawierał
naprzemiennie liczby dodatnie i ujemne. Fazę skracania można wykonać
w czasie
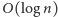 – wystarczy trzymać elementy ciągu na liście, a poza
tym mieć kolejkę priorytetową z liczbami uporządkowanymi względem ich
wartości bezwzględnych. Zatem algorytm A8 będzie działał w czasie
– wystarczy trzymać elementy ciągu na liście, a poza
tym mieć kolejkę priorytetową z liczbami uporządkowanymi względem ich
wartości bezwzględnych. Zatem algorytm A8 będzie działał w czasie
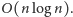
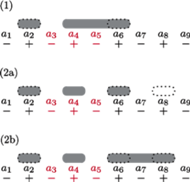
Rys. 7 Konstrukcja optymalnego rozwiązania niezawierającego wyróżnionych trzech liczb (linia przerywana) na podstawie dowolnego rozwiązania optymalnego niezawierającego którejś z tych liczb (szare obszary) dla przypadku dodatniej środkowej liczby.
Pozostaje udowodnić poprawność operacji skracania. Powiedzmy,
że ciąg składa się z 9 liczb oraz że liczbą o najmniejszej wartości
bezwzględnej jest
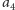 (dodatnia), więc chcemy skrócić ciąg, zastępując
(dodatnia), więc chcemy skrócić ciąg, zastępując
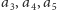 przez ich sumę (Rys. 7). Chcemy wykazać, że istnieje
optymalne rozwiązanie, w którym każdy fragment albo zawiera wszystkie
liczby
przez ich sumę (Rys. 7). Chcemy wykazać, że istnieje
optymalne rozwiązanie, w którym każdy fragment albo zawiera wszystkie
liczby
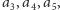 albo nie zawiera żadnej z nich. W tym celu pokażemy,
jak z rozwiązania optymalnego niespełniającego tego warunku skonstruować
rozwiązanie optymalne, które go spełnia. Rozważymy dwa przypadki:
albo nie zawiera żadnej z nich. W tym celu pokażemy,
jak z rozwiązania optymalnego niespełniającego tego warunku skonstruować
rozwiązanie optymalne, które go spełnia. Rozważymy dwa przypadki:
- (1) Rozwiązanie zawiera fragment, do którego
należą dwie spośród liczb
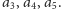 Wyrzucając z tego
fragmentu obie te liczby, dostaniemy nie gorsze rozwiązanie (bo
Wyrzucając z tego
fragmentu obie te liczby, dostaniemy nie gorsze rozwiązanie (bo
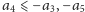 ).
).
- (2) Rozwiązanie zawiera jedną liczbę (czyli fragment
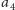 ).
Fragmentów jest mniej niż liczb dodatnich. Jeśli zatem
jakaś z liczb dodatnich (powiedzmy
).
Fragmentów jest mniej niż liczb dodatnich. Jeśli zatem
jakaś z liczb dodatnich (powiedzmy
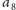 ) nie należy do
żadnego fragmentu, to zamieniając ją z
) nie należy do
żadnego fragmentu, to zamieniając ją z
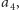 dostaniemy nie
gorsze rozwiązanie (bo
dostaniemy nie
gorsze rozwiązanie (bo
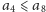 ). W przeciwnym przypadku
co najmniej jeden fragment zawiera więcej niż jedną liczbę
(powiedzmy
). W przeciwnym przypadku
co najmniej jeden fragment zawiera więcej niż jedną liczbę
(powiedzmy
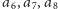 ). Możemy zatem wyrzucić z niego
jedną liczbę ujemną
). Możemy zatem wyrzucić z niego
jedną liczbę ujemną
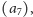 rozbijając go na dwa fragmenty.
Wyrzucając również fragment
rozbijając go na dwa fragmenty.
Wyrzucając również fragment
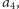 znowu dostaniemy nie
gorsze rozwiązanie (bo
znowu dostaniemy nie
gorsze rozwiązanie (bo
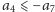 ).
).
Dowód, gdy liczba o najmniejszej wartości bezwzględnej jest ujemna, jest symetryczny i zostawiamy go jako ćwiczenie dla Czytelników.
I wreszcie nadszedł czas na obiecaną wskazówkę do dowodu poprawności
algorytmów A4 i A6. Wykonujmy kolejne fazy tych algorytmów, do momentu,
aż wszystkie fragmenty będą zawierać liczby o tych samych znakach.
Następnie wykonajmy na tak uzyskanym ciągu algorytm A8. Porównując
podział tablicy po
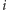 -tej fazie algorytmu A4 i przed
-tej fazie algorytmu A4 i przed
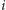 -tą od końca
fazą algorytmu A8, możemy dojść do wniosku, że w zasadzie te algorytmy
działają tak samo, tylko w odwrotnej kolejności. Szkoda, że na giełdzie nie
można najpierw sprzedać, a potem kupić...
-tą od końca
fazą algorytmu A8, możemy dojść do wniosku, że w zasadzie te algorytmy
działają tak samo, tylko w odwrotnej kolejności. Szkoda, że na giełdzie nie
można najpierw sprzedać, a potem kupić...
 dla
dla
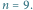 Optymalne rozwiązanie dla
Optymalne rozwiązanie dla
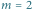 to
dwa zaznaczone fragmenty o sumach 7 i 6.
to
dwa zaznaczone fragmenty o sumach 7 i 6.
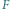 oraz fragmenty
oraz fragmenty
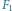 i
i
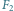 (szare obszary), jak również nowe rozwiązanie optymalne dla dwóch fragmentów
(przerywana linia).
(szare obszary), jak również nowe rozwiązanie optymalne dla dwóch fragmentów
(przerywana linia).
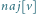 w zależności od
fragmentów w lewej i prawej połowie przedziału.
w zależności od
fragmentów w lewej i prawej połowie przedziału.
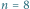 ma
ma
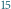 węzłów. Węzeł 5 odpowiada
przedziałowi bazowemu
węzłów. Węzeł 5 odpowiada
przedziałowi bazowemu
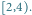 Przedział
Przedział
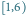 można podzielić na przedziały
bazowe, którym odpowiadają węzły 9, 5 i 6.
można podzielić na przedziały
bazowe, którym odpowiadają węzły 9, 5 i 6.