O sierotce, co chciała się mózgiem elektronowym wyręczyć
Wyobraźmy sobie biedną sierotkę, której macocha nakazała oddzielić groch od fasoli. Chcąc nie chcąc, dziewczę siada w kącie izby przed pokaźnym kopcem grochu pomieszanego z fasolą i zaczyna pracę. Praca jest niezwykle monotonna: sierotka bierze nasiono z górki i jeśli to fasola, odrzuca je na lewą stronę, a jeśli groch – na prawą; i tak w kółko...

Sierotka jest całkiem porządna, więc aby nie rzucać nasionkami po całej izbie, ustaliła, że nasionka fasoli odkłada na lewą stronę lewą ręką, a nasionka grochu odkłada prawą ręką. Ponieważ na wybór ręki, którą sięgnie po kolejne nasionko, musi się zdecydować, zanim rozpozna jego rodzaj (w izbie jest dość ciemno), więc nierzadko będzie zmuszona do przełożenia nasionka z jednej ręki do drugiej, co, oczywiście, będzie spowalniać jej pracę.
Powiedzmy, że sierotka w większości przypadków wyciąga z górki nasionko fasoli (takie już ma szczęście). Zauważywszy to, może postąpić praktycznie i na początku zawsze wyciągać nasionka lewą ręką, tak by zminimalizować liczbę przełożeń nasionka z ręki do ręki, a gdy w kopczyku zostanie już w większości groch, to będzie wyciągać nasionka prawą ręką. Sierotka może mieć szczęście innego rodzaju, np. prawie zawsze co trzecie wyciągnięte nasionko to groch. W tej sytuacji mądre dziewczę stwierdza, że najbardziej opłacalny jest schemat: lewa ręka, lewa ręka, prawa ręka itd. Niestety, znając bajkowe realia, sierotka najpewniej będzie wyciągała nasionka w zupełnie losowej kolejności, zatem żadne wymyślne strategie nie pomogą jej w uniknięciu marnego losu i średnio co drugie nasionko będzie musiało zostać przełożone z ręki do ręki.
Czytelnik Postępowy od razu zauważy, że wszystkie kłopoty skończyłyby się, gdyby na miejscu sierotki postawić robota z chwytnym ramieniem, fotokomórką i mózgiem elektronowym. Nie dość, że wykonałby on zadanie sprawniej i na pewno bezbłędnie, to nie rozwodziłby się długo nad wyborem strategii postępowania, a praca zajęłaby mu tyle samo czasu, niezależnie od kolejności, w jakiej wyciągałby ziarenka z górki.
I moglibyśmy zakończyć ten artykuł powyższym morałem, gdyby nie to, że nie jest on do końca prawdziwy. Okazuje się, że w świecie maszyn nie wszystko jest takie jasne i poukładane, a w elektronowym mózgu może kryć się coś ze sprytnej sierotki. Kto ciekaw, tego zapraszam do eksperymentu.
***
***
Ponieważ nie wszyscy Czytelnicy dysponują odpowiednim sprzętem tudzież
zapasem grochu i fasoli, więc eksperyment zasymulujemy na domowym
komputerze, pisząc prosty program. Program będzie wczytywał z wejścia
zero-jedynkowy ciąg, który kodować będzie rodzaje kolejnych nasionek.
Zamiast sortowania, program będzie miał na celu policzenie nasionek, tzn.
policzenie, ile zer i ile jedynek występuje w wejściowym ciągu. Jeśli te
wartości będzie przechowywał na zmiennych
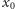 i
i
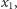 to po
każdorazowym wczytaniu nowego bitu
to po
każdorazowym wczytaniu nowego bitu
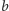 należy wykonać taki
kod:
należy wykonać taki
kod:

Skompilujmy nasz program i uruchommy go dla różnych ciągów
zero-jedynkowych równej długości, w których dokładnie połowa bitów to
zera. Wydawałoby się, że czas działania naszego programu musi być zawsze taki
sam, w końcu wykonamy dokładnie tyle samo operacji porównań
i dodawania, co więcej, wartości zmiennych
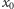 i
i
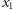 zwiększymy
tyle samo razy. Okazuje się jednak, że na moim komputerze dla ciągu
zwiększymy
tyle samo razy. Okazuje się jednak, że na moim komputerze dla ciągu
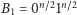 długości
długości
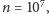 w którym pierwsza połowa ciągu
to zera, a druga połowa to jedynki, program działa
w którym pierwsza połowa ciągu
to zera, a druga połowa to jedynki, program działa
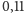 s, natomiast dla
ciągu
s, natomiast dla
ciągu
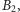 w którym pozycje zer i jedynek są losowe, program działa
w którym pozycje zer i jedynek są losowe, program działa
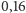 s, czyli prawie o połowę dłużej! Nie jest to bynajmniej błąd pomiaru
czasu, gdyż kolejne uruchomienia programu potwierdzają pierwotną
obserwację. Ponadto w obu uruchomieniach programu wczytywanie danych
zajmuje
s, czyli prawie o połowę dłużej! Nie jest to bynajmniej błąd pomiaru
czasu, gdyż kolejne uruchomienia programu potwierdzają pierwotną
obserwację. Ponadto w obu uruchomieniach programu wczytywanie danych
zajmuje
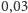 s, więc dysproporcja czasu „właściwych obliczeń” jest
w rzeczywistości jeszcze większa.
s, więc dysproporcja czasu „właściwych obliczeń” jest
w rzeczywistości jeszcze większa.
Jaka jest przyczyna takiego zachowania? Czyżby domowy komputer z jakichś powodów radził sobie lepiej z „przewidywalnymi” danymi, tak jak nasza sierotka? A jeśli tak jest w istocie, to jakie są tego powody?
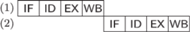
Rys. 1 Na wykonanie instrukcji procesora składają się cztery kroki: IF (ang. instruction fetch), ID
(instruction decode), EX (execute), WB (write back). Na wykonanie dwóch instrukcji
potrzebujemy
 jednostek czasu.
jednostek czasu.
Jak wiemy, kompilacja powoduje przetworzenie kodu programu na ciąg instrukcji
niskiego poziomu. Na przykład, zwiększenie wartości zmiennej znajdującej się
w rejestrze
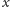 procesora mogłoby zostać zapisane w wewnętrznym
języku komputera jako
procesora mogłoby zostać zapisane w wewnętrznym
języku komputera jako

Na wykonanie powyższej instrukcji składa się kilka kroków. Po pierwsze,
instrukcja musi być pobrana z pamięci. Następnie musi zostać zdekodowana:
procesor odkrywa, że chodzi o zwiększenie zmiennej z rejestru. W kolejnym
kroku należy wykonać instrukcję: przesłać wartość zmiennej z rejestru do
jednostki arytmetycznej procesora i dokonać zwiększenia. I ostatecznie należy
przesłać uaktualnioną wartość z powrotem do rejestru. (Jest to przykład
dość uproszczony, w ogólnym przypadku wykonanie instrukcji może
składać się z większej liczby kroków, tj. np. przekopiowanie danych z pamięci
do rejestru procesora. We współczesnych procesorach liczba takich kroków
może sięgać kilkudziesięciu.) Widać więc, że wykonanie pojedynczej
instrukcji nie jest takie banalne. Jeśli założymy, że każdy krok wykonuje się
w jednej jednostce czasu, to na wykonanie
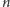 instrukcji potrzebujemy
instrukcji potrzebujemy
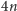 jednostek czasu (Rys. 1).
jednostek czasu (Rys. 1).
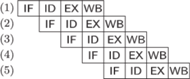
Rys. 2 Dzięki przetwarzaniu potokowemu (ang. pipelining) w
 jednostkach czasu
jesteśmy w stanie wykonać
jednostkach czasu
jesteśmy w stanie wykonać
 instrukcji w przypadku pustego potoku i aż
instrukcji w przypadku pustego potoku i aż
 instrukcji w przypadku wypełnionego potoku.
instrukcji w przypadku wypełnionego potoku.
Zauważmy jednak, że skoro każdy z kroków jest wykonywany przez inną
część procesora, to można przyspieszyć cały proces, umożliwiając tym
częściom procesora pracę równoległą przez przetwarzanie kilku instrukcji
naraz. (Tak jak na linii produkcyjnej w fabryce samochodów ekipa montująca
podwozie pracuje równolegle z ekipą malującą karoserię – pracują po prostu na
innych egzemplarzach.) Można postąpić tak: w pierwszym kroku pobieramy
pierwszą instrukcję z pamięci. W drugim kroku dekodujemy tę instrukcję, ale
w tym momencie część procesora odpowiedzialna za pobieranie instrukcji jest
bezrobotna, wobec tego możemy jednocześnie pobrać z pamięci
drugą instrukcję. W trzecim kroku wykonujemy pierwszą instrukcję,
dekodujemy drugą i pobieramy z pamięci trzecią. Dzięki takiemu potokowemu
przetwarzaniu instrukcji na wykonanie
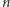 z nich potrzebujemy tylko
z nich potrzebujemy tylko
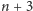 jednostek czasu (Rys. 2).
jednostek czasu (Rys. 2).
Jak każdy świetny pomysł, tak i ten ma pewne wady. Zauważmy, że przyjęliśmy tu milczące założenie, że zanim zakończymy wykonywanie danej instrukcji, musimy być w stanie rozpocząć wykonywanie następnej, a nawet trzeciej instrukcji z kolei. W szczególności musimy wiedzieć, co to będą za instrukcje. O tym, że nie zawsze posiadamy tę wiedzę, możemy się przekonać, kompilując nasz pierwszy program:

W pierwszej instrukcji zapisanej pod adresem
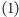 wykonujemy
porównanie zmiennej
wykonujemy
porównanie zmiennej
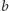 z zerem. Następna instrukcja jest instrukcją
skoku warunkowego: jeśli liczby porównywane ostatnio były równe,
to instrukcja ta powoduje skok do instrukcji zapisanej pod adresem
z zerem. Następna instrukcja jest instrukcją
skoku warunkowego: jeśli liczby porównywane ostatnio były równe,
to instrukcja ta powoduje skok do instrukcji zapisanej pod adresem
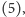 w przeciwnym przypadku nie dzieje się nic. Odpowiada to wybraniu
odpowiedniej gałęzi w instrukcji if. Jeśli wykonaliśmy skok (pierwsza gałąź),
to w instrukcji
w przeciwnym przypadku nie dzieje się nic. Odpowiada to wybraniu
odpowiedniej gałęzi w instrukcji if. Jeśli wykonaliśmy skok (pierwsza gałąź),
to w instrukcji
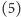 zwiększamy wartość
zwiększamy wartość
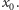 Jeśli skoku nie
wykonaliśmy (druga gałąź), to w instrukcji
Jeśli skoku nie
wykonaliśmy (druga gałąź), to w instrukcji
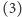 zwiększamy wartość
zwiększamy wartość
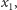 a następnie wykonujemy bezwarunkowy skok do instrukcji
a następnie wykonujemy bezwarunkowy skok do instrukcji
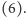 Kluczowa jest w tym programie instrukcja skoku warunkowego
IFEQJMP: mianowicie, dopóki jej nie wykonamy, nie wiemy, czy następną po niej
będzie instrukcja
Kluczowa jest w tym programie instrukcja skoku warunkowego
IFEQJMP: mianowicie, dopóki jej nie wykonamy, nie wiemy, czy następną po niej
będzie instrukcja
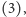 czy też instrukcja
czy też instrukcja
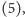 nie wiemy więc,
która z nich powinna być w potoku uwzględniona jako następna. Procesor jest
zatem w sytuacji naszej sierotki, która, dopóki nie dotknie nowego
ziarenka, nie będzie wiedziała, czy należało użyć lewej czy też prawej
ręki.
nie wiemy więc,
która z nich powinna być w potoku uwzględniona jako następna. Procesor jest
zatem w sytuacji naszej sierotki, która, dopóki nie dotknie nowego
ziarenka, nie będzie wiedziała, czy należało użyć lewej czy też prawej
ręki.
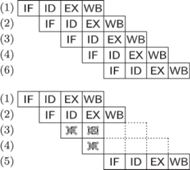
Rys. 3 Sytuacja w potoku w przypadku, gdy skok warunkowy w instrukcji
 nie
nastąpił i gdy nastąpił. Liczby w nawiasach oznaczają numery instrukcji; w pierwszym
przypadku w instrukcji (4) występuje bezwarunkowy skok do instrukcji (6).
nie
nastąpił i gdy nastąpił. Liczby w nawiasach oznaczają numery instrukcji; w pierwszym
przypadku w instrukcji (4) występuje bezwarunkowy skok do instrukcji (6).
Można ten kłopot spróbować rozwiązać następująco: procesor zawsze będzie
zakładał, że po instrukcji zapisanej pod adresem
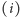 następują instrukcje
pod adresami
następują instrukcje
pod adresami
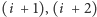 itd. lub pod adresem, który wskazuje skok
bezwarunkowy, i te właśnie instrukcje będzie uwzględniał w potoku. Jeśli
jednak instrukcja
itd. lub pod adresem, który wskazuje skok
bezwarunkowy, i te właśnie instrukcje będzie uwzględniał w potoku. Jeśli
jednak instrukcja
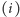 była rozkazem warunkowego skoku i po jej
wykonaniu okazało się, że należy skoczyć pod adres
była rozkazem warunkowego skoku i po jej
wykonaniu okazało się, że należy skoczyć pod adres
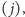 to częściowa
praca związana z wykonaniem instrukcji
to częściowa
praca związana z wykonaniem instrukcji
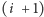 i kolejnych jest
unieważniana, a potok jest opróżniany i przetwarzanie zaczyna się na nowo
od instrukcji
i kolejnych jest
unieważniana, a potok jest opróżniany i przetwarzanie zaczyna się na nowo
od instrukcji
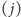 (Rys. 3).
(Rys. 3).
W przypadku programów, w których jest mało skoków warunkowych
lub są rzadko wykonywane, taka strategia może się opłacać. Jednak
w pesymistycznym przypadku, gdy każda kolejna instrukcja jest skokiem
warunkowym, musimy opróżniać potok po wykonaniu każdej instrukcji,
zatem czas wykonania
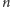 instrukcji będzie wynosił
instrukcji będzie wynosił
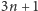 jednostek
– nasz potok nie będzie zatem wykorzystywany w pełni efektywnie.
jednostek
– nasz potok nie będzie zatem wykorzystywany w pełni efektywnie.
Zauważmy jednak, że taka strategia nie może być stosowana w naszym
procesorze: przecież program dla ciągów
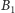 i
i
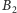 powinien
działać tak samo długo, gdyż w obu przypadkach potok byłby opróżniany
w połowie instrukcji
powinien
działać tak samo długo, gdyż w obu przypadkach potok byłby opróżniany
w połowie instrukcji
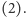 Taka strategia odpowiada sytuacji, w której
nasza sierotka postanowiłaby zawsze używać lewej ręki.
Taka strategia odpowiada sytuacji, w której
nasza sierotka postanowiłaby zawsze używać lewej ręki.
Możemy przyjąć inną metodę postępowania i próbować zgadnąć, czy dany skok warunkowy będzie wykonany, czy też nie. Okazuje się, że współczesne procesory tak właśnie postępują. Co więcej, ponieważ nie znają przyszłości, więc zachowują się jak nasza sierotka i zakładają, że będą miały szczęście i na podstawie zachowań instrukcji skoku warunkowego w przeszłości będą w stanie przewidzieć, jak będzie się ona zachowywała w przyszłości.
Zapiszmy historię wykonywania skoku warunkowego w postaci ciągu
złożonego z liter T i N. Jedna z najprostszych strategii zgadywania jest
następująca: przyjmujemy, że skok będzie wykonany, jeśli ostatnim
razem był wykonany (czyli ostatnia litera w ciągu to T). Ta strategia ma
sens w przypadku długich sekwencji analogicznych wyborów, jak to
ma miejsce dla ciągu
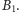 Można ją trochę ulepszyć, aby była
niewrażliwa na sporadyczne przekłamania w historii, za pomocą wskaźnika
mogącego przyjmować cztery stany:
Można ją trochę ulepszyć, aby była
niewrażliwa na sporadyczne przekłamania w historii, za pomocą wskaźnika
mogącego przyjmować cztery stany:
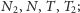 każde wykonanie
skoku powoduje zmianę stanu wskaźnika o jeden w prawo zgodnie
z rysunkiem 4, a niewykonanie skoku – w lewo. Zgadujemy, że skok
zostanie wykonany, jeśli wskaźnik znajduje się w stanie
każde wykonanie
skoku powoduje zmianę stanu wskaźnika o jeden w prawo zgodnie
z rysunkiem 4, a niewykonanie skoku – w lewo. Zgadujemy, że skok
zostanie wykonany, jeśli wskaźnik znajduje się w stanie
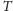 lub
lub
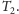
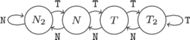
Rys. 4 Czterostanowy wskaźnik zgadujący, czy skok zostanie wykonany.
Gdyby w naszym procesorze zastosowano powyższą strategię, wyjaśniałaby
ona różnice w działaniu programu dla ciągów
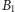 i
i
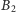 :
w przypadku pierwszego z nich nasza strategia zgadywania nie zadziała tylko
kilka razy (w środku ciągu i, być może, na początku), z kolei jest ona
zupełnie bezużyteczna (jak w zasadzie jakakolwiek strategia zgadywania)
w przypadku drugiego z nich.
:
w przypadku pierwszego z nich nasza strategia zgadywania nie zadziała tylko
kilka razy (w środku ciągu i, być może, na początku), z kolei jest ona
zupełnie bezużyteczna (jak w zasadzie jakakolwiek strategia zgadywania)
w przypadku drugiego z nich.
Niestety, to nie wyjaśnia, dlaczego dla ciągu
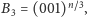 w którym
dokładnie co trzeci bit to
w którym
dokładnie co trzeci bit to
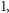 czas działania jest taki sam jak dla ciągu
czas działania jest taki sam jak dla ciągu
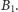 Wszak dla ciągu
Wszak dla ciągu
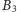 musielibyśmy pomylić się dla każdej
jedynki, czyli co najmniej
musielibyśmy pomylić się dla każdej
jedynki, czyli co najmniej
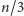 razy. Okazuje się, że strategia stosowana
przez współczesne procesory próbuje uwzględniać możliwość wystąpienia
krótkich cykli w historii wykonywania skoku i jest z tego powodu trochę
bardziej skomplikowana. Mianowicie, przy podejmowaniu decyzji patrzymy na
razy. Okazuje się, że strategia stosowana
przez współczesne procesory próbuje uwzględniać możliwość wystąpienia
krótkich cykli w historii wykonywania skoku i jest z tego powodu trochę
bardziej skomplikowana. Mianowicie, przy podejmowaniu decyzji patrzymy na
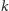 ostatnich liter w historii i na podstawie tych liter wybieramy
jeden z
ostatnich liter w historii i na podstawie tych liter wybieramy
jeden z
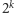 czterostanowych wskaźników, który uaktualniamy
i podejmujemy decyzję zgodnie z jego wskazaniem. W ten sposób dostajemy
mechanizm, który będzie zgadywał poprawnie, o ile w historii wykonywania
skoku każde
czterostanowych wskaźników, który uaktualniamy
i podejmujemy decyzję zgodnie z jego wskazaniem. W ten sposób dostajemy
mechanizm, który będzie zgadywał poprawnie, o ile w historii wykonywania
skoku każde
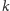 kolejnych bitów jednoznacznie wyznacza bit
kolejnych bitów jednoznacznie wyznacza bit
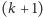 -szy. W moim komputerze jest
-szy. W moim komputerze jest
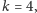 zatem w ciągu
zatem w ciągu
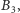 którego historię można opisać regułami: po każdym TT jest
N, po każdym TN jest T, a po każdym NT jest T, procesor nie pomyli
się ani razu (z wyłączeniem kilku potencjalnych pomyłek na początku
ciągu).
którego historię można opisać regułami: po każdym TT jest
N, po każdym TN jest T, a po każdym NT jest T, procesor nie pomyli
się ani razu (z wyłączeniem kilku potencjalnych pomyłek na początku
ciągu).
Opisane strategie nie są jedynymi, które są stosowane we współczesnych procesorach. Istnieje cała gama rozwiązań, które pozwalają przewidywać typowe historie wykonywania skoku. W niektórych procesorach do problemu podchodzi się zupełnie inaczej. Zakłada się, na przykład, że w skompilowanym kodzie po każdej instrukcji skoku warunkowego musi wystąpić pewna liczba zwykłych instrukcji, które będą wykonane niezależnie od tego, czy skok nastąpi, czy nie, aby po ich wykonaniu adres docelowy był już obliczony.
***
***
Morał z tej bajki jest taki, że nawet kolejność, w jakiej podajemy dane programowi komputerowemu, ma znaczenie (mimo że na pierwszy rzut oka może wydawać się to niewiarygodne). Drugi morał jest ważną wskazówką dla programisty: w kodzie, w którym ważna jest efektywność wykonania, należy, o ile to możliwe, unikać skoków. Okazuje się, że nasz pierwszy program możemy przepisać tak, by nie występowała w nim instrukcja if:

Tak napisany program działa w czasie
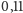 s dla każdego z ciągów
s dla każdego z ciągów
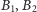 i
i
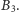
 jednostek czasu.
jednostek czasu.
 jednostkach czasu
jesteśmy w stanie wykonać
jednostkach czasu
jesteśmy w stanie wykonać
 instrukcji w przypadku pustego potoku i aż
instrukcji w przypadku pustego potoku i aż
 instrukcji w przypadku wypełnionego potoku.
instrukcji w przypadku wypełnionego potoku.
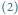 nie
nastąpił i gdy nastąpił. Liczby w nawiasach oznaczają numery instrukcji; w pierwszym
przypadku w instrukcji (4) występuje bezwarunkowy skok do instrukcji (6).
nie
nastąpił i gdy nastąpił. Liczby w nawiasach oznaczają numery instrukcji; w pierwszym
przypadku w instrukcji (4) występuje bezwarunkowy skok do instrukcji (6).