Czy
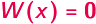 ?
?
Poszukiwanie pierwiastków wielomianu jest jednym z podstawowych zagadnień rozważanych we wszystkich naukach ścisłych. W tym artykule zajmiemy się czymś znacznie prostszym: sprawdzaniem, czy dana liczba jest pierwiastkiem zadanego wielomianu.
Mając dany wielomian
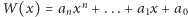 i konkretną wartość
parametru
i konkretną wartość
parametru
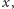 chcemy więc sprawdzić, czy
chcemy więc sprawdzić, czy
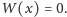 Można by
spytać, czy nie wystarczy w tym celu podstawić wartość
Można by
spytać, czy nie wystarczy w tym celu podstawić wartość
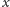 i na tym
skończyć? Rzeczywiście, jeśli mamy do czynienia z „nieskomplikowanym”
wielomianem (cokolwiek by to miało znaczyć) i „sensownym” parametrem
i na tym
skończyć? Rzeczywiście, jeśli mamy do czynienia z „nieskomplikowanym”
wielomianem (cokolwiek by to miało znaczyć) i „sensownym” parametrem
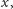 to problem jest trywialny. Może się jednak okazać, że nasze dane
nie są „nieskomplikowane i sensowne”, ale za to możemy wesprzeć się
domowym komputerem...
to problem jest trywialny. Może się jednak okazać, że nasze dane
nie są „nieskomplikowane i sensowne”, ale za to możemy wesprzeć się
domowym komputerem...
Przede wszystkim należy sprecyzować, jakimi liczbami zamierzamy
się zajmować. Aha, a więc to tutaj tkwi haczyk! Podejrzliwy Czytelnik
zapewne domyśla się już, że za moment wkroczymy w mroczny świat
komputerowych reprezentacji liczb rzeczywistych, z przybliżeniami,
cechami, mantysami i wszędobylskimi epsilonami. Faktycznie, komputerowe
sprawdzenie równości
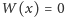 w liczbach rzeczywistych
nastręcza pewnych trudności i jest istotnym zagadnieniem w dziedzinie
metod numerycznych. My jednak nie będziemy się w to tutaj wgłębiać
i założymy, że mamy do czynienia wyłącznie z liczbami całkowitymi.
Czy w takim razie problem zawiera w sobie jeszcze jakąś trudność?
Owszem.
w liczbach rzeczywistych
nastręcza pewnych trudności i jest istotnym zagadnieniem w dziedzinie
metod numerycznych. My jednak nie będziemy się w to tutaj wgłębiać
i założymy, że mamy do czynienia wyłącznie z liczbami całkowitymi.
Czy w takim razie problem zawiera w sobie jeszcze jakąś trudność?
Owszem.
Otóż nieprzyjemne jest to, że przy obliczaniu
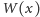 szybko zaczynamy
mieć do czynienia z bardzo dużymi liczbami. I to nawet wtedy, gdy
współczynniki
szybko zaczynamy
mieć do czynienia z bardzo dużymi liczbami. I to nawet wtedy, gdy
współczynniki
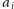 są niewielkie, co dla informatyka znaczy, że co do
wartości bezwzględnej nie przekraczają dwóch miliardów (orientacyjne
ograniczenie standardowego typu całkowitego 32-bitowego ze znakiem;
faktycznie jest to
są niewielkie, co dla informatyka znaczy, że co do
wartości bezwzględnej nie przekraczają dwóch miliardów (orientacyjne
ograniczenie standardowego typu całkowitego 32-bitowego ze znakiem;
faktycznie jest to
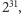 czyli trochę więcej). Rzeczywiście, bez trudu
widzimy, że jednym z pierwiastków wielomianu:
czyli trochę więcej). Rzeczywiście, bez trudu
widzimy, że jednym z pierwiastków wielomianu:

jest
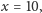 ale jeśli chcielibyśmy to sprawdzić, wykonując
proste podstawienie, musielibyśmy operować na liczbach zawierających
1000 cyfr. Nawet osoba niezaznajomiona z komputerem łatwo zauważy,
że obliczenia na takich długaśnych liczbach muszą być w jakimś
sensie trudniejsze. Tak jest w istocie: wykonywanie operacji na dużych
liczbach jest powolne, a do tego bywa wyjątkowo niewygodne, jeśli
akurat natrafimy na system czy język programowania, który dostarcza
implementacje działań jedynie na wbudowanych typach całkowitych, co
zazwyczaj oznacza liczby 64-bitowe (ze znakiem), czyli mniejsze co do
wartości bezwzględnej niż
ale jeśli chcielibyśmy to sprawdzić, wykonując
proste podstawienie, musielibyśmy operować na liczbach zawierających
1000 cyfr. Nawet osoba niezaznajomiona z komputerem łatwo zauważy,
że obliczenia na takich długaśnych liczbach muszą być w jakimś
sensie trudniejsze. Tak jest w istocie: wykonywanie operacji na dużych
liczbach jest powolne, a do tego bywa wyjątkowo niewygodne, jeśli
akurat natrafimy na system czy język programowania, który dostarcza
implementacje działań jedynie na wbudowanych typach całkowitych, co
zazwyczaj oznacza liczby 64-bitowe (ze znakiem), czyli mniejsze co do
wartości bezwzględnej niż
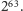 No dobrze, ale my chcemy tylko
sprawdzić, czy
No dobrze, ale my chcemy tylko
sprawdzić, czy
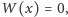 a niekoniecznie od razu obliczyć
dokładną wartość
a niekoniecznie od razu obliczyć
dokładną wartość
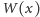 – to przecież musi być prostsze!
I rzeczywiście: poniżej opisujemy krótką i elegancką metodę rozwiązującą
ten problem.
– to przecież musi być prostsze!
I rzeczywiście: poniżej opisujemy krótką i elegancką metodę rozwiązującą
ten problem.
Załóżmy, że
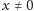 – z przypadkiem
– z przypadkiem
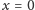 łatwo sobie
poradzić, sprawdzając, czy
łatwo sobie
poradzić, sprawdzając, czy
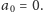 Chcemy stwierdzić, czy:
Chcemy stwierdzić, czy:

równoważnie czy:

Lewa strona jest podzielna przez
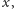 a zatem prawa też musi dzielić się
przez
a zatem prawa też musi dzielić się
przez
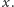 Otrzymujemy pierwszy warunek konieczny na to, żeby
Otrzymujemy pierwszy warunek konieczny na to, żeby
 było pierwiastkiem
było pierwiastkiem
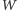 :
:
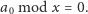 | (1) |
Jeśli on zachodzi, możemy całą równość podzielić przez
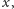 otrzymując:
otrzymując:

Ta sytuacja jest podobna do poprzedniej. Przerzucamy
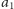 na drugą
stronę:
na drugą
stronę:

i otrzymujemy drugi warunek konieczny:
 | (2) |
Następnie znów dzielimy obie strony równości przez
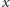 i kontynuujemy
to postępowanie, aż po lewej stronie pozostanie samo
i kontynuujemy
to postępowanie, aż po lewej stronie pozostanie samo
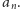 Po drodze
otrzymamy kolejne warunki konieczne na to, żeby
Po drodze
otrzymamy kolejne warunki konieczne na to, żeby
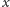 było pierwiastkiem
wielomianu
było pierwiastkiem
wielomianu
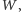 na przykład trzeci z nich będzie postaci:
na przykład trzeci z nich będzie postaci:
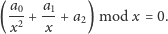 | (3) |
Na końcu zaś wystarczy sprawdzić, czy:
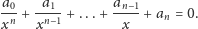 | (4) |
W ten sposób uzyskujemy następujący pseudokod, w którym sprawdzamy kolejno warunki (1), (2), (3) itd., a na końcu (4).

Zauważmy, że wartość zmiennej
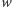 nigdy nie przekroczy sumy
wartości bezwzględnych liczb
nigdy nie przekroczy sumy
wartości bezwzględnych liczb
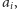 więc nie będziemy mieć do czynienia
z żadnymi dużymi liczbami. Czyli pełny sukces!
więc nie będziemy mieć do czynienia
z żadnymi dużymi liczbami. Czyli pełny sukces!
Na zakończenie warto dodać, że podany problem można także rozwiązać za pomocą tak zwanego schematu Hornera, w którym wykorzystujemy następujące przedstawienie:

Wystarczy mianowicie próbować obliczyć
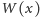 zgodnie
z tym schematem, od lewej do prawej – na przemian mnożymy przez
zgodnie
z tym schematem, od lewej do prawej – na przemian mnożymy przez
 i dodajemy
i dodajemy
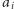 – przy czym obliczenia przerywamy, jeśli
aktualna wartość staje się zbyt duża. Wiemy wówczas, że na pewno
wynikiem nie będzie zero. A to, jaka jest ta graniczna wartość, przy której
możemy od razu udzielić odpowiedzi negatywnej, pozostawiamy do
rozstrzygnięcia Czytelnikowi.
– przy czym obliczenia przerywamy, jeśli
aktualna wartość staje się zbyt duża. Wiemy wówczas, że na pewno
wynikiem nie będzie zero. A to, jaka jest ta graniczna wartość, przy której
możemy od razu udzielić odpowiedzi negatywnej, pozostawiamy do
rozstrzygnięcia Czytelnikowi.