Dźwięk możemy zobaczyć: wystarczy spojrzeć na wykres amplitudy fali akustycznej. Fala ta jest sumą składowych o różnych częstotliwościach. Idealny ton obrazuje sinusoidalny wykres o odpowiedniej częstotliwości. Np. dźwiękowi A4 we współczesnym 88-klawiszowym fortepianie odpowiada ton o częstotliwości 440 Hz. Względem tej wartości liczone są częstotliwości tonów odpowiadających dźwiękom wszystkich klawiszy: 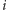-temu klawiszowi odpowiada częstotliwość

zatem dźwiękowi C3 (który jest dźwiękiem 28. klawisza) odpowiada częstotliwość 130,813 Hz. Na rysunku 1 przedstawiony został fragment wykresu fali dźwiękowej dla idealnego tonu tej częstotliwości. Poniżej na rysunku przedstawiono wykres fali dla rzeczywistego dźwięku C3 fortepianu – zawiera on więcej składowych harmonicznych, ale najniższa częstotliwość jest zachowana. Im bardziej skomplikowany jest dźwięk, tym więcej zawiera składowych harmonicznych.

Zapis w formacie cyfrowym

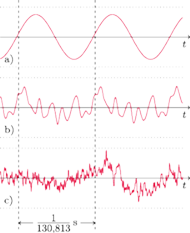
Rys. 1 Wykres amplitudy dwóch fal dźwiękowych o częstotliwości 130,813 Hz:
a) idealnej sinusoidalnej,
b) fortepianu,
c) wykres fragmentu piosenki.
Po przekształceniu do formatu LPCM każdy z tych fragmentów zostanie zakodowany w 800 próbkach.

Ponieważ na płycie CD zapisujemy sygnał (opis fali dźwiękowej) w postaci zero-jedynkowej, musimy najpierw przekształcić go z postaci analogowej. Robimy to metodą LPCM (ang. linear pulse-code modulation), która przebiega dwutorowo: po pierwsze, nie zapiszemy wartości sygnału dla każdej chwili, a jedynie dla wybranych w równych odstępach chwil; taki proces nazywamy próbkowaniem. Po drugie, możemy zapisać tylko skończoną liczbę wartości sygnału, zatem dokonamy kwantyzacji. Pozostaje wobec powyższego ustalenie częstotliwości próbkowania i sposobu kwantyzacji.

Człowiek słyszy dźwięki w zakresie częstotliwości od 12 Hz do 20 kHz (zatem zakres fortepianu – od 27,5 Hz do 4186 Hz – jest dla niego dostępny). Zgodnie z twierdzeniem Nyquista–Shannona, aby móc prawidłowo odtworzyć sygnał ciągły z dyskretnego ciągu próbek, należy próbkować z częstotliwością co najmniej dwa razy większą od największej częstotliwości występującej w sygnale. Z tego powodu przyjęto, że sygnał przed cyfryzacją zostanie poddany działaniu filtra dolnoprzepustowego, który obetnie częstotliwości wyższe niż 22 kHz (i tak ich nie usłyszymy), a następnie zostanie spróbkowany z częstotliwością 44,1 kHz (dokładna wartość ma uzasadnienie historyczne).

Co do kwantyzacji, przyjęto, że pojedyncza próbka będzie zapisana na 16 bitach (2 bajtach), co daje 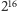 poziomów. W metodzie LPCM po prostu liniowo przekształcamy przedział wartości sygnału na dostępny zakres poziomów (u nas od 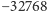 do ).

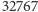Ile potrzeba na to miejsca?

Otóż płyta CD jest wrażliwa na zarysowania powierzchni, które mogą skutkować błędnym odczytem. Dlatego też sygnał zapisuje się z użyciem kodowania umożliwiającego wychwytywanie błędów odczytu. W przypadku wykrycia poważnego błędu na płycie audio stosuje się metody bazujące na interpolacji wartości sąsiednich próbek. Jest to rozsądne rozwiązanie dla sygnału dźwiękowego (i tak nie usłyszymy ewentualnej różnicy), jednak niedopuszczalne w przypadku płyty z danymi. Dlatego na takich płytach wprowadza się dodatkową warstwę synchronizacji i korekcji, która zajmuje 304 bity na każde 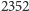 bitów. 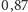Powoduje to, że na płycie z danymi zapiszemy około  raza mniej niż na płycie audio.

Morał z tego jest taki, że o ile zrobienie kopii płyty z danymi powinno udać się nawet dla dość porysowanych płyt, to idealne skopiowanie zawartości płyty audio (np. w celu słuchania muzyki z komputera) nierzadko przysparza kłopotów. Jeśli podczas odtwarzania skopiowanych piosenek słyszymy zacięcia lub trzaski, warto skorzystać z programów do tworzenia wiernych kopii, takich jak cdparanoia lub Exact Audio Copy.

Wojna na decybele

Możemy podejrzeć, jak wygląda wykres fali dźwiękowej dla skopiowanej na komputer piosenki, np. używając programu Audacity. Na rysunku 2 przedstawiony został fragment piosenki – górny wykres to oryginał z roku 1988, natomiast dolny to wersja z albumu z roku 1995 będącego kompilacją wybranych utworów zespołu. Piosenka jest ta sama, jednak wykresy są inne – na drugim albumie piosenka jest po prostu nagrana głośniej. Jest to efekt niedobrej tendencji, nasilającej się od lat 90., a wiążącej się z przekonaniem, że im coś głośniejsze, tym bardziej nam się podoba. Skutkuje to tym, że producenci muzyczni chcą, by to właśnie ich nagrania wybijały się z tłumu, czyli były jak najgłośniejsze; ich starania określa się jako tzw.  loudness war. Niestety, zakres poziomów dostępnych na płycie CD jest ustalony i nie da się go obejść, chyba że zacznie się manipulować dźwiękiem.

Rys. 2 Pierwsze 13 sekund piosenki The Look zespołu Roxette z płyty a) Look Sharp! (rok 1988) i b) Don’t Bore Us (rok 1995).

Jeśli przyjrzymy się górnemu wykresowi, to dostrzeżemy, że pik w okolicach 8 s osiąga prawie maksymalną wartość. Wynika z tego, że głośność tego nagrania można zwiększyć bardzo nieznacznie, a jednak początkowy fragment dolnego wykresu ma 2 razy większą amplitudę niż odpowiadający mu fragment na górnym wykresie! Widać zatem, że dźwięk na drugim albumie jest zniekształcony w stosunku do oryginału. Takie zniekształcenie, które ma sprawić, by dźwięk wydawał nam się głośniejszy, można zrealizować na wiele sposobów.

Można np. nierównomiernie zwiększyć głośność muzyki – im cichszy jest dany fragment, tym bardziej zwiększamy jego głośność. To powoduje, że zakres dynamiczny (ang. dynamic range) piosenki (czyli różnica między głośnością najcichszego i najgłośniejszego fragmentu) jest mniejszy, a muzyka staje się monotonna. (Swoją drogą, niestety, jest to zaleta, jeśli słuchamy nagrania na kiepskim sprzęcie i w hałaśliwym miejscu, np. podczas jazdy samochodem.)

Rys. 3 Fragment piosenki Stars (300 próbek; okolice 210,5 s) z albumu Have a Nice Day (rok 1999) grupy Roxette.

Drugi sposób jest bardziej brutalny, gdyż nieodwracalnie niszczy fragmenty dźwięku: można po prostu obciąć wartości, które po zwiększeniu amplitudy przekroczyły dostępny zakres. Na rysunku 3 pokazano, jak to wygląda w praktyce – obcięty fragment ma długość aż 85 próbek.

Co dalej?

Jeśli chcielibyśmy zarchiwizować naszą kolekcję płyt CD na komputerze, to na każdą płytę musimy liczyć średnio 650 MB, co np. dla 20 płyt daje 13 GB. Trochę dużo. Warto zatem zapisać nasze piosenki w formacie, który wspiera kompresję dźwięku. Ale to temat na osobny artykuł.