Rozważmy następujący program będący tabliczką mnożenia. To, w jakiej kolejności będziemy obliczać poszczególne wartości, nie powinno mieć w sumie żadnego znaczenia. W szczególności, żadnej różnicy nie powinniśmy odczuć, zamieniwszy miejscami pętle w programie. Program nadal wykona takie same obliczenia, taką samą liczbę razy, tylko w innej kolejności.

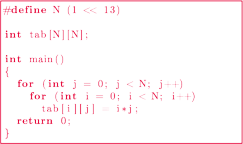
Program 1 Tabliczka mnożenia

Jednak okazuje się, że kolejność pętli w programie ma znaczenie. Na komputerze średniej klasy program 1 wykonywał się przez 7,93 s. Z kolei po zamianie pętli miejscami przyspieszył do 1,32 s. Zysk ponad sześciokrotny!

Drugi przykład. Mamy program 2, który w pętli oblicza sumy dwudziestu elementów tablicy. Zastanówmy się, co się stanie, gdy linijkę, w której deklarujemy tablicę tab, zamienimy na  int tab[N][M+512];? Teoretycznie nie powinno to spowodować żadnych zmian – program wciąż wykona taką samą liczbę instrukcji. Wprawdzie zadeklarowaliśmy trochę więcej pamięci, jednak procesor na tę dodatkową pamięć nawet nie spojrzy. Czy aby na pewno?

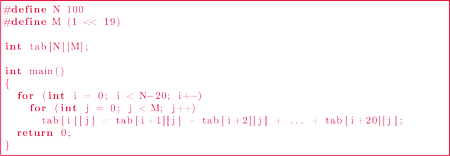
Program 2 Sumowanie tablicy

Ponownie przyjrzyjmy się czasom działania obu wersji programu. W pierwszej wersji program działa 13,16 s, a po powiększeniu tablicy – o blisko 10 sekund szybciej, tj. 3,18 s.

Skąd wynikają te anomalie czasowe? Z powodu abstrakcji! Podczas omawiania powyższych programów nie zastanawialiśmy się w ogóle, jak procesor interpretuje poszczególne instrukcje i co jest dla niego „wygodniejsze”. Skupiliśmy się jedynie na tym, że w obu programach wykonywane są takie same instrukcje, i to tyle samo razy. Przyjrzymy się teraz budowie i działaniu pamięci cache, aby lepiej zrozumieć, czym różnią się omawiane przez nas przykłady.

W przeciętnym komputerze możemy wyróżnić kilka rodzajów pamięci. Mamy dyski twarde, pamięć RAM oraz pamięć podręczną procesora (tzw. pamięć cache). Te typy pamięci różnią się rozmiarem, ceną oraz czasem dostępu. Dyski twarde są ogromne; za jeden gigabajt płacimy parę złotych, a czas dostępu jest rzędu 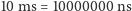(nanosekund). Pamięć RAM jest już dużo mniejsza niż dyski twarde; za jeden GB zapłacimy kilkadziesiąt złotych, a czas dostępu do pamięci jest rzędu 60 ns. Pamięć cache procesora jest malutka; za jeden gigabajt tego rodzaju pamięci zapłacimy kilkanaście tysięcy złotych. Za to czas dostępu do tego rodzaju pamięci jest rzędu kilku nanosekund.

Dążeniem twórców sprzętu jest taki model komputera, w którym średnia cena za gigabajt pamięci w całym komputerze byłaby zbliżona do ceny gigabajtu dysku twardego, natomiast średni czas dostępu do pamięci byłby rzędu czasu dostępu do pamięci cache. Cel ten, jak łatwo się domyślić, jest – póki co – niemożliwy do uzyskania, jednak nasze komputery są bliżej tego modelu, niż mogłoby nam się wydawać.

W cache’u nie możemy zmieścić pamięci całego programu. Pojawia się pewien problem – gdy procesor potrzebuje użyć jakiejś zmiennej, to powinna się ona już znajdować w pamięci cache. Zatem maszyna musi zabawić się w jasnowidza i spróbować przewidzieć, jakie zmienne będą przez program użyte w najbliższej przyszłości. Na szczęście komputerowi z pomocą przychodzi zasada lokalności. Mówi ona, że jeśli jakiś adres pamięci jest właśnie używany, to prawdopodobnie za chwilę będzie znowu potrzebny – albo on, albo adresy znajdujące się blisko niego. Przykładami mogą być listy rozkazów (po wykonaniu rozkazu prawdopodobnie będzie wykonywany rozkaz znajdujący się bezpośrednio po nim) albo tablice (jeśli jakiś element został wykorzystany, to za chwilę prawdopodobnie będziemy potrzebować sąsiedniego elementu).

Ogólna zasada działania pamięci cache jest następująca. Procesor prosi o jakiś adres pamięci. Pamięć cache sprawdza, czy taki adres zawiera. Jeśli tak, to przesyła go do procesora. Jeśli nie, to ściąga go z pamięci RAM wraz z całym blokiem (pamięć RAM jest podzielona na mniejsze porcje informacji, zwane blokami), a następnie przesyła procesorowi potrzebne dane.

Opiszemy teraz, jak bloki umieszczane są w pamięci cache. Zazwyczaj używane jest jedno z tzw. mapowań: skojarzeniowe, sekcyjne i sekcyjno-skojarzeniowe, przy czym w praktyce najczęściej ostatnie. My jednak skupimy się na mapowaniu sekcyjnym, gdyż jest do niego bardzo podobne, a zarazem nieco łatwiejsze do opisania.

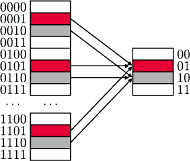
Rys. 1

Pamięć cache jest podzielona na sekcje – są to odpowiedniki bloków w pamięci RAM. Każdemu blokowi RAM-u przyporządkowana jest jedna sekcja w pamięci cache, wyznaczona przez jego adres modulo liczba sekcji (Rys. 1), która to liczba jest zawsze potęgą dwójki. Dzięki temu, aby „obliczyć”, jaki adres sekcji przyporządkowaliśmy danemu blokowi, nie potrzebujemy wykonywać żadnych pracochłonnych operacji – wystarczy spojrzeć na ostatnie bity adresu bloku. Ponadto, operacja modulo gwarantuje nam, że kilka sąsiednich bloków pamięci RAM może się w tym samym czasie znajdować w pamięci cache (co jest korzystne ze względu na zasadę lokalności). Z drugiej strony może się, oczywiście, zdarzyć, że kilku blokom jest przyporządkowana ta sama sekcja – wówczas w momencie sprowadzania kolejnego z tych bloków do cache’u, poprzedni zostanie nadpisany.

Po tej nieco dokładniejszej analizie mechanizmu działania pamięci podręcznej procesora przyjrzyjmy się ponownie naszym programom. W pierwszym z nich istotną rolę niespodziewanie odgrywała kolejność pętli. Aby zrozumieć, skąd wzięła się tak duża różnica, musimy sprawdzić, w jakiej kolejności w pamięci ułożone są kolejne elementy tablicy dwuwymiarowej. Nietrudno sprawdzić (na przykład pisząc prosty program w języku C/C++), że tablica taka zajmuje spójny obszar pamięci. Ułożona jest w następujący sposób: 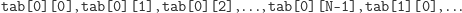 itd. W takiej kolejności przeglądamy tablicę, jeżeli odwrócimy kolejność pętli w programie 1. Dzięki temu działa zasada lokalności i procesor łatwo przewiduje, które adresy pamięci będą za chwilę potrzebne. W oryginalnym programie 1 przeglądamy tablicę w sposób dla procesora bardzo chaotyczny. Komórka tab[0][0] w ogóle nie leży w pobliżu tab[1][0], przez co procesor, próbując przewidzieć, jakie kolejne adresy będą wykorzystywane, nieustannie się myli, więc musi przesyłać z pamięci RAM do pamięci cache ciągle nowe adresy – a to ma negatywny wpływ na czas działania programu.

Drugi program wydaje się jeszcze ciekawszy. Faktycznie, w pierwszym programie w celu usprawnienia zmieniliśmy kolejność wykonywania instrukcji, natomiast w tym przypadku nawet tego nie zrobiliśmy! Sekret tkwi w tym, że w pierwszej wersji programu 2 drugi wymiar tablicy był potęgą dwójki (choć tak naprawdę ważne jest tylko to, że był on wielokrotnością rozmiaru pamięci cache mojego procesora) – patrz rysunek 2. Dlatego komórki 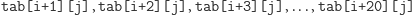 trafiały zawsze do tej samej sekcji w pamięci podręcznej. Przebieg tego programu wyglądał więc następująco. Aby obliczyć tab[i][j], procesor musi dodać komórki 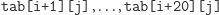 – prosi więc pamięć cache najpierw o  tab[i+1][j]. Pamięć cache jej nie ma, więc ściąga z pamięci RAM. Następnie procesor prosi o  tab[i+2][j]. Pamięć cache jej nie ma (w sekcji, w której powinna być ta komórka, jest tab[i+1][j]), więc pobiera ją z pamięci głównej, i tak dalej aż do  tab[i+20][j]. Następnie procesor musi obliczyć tab[i][j+1], co znowu wymagać będzie dwudziestu ściągnięć bloku do pamięci cache itd.

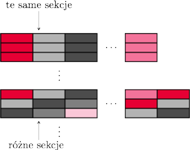
Rys. 2

Gdy zwiększymy liczbę kolumn w tablicy o długość bloku, zagwarantujemy, że komórki 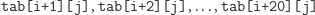 będą trafiać do sąsiednich sekcji w pamięci podręcznej.

I choć przy obliczaniu pierwszej sumy będzie trzeba wszystkie te bloki ściągnąć do pamięci cache, to przy obliczaniu sumy 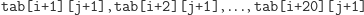 odpowiednie bloki będą się już znajdować w pamięci podręcznej, dzięki czemu program nie straci cennych nanosekund.

Być może ktoś powie, że nie warto się w to wszystko w ogóle zagłębiać, gdyż przyspieszamy program jedynie o stały czynnik. Jednak nakład pracy, jaki włożyliśmy w zmianę programów, był minimalny. Jeśli mamy program działający 10 godzin, a potrzebujemy otrzymać wynik w ciągu godziny, to owszem – możemy kupić dziesięciokrotnie szybszy komputer. Ale czasami możemy zaoszczędzić dużo pieniędzy, po prostu zamieniając kilka linijek miejscami i dodając kilka pozornie nieistotnych znaków w odpowiednich miejscach programu.

Na koniec małe ćwiczenie dla Ciebie, Drogi Czytelniku. Otwórz swoją ulubioną wyszukiwarkę internetową i wyszukaj „mnożenie macierzy C++”. Wejdź na pierwszą lepszą stronę. Czy implementacja, którą znalazłeś, jest napisana optymalnie z punktu widzenia działania mechanizmu cache? Czy można ją przyspieszyć, używając metod opisanych w tym artykule? Jak to zrobić?