Informatyczny kącik olimpijski
Neon
O pewnym zadaniu z zeszłorocznego Obozu Naukowo-Treningowego im. A. Kreczmara.
Na przykład dla neonu supermarket stokrotka możemy uzyskać 17 różnych niepustych podciągów (skt, sra, srk, srt i ich krótsze podciągi) na 27 sposobów (np. srk możemy uzyskać na 2 sposoby). Wynik należy obliczyć modulo pewna liczba całkowita.
Zadanie rozwiążemy, używając metody programowania dynamicznego. Niech
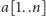 i
i
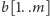 będą słowami neonu. Będziemy wypełniać prostokątną
tablicę
będą słowami neonu. Będziemy wypełniać prostokątną
tablicę
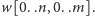 Dla
Dla
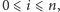
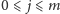 oznaczmy
przez
oznaczmy
przez
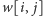 liczbę sposobów, na jakie możemy zgasić litery
w słowach
liczbę sposobów, na jakie możemy zgasić litery
w słowach
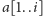 oraz
oraz
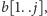 tak by pozostałe litery tworzyły ten
sam (być może pusty) podciąg. Odpowiedzią do pierwszej części zadania jest,
oczywiście,
tak by pozostałe litery tworzyły ten
sam (być może pusty) podciąg. Odpowiedzią do pierwszej części zadania jest,
oczywiście,
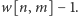
Jeśli
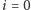 lub
lub
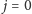 (tzn. gdy jedno ze słów jest puste), to
możemy utworzyć tylko pusty podciąg, zatem
(tzn. gdy jedno ze słów jest puste), to
możemy utworzyć tylko pusty podciąg, zatem
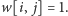
Załóżmy zatem, że
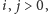 i spójrzmy na ostatnie litery słów
i spójrzmy na ostatnie litery słów
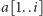 i
i
 Załóżmy na początek, że są one równe, tzn.
Załóżmy na początek, że są one równe, tzn.
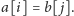 Rozważmy cztery przypadki w zależności od
tego, czy zostawiamy te litery zapalone, czy też nie. Jeśli obie będą
zapalone, to znaczy, że uzyskane podciągi powstają z rozszerzenia jednego
z podciągów dla słów
Rozważmy cztery przypadki w zależności od
tego, czy zostawiamy te litery zapalone, czy też nie. Jeśli obie będą
zapalone, to znaczy, że uzyskane podciągi powstają z rozszerzenia jednego
z podciągów dla słów
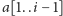 i
i
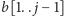 o dodatkową
literę. To daje
o dodatkową
literę. To daje
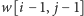 możliwości. Liczba możliwych
podciągów w przypadku, gdy litera
możliwości. Liczba możliwych
podciągów w przypadku, gdy litera
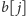 zostanie zgaszona, wynosi
zostanie zgaszona, wynosi
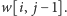 Analogicznie liczba podciągów, gdy litera
Analogicznie liczba podciągów, gdy litera
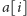 zostanie
zgaszona, wynosi
zostanie
zgaszona, wynosi
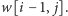 Zauważmy, że te podciągi, które wystąpią
w przypadku zgaszenia obu tych liter, uwzględniliśmy już w wyniku, z tym
że policzyliśmy je dwukrotnie, należy zatem odjąć ich liczbę (jest
ich
Zauważmy, że te podciągi, które wystąpią
w przypadku zgaszenia obu tych liter, uwzględniliśmy już w wyniku, z tym
że policzyliśmy je dwukrotnie, należy zatem odjąć ich liczbę (jest
ich
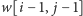 ). Ostatecznie dostajemy prostą zależność
). Ostatecznie dostajemy prostą zależność
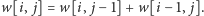
Przypadek
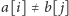 jest trochę łatwiejszy: nie możemy naraz zapalić liter
jest trochę łatwiejszy: nie możemy naraz zapalić liter
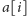 i
i
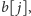 zatem
zatem
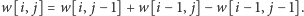 Zajmiemy
się teraz drugą częścią zadania: obliczeniem liczby różnych wspólnych
podciągów. Na pierwszy rzut oka może się wydawać, że w tym przypadku
będziemy musieli zastosować zupełnie inną strategię i potrzebna będzie jakaś
struktura danych, która umożliwi nam wyłapywanie duplikatów. Okazuje się
jednak, że i ten problem można rozwiązać za pomocą zaskakująco prostej
zależności rekurencyjnej.
Zajmiemy
się teraz drugą częścią zadania: obliczeniem liczby różnych wspólnych
podciągów. Na pierwszy rzut oka może się wydawać, że w tym przypadku
będziemy musieli zastosować zupełnie inną strategię i potrzebna będzie jakaś
struktura danych, która umożliwi nam wyłapywanie duplikatów. Okazuje się
jednak, że i ten problem można rozwiązać za pomocą zaskakująco prostej
zależności rekurencyjnej.
Niech
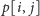 oznacza liczbę różnych wspólnych podciągów, które
możemy utworzyć w słowach
oznacza liczbę różnych wspólnych podciągów, które
możemy utworzyć w słowach
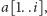
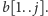 Dla
Dla
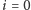 lub
lub
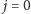 mamy, oczywiście,
mamy, oczywiście,
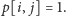 Znów patrzymy na ostatnie
litery słów. Niech
Znów patrzymy na ostatnie
litery słów. Niech
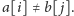 Okazuje się, że w tym przypadku mamy
po prostu
Okazuje się, że w tym przypadku mamy
po prostu
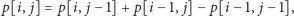 a rozumowanie
jest analogiczne jak dla tablicy
a rozumowanie
jest analogiczne jak dla tablicy
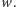
Niech teraz
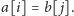 Każdy wspólny podciąg słów
Każdy wspólny podciąg słów
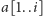 i
i
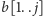 należy do co najmniej jednego z dwóch
zbiorów: zbioru
należy do co najmniej jednego z dwóch
zbiorów: zbioru
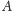 tych różnych podciągów, które mogą
powstać, gdy obie litery
tych różnych podciągów, które mogą
powstać, gdy obie litery
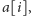
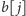 są zapalone, oraz zbioru
są zapalone, oraz zbioru
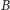 tych różnych podciągów, które mogą powstać, gdy obie
te litery są zgaszone. Zatem
tych różnych podciągów, które mogą powstać, gdy obie
te litery są zgaszone. Zatem
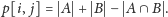 Zbiory
Zbiory
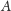 i
i
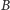 mają po
mają po
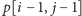 elementów, pozostaje
zatem obliczyć liczność ich części wspólnej
elementów, pozostaje
zatem obliczyć liczność ich części wspólnej
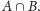 Niech
Niech
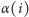 oznacza największą liczbę dodatnią mniejszą niż
oznacza największą liczbę dodatnią mniejszą niż
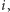 dla
której
dla
której
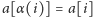 ; analogicznie niech
; analogicznie niech
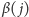 będzie największą
liczbą
będzie największą
liczbą
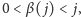 dla której
dla której
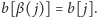 Jeśli choć
jedna z tych liczb nie istnieje, to
Jeśli choć
jedna z tych liczb nie istnieje, to
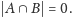 W przeciwnym
przypadku mamy
W przeciwnym
przypadku mamy
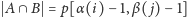 i wówczas
i wówczas
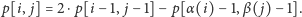
Pozostaje oszacować złożoność naszego algorytmu. Tablice
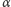 i
i
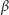 możemy obliczyć w czasie
możemy obliczyć w czasie
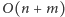 i takiej pamięci. Czas
wypełniania tablic
i takiej pamięci. Czas
wypełniania tablic
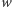 i
i
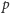 to
to
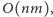 bezpośrednia
realizacja da też taką złożoność pamięciową. Zauważmy jednak, że
w przypadku tablicy
bezpośrednia
realizacja da też taką złożoność pamięciową. Zauważmy jednak, że
w przypadku tablicy
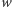 możemy zastosować standardową sztuczkę:
jeśli wypełniamy tablicę wierszami, wystarczy trzymać w pamięci jedynie
aktualny (
możemy zastosować standardową sztuczkę:
jeśli wypełniamy tablicę wierszami, wystarczy trzymać w pamięci jedynie
aktualny (
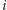 -ty) i ostatnio wypełniony (
-ty) i ostatnio wypełniony (
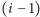 -szy) wiersz – nigdy
bowiem nie odwołujemy się do komórek z wierszy o numerach mniejszych
niż
-szy) wiersz – nigdy
bowiem nie odwołujemy się do komórek z wierszy o numerach mniejszych
niż
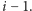 Problem powstaje w przypadku tablicy
Problem powstaje w przypadku tablicy
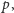 w której
korzystamy z wiersza o numerze
w której
korzystamy z wiersza o numerze
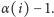 Tu jednak radzimy sobie
następująco: oprócz ostatnich dwóch wierszy trzymamy dodatkowo tablicę
Tu jednak radzimy sobie
następująco: oprócz ostatnich dwóch wierszy trzymamy dodatkowo tablicę
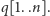 W przypadku, gdy
W przypadku, gdy
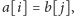 uaktualniamy
ją według wzoru
uaktualniamy
ją według wzoru
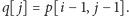 Dzięki temu mamy
Dzięki temu mamy
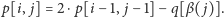 Ostatecznie złożoność
pamięciowa algorytmu wyniesie
Ostatecznie złożoność
pamięciowa algorytmu wyniesie