Informatyczny kącik olimpijski
Samogenerujący się ciąg
W tym numerze Delty dużo uwagi poświęcono ciągowi EKG, który
zarówno z matematycznego, jak i z informatycznego punktu widzenia
przejawia wiele interesujących własności. W kąciku kontynuujemy temat
ciekawych ciągów liczbowych. Zajmiemy się zadaniem Ciąg z finału
II Olimpiady Informatycznej Gimnazjalistów, w którym poproszono
uczestników o wyznaczenie
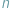 -tego wyrazu pewnego ciągu, zwyczajowo
wiązanego z nazwiskiem matematyka Solomona Golomba.
-tego wyrazu pewnego ciągu, zwyczajowo
wiązanego z nazwiskiem matematyka Solomona Golomba.
Ciąg ten jest niemalejącą sekwencją liczb całkowitych dodatnich
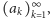 taką
że
taką
że
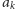 oznacza łączną liczbę wystąpień liczby
oznacza łączną liczbę wystąpień liczby
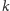 w tej sekwencji.
To już cała definicja; spróbujmy rozszyfrować, jak wygląda ten tajemniczy
ciąg.
w tej sekwencji.
To już cała definicja; spróbujmy rozszyfrować, jak wygląda ten tajemniczy
ciąg.
Zacznijmy od początku, czyli od wyrazu
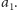 Ponieważ
Ponieważ
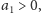 więc w ciągu musi wystąpić co najmniej jedna jedynka,
a skoro ciąg jest niemalejący, to musi zaczynać się od jedynki, czyli
więc w ciągu musi wystąpić co najmniej jedna jedynka,
a skoro ciąg jest niemalejący, to musi zaczynać się od jedynki, czyli
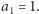 Przejdźmy teraz do
Przejdźmy teraz do
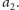 Otóż nie może być
Otóż nie może być
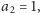 gdyż w ciągu mamy dokładnie jedną jedynkę (
gdyż w ciągu mamy dokładnie jedną jedynkę (
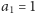 ). Stąd
). Stąd
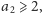 czyli – podobnie jak poprzednio – w ciągu jest co najmniej jedna
dwójka, więc
czyli – podobnie jak poprzednio – w ciągu jest co najmniej jedna
dwójka, więc
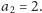 To oznacza, że w ciągu mamy łącznie
dwie dwójki, czyli
To oznacza, że w ciągu mamy łącznie
dwie dwójki, czyli
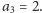 A zatem w ciągu mamy dwie trójki,
A zatem w ciągu mamy dwie trójki,
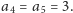 To z kolei oznacza, że mamy po trzy czwórki i piątki, czyli
nasz ciąg zaczyna się tak: 1, 2, 2, 3, 3, 4, 4, 4, 5, 5, 5.
To z kolei oznacza, że mamy po trzy czwórki i piątki, czyli
nasz ciąg zaczyna się tak: 1, 2, 2, 3, 3, 4, 4, 4, 5, 5, 5.
Widzimy, że możemy dalej rozumować w ten sposób; co więcej,
otrzymujemy algorytm na generowanie wyrazów ciągu Golomba. Startujemy
od
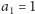 i
i
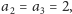 po czym dla każdego kolejnego
po czym dla każdego kolejnego
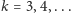 na koniec ciągu wstawiamy
na koniec ciągu wstawiamy
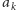 wyrazów równych
wyrazów równych
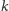 (ciąg reprezentujemy w zwykłej tablicy). Za każdym razem dodajemy
więcej niż jeden wyraz, więc nigdy nie będziemy musieli „zgadywać” – kiedy
dojdziemy do indeksu
(ciąg reprezentujemy w zwykłej tablicy). Za każdym razem dodajemy
więcej niż jeden wyraz, więc nigdy nie będziemy musieli „zgadywać” – kiedy
dojdziemy do indeksu
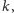 będziemy już znali
będziemy już znali
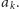 Kontynuujemy to
postępowanie, aż przypiszemy wartość
Kontynuujemy to
postępowanie, aż przypiszemy wartość
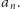 Koszt czasowy i, niestety,
także pamięciowy to
Koszt czasowy i, niestety,
także pamięciowy to
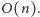 Za taki naturalny algorytm można było na
zawodach uzyskać 40% punktów.
Za taki naturalny algorytm można było na
zawodach uzyskać 40% punktów.
Spróbujmy usprawnić ten algorytm, przede wszystkim pod względem
zapotrzebowania na pamięć. Kluczowe spostrzeżenie już właściwie
poczyniliśmy poprzednio: kiedy natrafiamy na wyraz
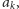 dopisujemy
na koniec ciągu pełne
dopisujemy
na koniec ciągu pełne
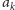 nowych wyrazów, a tymczasem przesuwamy
się indeksem zaledwie o 1 (do
nowych wyrazów, a tymczasem przesuwamy
się indeksem zaledwie o 1 (do
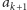 ). A im dalej, tym
). A im dalej, tym
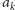 jest
większe. To oznacza, że istotnie rośnie nam „ogon” już obliczonych
wartości, które pozostają do przejrzenia. Algorytm może się zakończyć, gdy
już przetworzony fragment ciągu wraz z tym ogonem ma co najmniej
jest
większe. To oznacza, że istotnie rośnie nam „ogon” już obliczonych
wartości, które pozostają do przejrzenia. Algorytm może się zakończyć, gdy
już przetworzony fragment ciągu wraz z tym ogonem ma co najmniej
 wyrazów. Ponieważ ogon jest długi, więc będziemy przechowywać
w tablicy tylko pewną początkową liczbę wyrazów ciągu, a ponadto będziemy
pamiętać długość pozostałego ogona.
wyrazów. Ponieważ ogon jest długi, więc będziemy przechowywać
w tablicy tylko pewną początkową liczbę wyrazów ciągu, a ponadto będziemy
pamiętać długość pozostałego ogona.
Oznaczmy przez
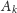 sumę
sumę
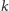 początkowych wyrazów ciągu
początkowych wyrazów ciągu
 (niech
(niech
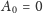 ). W tablicy musimy przechowywać jedynie
pierwsze
). W tablicy musimy przechowywać jedynie
pierwsze
 wyrazów ciągu, takich że
wyrazów ciągu, takich że
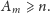 Jak duże musi
być to
Jak duże musi
być to
 ? Sprawdźmy eksperymentalnie! Za pomocą poprzedniego
algorytmu obliczamy, że
? Sprawdźmy eksperymentalnie! Za pomocą poprzedniego
algorytmu obliczamy, że
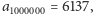 co pozwala zgadnąć, iż
co pozwala zgadnąć, iż
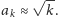 Przy tym założeniu mamy, że
Przy tym założeniu mamy, że

Stąd
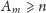 dla
dla
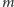 rzędu
rzędu
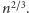 Jest to istotnie lepiej niż
poprzednio, a sam algorytm pozostał prosty: obliczamy początkowy fragment
ciągu długości rzędu
Jest to istotnie lepiej niż
poprzednio, a sam algorytm pozostał prosty: obliczamy początkowy fragment
ciągu długości rzędu
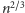 (dokładną długość możemy wyznaczyć
eksperymentalnie, rozważając górne ograniczenie na
(dokładną długość możemy wyznaczyć
eksperymentalnie, rozważając górne ograniczenie na
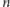 ), po czym
obliczamy kolejne
), po czym
obliczamy kolejne
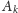 do momentu, gdy
do momentu, gdy
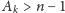 ; wówczas
; wówczas
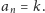 Za takie podejście można było otrzymać 70% punktów;
pozwala ono obliczyć np.
Za takie podejście można było otrzymać 70% punktów;
pozwala ono obliczyć np.
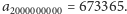 To oznacza, że musi
dać się jeszcze lepiej! W poprzedniej metodzie z
To oznacza, że musi
dać się jeszcze lepiej! W poprzedniej metodzie z
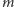 -elementowego
początkowego fragmentu ciągu wnioskowaliśmy o
-elementowego
początkowego fragmentu ciągu wnioskowaliśmy o
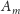 wyrazach ciągu.
Teraz zwiększymy tę liczbę.
wyrazach ciągu.
Teraz zwiększymy tę liczbę.
Załóżmy, że mamy obliczone
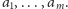 Wówczas dla każdego
Wówczas dla każdego
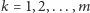 wiemy, że na pozycjach
wiemy, że na pozycjach
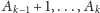 w naszym
ciągu pojawia się liczba
w naszym
ciągu pojawia się liczba
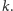 To z kolei oznacza, iż każda z
To z kolei oznacza, iż każda z
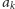 liczb
liczb
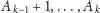 występuje w ciągu
występuje w ciągu
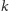 razy. Nasz ciąg wygląda
zatem tak: jedno wystąpienie liczby
razy. Nasz ciąg wygląda
zatem tak: jedno wystąpienie liczby
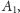 po dwa wystąpienia liczb
po dwa wystąpienia liczb
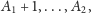 po trzy wystąpienia liczb
po trzy wystąpienia liczb
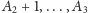 itd. W ten
sposób na podstawie pierwszych
itd. W ten
sposób na podstawie pierwszych
 wyrazów ciągu jesteśmy w stanie
ustalić
wyrazów ciągu jesteśmy w stanie
ustalić
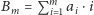 początkowych wyrazów ciągu. Liczbę
początkowych wyrazów ciągu. Liczbę
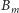 szacujemy podobnie jak poprzednio:
szacujemy podobnie jak poprzednio:

Stąd warunek
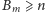 zachodzi już dla
zachodzi już dla
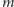 rzędu
rzędu
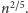 Dokładny
opis algorytmu opartego na wartościach
Dokładny
opis algorytmu opartego na wartościach
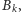 podobny do poprzedniego,
pozostawiamy Czytelnikowi. To jest rozwiązanie wzorcowe tego zadania; za
jego pomocą obliczamy, że np.
podobny do poprzedniego,
pozostawiamy Czytelnikowi. To jest rozwiązanie wzorcowe tego zadania; za
jego pomocą obliczamy, że np.
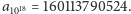 Na koniec
winni jesteśmy Czytelnikowi drobne sprostowanie: otóż odgadnięte
oszacowanie
Na koniec
winni jesteśmy Czytelnikowi drobne sprostowanie: otóż odgadnięte
oszacowanie
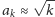 jest nieprawdziwe, lecz nie jest zbyt odległe
od poprawnego. W rzeczywistości
jest nieprawdziwe, lecz nie jest zbyt odległe
od poprawnego. W rzeczywistości
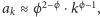 przy czym
przy czym
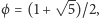 czyli
czyli
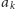 jest rzędu
jest rzędu
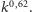 Po więcej
informacji na ten temat odsyłamy do Internetowej Encyklopedii Ciągów
Liczbowych, którą, swoją drogą, polecamy wszystkim miłośnikom ciekawych
ciągów.
Po więcej
informacji na ten temat odsyłamy do Internetowej Encyklopedii Ciągów
Liczbowych, którą, swoją drogą, polecamy wszystkim miłośnikom ciekawych
ciągów.
I jeszcze pytanie do Czytelnika: czy można dalej usprawniać podane
algorytmy, wprowadzając odpowiednie ciągi pomocnicze
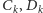 itd.?
itd.?