Dzisiaj Bajtazar zamierza tresować swoje ulubione 10 pcheł, którym swego czasu nadał pieszczotliwe imiona będące kolejnymi literami alfabetu łacińskiego. Wiemy, że Bajtazar napisał na żetonach następujące liczby:

oraz że ustawił swoje pchły w kolejności alfabetycznej. A zatem na początku tańca pchły tworzą układ

oznaczany w skrócie ABCDEFGHIJ, po pierwszym takcie muzyki – układ:

oznaczany w skrócie FDJBHGACIE, po drugim takcie muzyki – układ GBEDCAFJIH itd. Bajtazar zastanawia się, jaki będzie układ pcheł po odtańczeniu całej piątej symfonii Bajthovena, która dziwnym trafem składa się z dokładnie 2011 taktów.

Spróbujmy pomóc Bajtazarowi przewidzieć ten układ. Zacznijmy od przyjrzenia się, jakie są kolejne pozycje zajmowane przez jedną, ustaloną pchłę Bajtazara, powiedzmy pchłę A. Swój taniec zaczyna ona na żetonie 1, po pierwszym skoku znajduje się na żetonie 7, dalej na żetonie 6, po trzech skokach ląduje z powrotem na żetonie 1…Widać, że dalej pozycje pchły A będą się cyklicznie powtarzać, przy czym po skoku o numerze podzielnym przez 3 będzie to żeton 1, jeśli numer skoku daje resztę 1 z dzielenia przez 3, to żeton 7, a po wszystkich pozostałych skokach żeton 6. Ponieważ 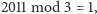więc po odtańczeniu symfonii pchła będzie odpoczywać na żetonie 7.

Po tym samym cyklu 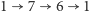skaczą także pchły F i G; łatwo sprawdzamy, że po 2011. skoku znajdują się one odpowiednio na żetonach 1 i 6. Znamy już zatem część wynikowego układu: F????GA???.

Widzimy dalej, że pchła I skacze w miejscu, mamy zatem: F????GA?I?. Coś takiego należało w sumie zauważyć wcześniej.

Dalej, pchła B: startuje z żetonu 2, po pierwszym skoku ląduje na żetonie 4, po drugim znów na żetonie 2. Mamy cykl 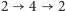z pchłami B i D, a ponieważ 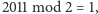więc możemy uzupełnić nasz układ: FD?B?GA?I?.

Pchła C: zaczyna na żetonie 3, przeskakuje na żeton 8, potem na żeton 5, potem na żeton 10, wreszcie po czwartym skoku ląduje z powrotem na żetonie 3. Mamy cykl 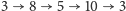z pchłami C, H, E, J. Ponieważ 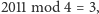więc na końcu symfonii pchła C znajdzie się na żetonie 10, pchła H na żetonie 3, pchła E na żetonie 8, a pchła J na żetonie 5. Ostateczny układ po 2011 skokach to FDHBJGAEIC.

Bajtazar bardzo się ucieszył, że pomogliśmy mu obliczyć końcowy układ taneczny, gdyż dzięki temu nie będzie musiał wysłuchiwać całej symfonii, żeby go poznać. Teraz zastanawia się, ile różnych układów swoich pcheł zobaczyłby do końca symfonii.

Dotychczasowa analiza tańca pcheł pozwala dostrzec okresowość zmian ich położeń: mamy mianowicie cykle długości 1, 2, 3 i 4. Jeśli pchły wykonają 12 skoków, która to liczba jest najmniejszą wspólną wielokrotnością (w skrócie NWW) długości wszystkich cykli, to pchły w ramach każdego cyklu wrócą do początkowego układu, czyli otrzymamy układ ABCDEFGHIJ. Z naszego rozkładu na cykle widać, że ten początkowy układ nie powtórzy się wcześniej, a z tego faktu można wywnioskować, że żaden inny układ nie powtórzy się podczas pierwszych 12 taktów muzyki. Czyli mamy dokładnie 12 różnych układów, które w dalszych skokach będą powtarzały się w kółko.

Była to dla Bajtazara fatalna wiadomość – zaplanowany przez niego taniec okazał się strasznie monotonny! W akcie desperacji poprosił nas o jeszcze jedną przysługę: chce, żebyśmy sprawdzili, czy nie da się jakoś inaczej napisać liczb na żetonach, żeby podczas tańca wystąpiło więcej różnych układów? Bajtazar gdzieś usłyszał, że wszystkich permutacji liter wyrazu ABCDEFGHIJ jest 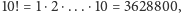i zastanawia się, na ile możemy zbliżyć się do tej liczby.

I tym razem wesprzemy Bajtazara i spróbujemy wskazać najlepszą konfigurację liczb na żetonach. Ograniczmy najpierw liczbę możliwości, jakie musimy rozważyć. Przede wszystkim zauważmy, że odkryte przez nas dotychczas własności związane z rozkładem na cykle zachodzą dla dowolnej konfiguracji. Po pierwsze, pchła startująca z danego żetonu musi w końcu na ten żeton wrócić – mówiąc obrazowo, trasa każdej pchły jest cyklem (litera „O”), a nie cyklem z odnóżką (litera „P”), gdyż w przeciwnym przypadku jedna z liczb zapisanych na żetonach musiałaby się powtórzyć (ta na styku pałki i dolnej części brzuszka w literze „P”). Po drugie, liczbę różnych układów podczas tańca możemy obliczyć jako najmniejszą wspólną wielokrotność długości cykli poszczególnych pcheł. To oznacza, że rozwiązaniem zagadki Bajtazara jest taki podział liczby 10 na całkowite dodatnie składniki, w którym NWW jest największe.

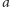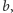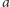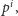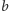Niestety, takich podziałów liczby 10 wciąż może być dużo. Spróbujmy znów zredukować liczbę możliwości. Intuicja podpowiada, że nie opłaca się wybierać dwóch składników, które mają jakiś wspólny dzielnik większy niż 1. Istotnie, jeśli mamy składniki oraz przy czym w rozkładzie na czynniki pierwsze zawiera czynnik a czynnik 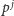oraz 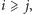to możemy bez straty dla NWW zastąpić 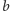mniejszym składnikiem 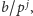a powstałe w ten sposób niezagospodarowane żetony ustawić chociażby w cykle jednoelementowe.

Dalej, możemy ograniczyć zbiór rozważanych składników. I tak, zamiast brać do podziału składnik 6, możemy równie dobrze wziąć składniki 2 i 3 – NWW nie zmieni się, a zyskamy jeden wolny żeton do zagospodarowania. Podobnie, nie opłaca się rozważać składnika 10 i, ogólniej, żadnego składnika niebędącego potęgą liczby pierwszej. Akurat wśród liczb z zakresu 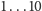wszystkie pozostałe są już potęgami liczb pierwszych.

Udało nam się już ograniczyć rozważania do podziałów liczby 10 na parami względnie pierwsze składniki, wśród których nie występują liczby 6 oraz 10. Tego już nie ma tak dużo; rozpatrzmy wszystkie możliwości, poczynając od największych możliwych składników. Przypomnijmy, że konfiguracja Bajtazara dała nam NWW równe 12, więc mniejszych NWW na pewno nie musimy rozważać.

W podziale zawierającym 9 lub 8 mogą występować już tylko same jedynki – w ten sposób nie pobijemy konfiguracji Bajtazara. Jeśli weźmiemy 7, to możemy do tego dołożyć zestaw składników (3), (2, 1) lub (1, 1, 1), z których ten pierwszy jest najlepszy i daje NWW równe 21. Świetnie, już mamy konfigurację lepszą od konfiguracji Bajtazara. Szóstki nie rozważamy, to teraz piątka. Do piątki możemy dołożyć (4, 1), (3, 2), (3, 1, 1) oraz pewne zestawy liczb nieprzekraczających 2, które na pewno się nam nie opłacają. Z wcześniejszych możliwości najlepsza jest środkowa, daje już NWW równe 30. Dalej jest już tylko gorzej: do czwórki nie jesteśmy w stanie dołożyć niczego, co pozwoliłoby przekroczyć NWW 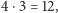a z trójką, dwójką i jedynką jest zdecydowanie nie lepiej.

No to koniec: rozważyliśmy wszystkie możliwości i możemy z dumą odpowiedzieć Bajtazarowi, że nie da się znaleźć konfiguracji liczb na żetonach, przy której pchły zaliczą więcej niż 30 różnych układów. A taką właśnie liczbę układów daje, przykładowo, konfiguracja: 2, 3, 4, 5, 1, 7, 8, 6, 10, 9, reprezentująca układ cykli (5, 3, 2).

No dobrze, a ile jest różnych konfiguracji liczb na żetonach dających właśnie 30 różnych układów tanecznych? A co jeśli pozwolimy na to, żeby liczby zapisane na żetonach mogły się powtarzać? A tak w ogóle, czy przy każdej konfiguracji mamy pewność, że pchły nie zderzą się w locie, co z pewnością spowodowałoby istną katastrofę podczas pokazu? Odpowiedzi na te i dalsze pytania rozochoconego Bajtazara pozostawiamy Drogiemu Czytelnikowi.