Informatyczny kącik olimpijski
Szukamy pola areału
Weźmy macierz
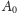 równą
równą

i zdefiniujmy rekurencyjnie ciąg macierzy, z których każda następna powstaje zgodnie ze wzorem:

Zatem
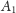 jest wymiaru
jest wymiaru
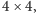
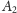 –
–
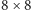 i tak dalej.
Kontynuując dostawianie macierzy, w ten sposób otrzymamy nieskończoną
macierz, którą oznaczamy
i tak dalej.
Kontynuując dostawianie macierzy, w ten sposób otrzymamy nieskończoną
macierz, którą oznaczamy
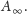
Zdefiniujmy areał jako spójny (w sensie sąsiedztwa wzdłuż boków, nie tylko
w wierzchołkach), maksymalny (tj. niedający się powiększyć) zbiór pól
macierzy o tych samych wartościach. W naszym zadaniu mamy dane
współrzędne pola w macierzy
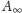 (wiersze i kolumny numerujemy od
(wiersze i kolumny numerujemy od
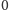 ). Należy obliczyć rozmiar areału zawierającego to pole (możliwe, że
jest on nieskończony).
). Należy obliczyć rozmiar areału zawierającego to pole (możliwe, że
jest on nieskończony).
Głównym problemem w tym zadaniu jest wyobraźnia – najpierw należy
wyobrazić sobie, jak właściwie wygląda macierz
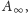 potem trzeba
wyobrażać sobie kształty i rozmiary areałów.
potem trzeba
wyobrażać sobie kształty i rozmiary areałów.
„Wycięty” z
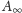 kwadrat o boku
kwadrat o boku
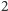 (zawierający pole
(zawierający pole
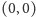 ) jest równy macierzy
) jest równy macierzy
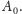 Jeśli kwadrat będzie miał bok
Jeśli kwadrat będzie miał bok
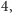 to będzie równy
to będzie równy
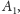 itd. Co więcej, wszystkie pola
itd. Co więcej, wszystkie pola
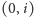 oraz
oraz
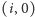 mają w
mają w
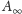 wartość
wartość
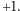
Jak więc wyglądają areały? Na pewno jest jeden areał nieskończony, zawierający
punkt
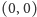 – choćby dlatego, że należą do niego wszystkie pola
– choćby dlatego, że należą do niego wszystkie pola
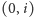 oraz
oraz
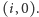 Weźmy teraz areał, do którego należy punkt
Weźmy teraz areał, do którego należy punkt
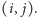 Niech
Niech
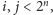 dla pewnego
dla pewnego
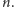 Wtedy pole
Wtedy pole
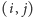 należy do
należy do
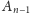 (ponieważ wymiar tej macierzy to
(ponieważ wymiar tej macierzy to
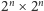 ).
Ale kiedy tworzymy
).
Ale kiedy tworzymy
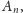 to na wszystkich polach
to na wszystkich polach
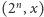 i
i
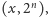 dla
dla
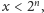 ląduje wartość
ląduje wartość
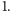 W takim razie albo
cały poszukiwany areał zawiera się w
W takim razie albo
cały poszukiwany areał zawiera się w
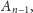 albo łączy z tym samym
areałem, do którego należy
albo łączy z tym samym
areałem, do którego należy
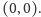 Jest więc tylko jeden areał
nieskończony.
Jest więc tylko jeden areał
nieskończony.

Macierz
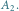 W obszarach obwiedzionych linią czarną znajdują się wartości
W obszarach obwiedzionych linią czarną znajdują się wartości
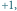 a kolorową
a kolorową
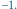 Zakreskowane areały są już zamknięte.
Zakreskowane areały są już zamknięte.
Mamy już pewien zbiór spostrzeżeń, spróbujmy więc podejść do
rozwiązania zadania. Definicja
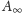 jest rekurencyjna – skorzystajmy więc
z tej samej techniki. Niech polem, którego areału poszukujemy, będzie pole
jest rekurencyjna – skorzystajmy więc
z tej samej techniki. Niech polem, którego areału poszukujemy, będzie pole
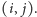 Na początek znajdźmy takie
Na początek znajdźmy takie
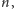 że
że
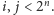 Nasze
obliczenia możemy zamknąć w macierzy
Nasze
obliczenia możemy zamknąć w macierzy
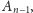 ponieważ (zgodnie
z poprzednimi stwierdzeniami) pole
ponieważ (zgodnie
z poprzednimi stwierdzeniami) pole
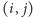 będzie albo należeć do
jedynego nieskończonego areału, albo jego areał będzie w całości zawarty
w
będzie albo należeć do
jedynego nieskończonego areału, albo jego areał będzie w całości zawarty
w
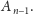
Na początek sprawdźmy, do której ćwiartki macierzy
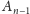 należy
należy
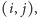 i dla tej ćwiartki wywołajmy poszukiwania rekurencyjnie (tj.
weźmy
i dla tej ćwiartki wywołajmy poszukiwania rekurencyjnie (tj.
weźmy
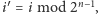
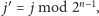
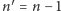 ).
).
Wyróżnijmy pewne rodzaje areałów, z którymi mamy do czynienia przy
obsłudze podmacierzy kwadratowej w
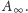 Niektóre z nich nie
stykają się z krawędziami tej macierzy – takie areały są „zamknięte”
i nie zostaną już powiększone. Pozostałe możemy podzielić na cztery
klasy:
Niektóre z nich nie
stykają się z krawędziami tej macierzy – takie areały są „zamknięte”
i nie zostaną już powiększone. Pozostałe możemy podzielić na cztery
klasy:
- A
- – areał zawierający lewy górny róg
- B
- – areał zawierający pole(a) na „dolnej” krawędzi macierzy
- C
- – areał zawierający pole(a) na „prawej” krawędzi macierzy
- D
- – areał spełniający B oraz C.
Wynikiem funkcji rekurencyjnej będzie wartość pola wraz z typem areału
w podmacierzy, do którego to pole należy. I to już nam wystarczy, bo z tych
danych możemy odtworzyć wartość pola i typ jego areału względem
dwukrotnie większej macierzy. Na przykład, jeśli wywołanie rekurencyjne dla
prawej-dolnej ćwiartki dało w wyniku wartość
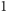 w areale typu A, to
względem większej macierzy jest to pole o wartości
w areale typu A, to
względem większej macierzy jest to pole o wartości
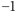 typu D. Podobnie
trzeba obsłużyć inne przejścia.
typu D. Podobnie
trzeba obsłużyć inne przejścia.
W trzech przypadkach – gdy w lewej-górnej ćwiartce otrzymamy
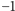 dowolnego typu, w prawej-górnej ćwiartce otrzymamy
dowolnego typu, w prawej-górnej ćwiartce otrzymamy
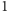 typu B, lub
w lewej-dolnej ćwiartce otrzymamy
typu B, lub
w lewej-dolnej ćwiartce otrzymamy
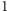 typu C – możemy zakończyć
dalsze obliczenia. Wówczas otrzymujemy areał zamknięty, który zawiera się
całkowicie w aktualnej macierzy.
typu C – możemy zakończyć
dalsze obliczenia. Wówczas otrzymujemy areał zamknięty, który zawiera się
całkowicie w aktualnej macierzy.
Tym razem ćwiczeniem dla Czytelnika pozostanie stwierdzenie, z ilu pól właściwie ten zamknięty areał się składa...
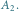 W obszarach obwiedzionych linią czarną znajdują się wartości
W obszarach obwiedzionych linią czarną znajdują się wartości
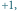 a kolorową
a kolorową
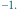 Zakreskowane areały są już zamknięte.
Zakreskowane areały są już zamknięte.