Informatyczny kącik olimpijski
Oszczędny kod
Tematem kolejnej edycji Kącika jest zadanie pochodzące z zeszłorocznej Międzynarodowej Olimpiady Informatycznej o nazwie Oszczędny kod (ang. Saveit).
Problem. Naszym celem jest zakodowanie,
a później odkodowanie pewnych informacji. Musimy zaimplementować
dwie części programu, z których pierwsza otrzyma pewien nieskierowany
spójny graf oraz liczbę
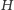 . Jej zadaniem jest wygenerowanie ciągu
bitów. Na podstawie tegoż ciągu, liczby
. Jej zadaniem jest wygenerowanie ciągu
bitów. Na podstawie tegoż ciągu, liczby
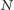 – liczby wierzchołków
grafu – oraz liczby
– liczby wierzchołków
grafu – oraz liczby
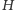 , druga część programu powinna odkodować
interesujące nas informacje, tzn. najkrótsze odległości pomiędzy pewnymi
parami wierzchołków grafu. Wyjaśnijmy teraz, że wierzchołki grafu są
ponumerowane od
, druga część programu powinna odkodować
interesujące nas informacje, tzn. najkrótsze odległości pomiędzy pewnymi
parami wierzchołków grafu. Wyjaśnijmy teraz, że wierzchołki grafu są
ponumerowane od
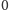 do
do
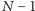 , a interesują nas odległości
wierzchołków o numerach od
, a interesują nas odległości
wierzchołków o numerach od
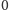 do
do
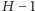 do wszystkich
wierzchołków grafu. Kluczowe w zadaniu jest wygenerowanie możliwie
krótkiego ciągu bitów, który pozwoli na odkodowanie potrzebnych
informacji. Przyjmujemy, że numery wierzchołków (oraz inne liczby
mniejsze niż
do wszystkich
wierzchołków grafu. Kluczowe w zadaniu jest wygenerowanie możliwie
krótkiego ciągu bitów, który pozwoli na odkodowanie potrzebnych
informacji. Przyjmujemy, że numery wierzchołków (oraz inne liczby
mniejsze niż
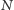 ) możemy zapisać, używając
) możemy zapisać, używając
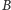 bitów
(czyli w istocie
bitów
(czyli w istocie
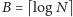 ).
).
Najprostszym sposobem jest po prostu przesłanie całego grafu. Niewątpliwie jest
to wystarczające do uzyskania wszelkich informacji na jego temat. Graf można
przesłać jako liczbę krawędzi, a następnie ich listę. W przypadku, gdy graf jest
pełny, daje to
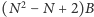 bitów. Można też przesłać macierz
sąsiedztwa, która, naturalnie, zawiera
bitów. Można też przesłać macierz
sąsiedztwa, która, naturalnie, zawiera
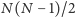 istotnych bitów (mimo
że jest ich łącznie
istotnych bitów (mimo
że jest ich łącznie
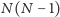 , ale połowę z nich można ustalić,
korzystając z symetryczności tej macierzy).
, ale połowę z nich można ustalić,
korzystając z symetryczności tej macierzy).
Kolejnym pomysłem jest najpierw obliczyć wszystkie interesujące nas
odległości, a następnie zakodować je i przesłać do drugiej części programu.
Interesujących nas liczb jest
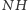 i każda zajmie
i każda zajmie
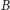 bitów, co da
łącznie
bitów, co da
łącznie
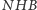 bitów. Jest to dosyć satysfakcjonujące rozwiązanie i było
na Olimpiadzie doceniane połową liczby punktów za to zadanie.
bitów. Jest to dosyć satysfakcjonujące rozwiązanie i było
na Olimpiadzie doceniane połową liczby punktów za to zadanie.
Istnieją jednak lepsze rozwiązania, opierające się na następujących
spostrzeżeniach. Przede wszystkim zwróćmy uwagę na to, jaki jest związek
odległości dwóch sąsiednich wierzchołków
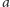 i
i
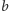 od
ustalonego wierzchołka
od
ustalonego wierzchołka
 . Otóż, nie mogą one różnić się
o więcej niż 1. Weźmy bowiem najkrótsze ścieżki z
. Otóż, nie mogą one różnić się
o więcej niż 1. Weźmy bowiem najkrótsze ścieżki z
 do
tych dwóch wierzchołków, długości
do
tych dwóch wierzchołków, długości
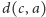 i
i
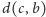 ,
odpowiednio. Oczywiście, moglibyśmy z
,
odpowiednio. Oczywiście, moglibyśmy z
 pójść do
pójść do
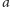 ,
a następnie przejść krawędzią z
,
a następnie przejść krawędzią z
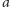 do
do
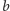 , co dałoby odległość
, co dałoby odległość
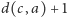 , a skoro długość najkrótszej ścieżki z
, a skoro długość najkrótszej ścieżki z
 do
do
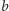 to
to
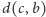 , więc mamy
, więc mamy
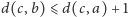 .
Analogicznie w drugą stronę. Różnica między
.
Analogicznie w drugą stronę. Różnica między
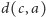 i
i
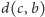 należy więc do zbioru
należy więc do zbioru
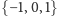 .
.
Aby skorzystać z powyższego faktu, musimy najpierw wiedzieć o jakichś
parach wierzchołków, że są sąsiadami. W związku z tym spójrzmy na
wierzchołek o numerze
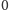 i dla każdego innego wierzchołka
i dla każdego innego wierzchołka
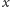 znajdźmy
znajdźmy
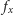 – najbliższy od
– najbliższy od
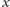 wierzchołek na najkrótszej
ścieżce z
wierzchołek na najkrótszej
ścieżce z
 do
do
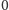 . Zauważmy, że pary
. Zauważmy, że pary
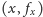 to krawędzie naszego grafu, które tworzą drzewo rozpinające. Na ich
podstawie możemy łatwo wyznaczyć odległości wszystkich wierzchołków
od
to krawędzie naszego grafu, które tworzą drzewo rozpinające. Na ich
podstawie możemy łatwo wyznaczyć odległości wszystkich wierzchołków
od
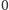 ze wzoru
ze wzoru
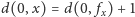 . Zastanówmy się teraz, jak
wyznaczyć odległości od wszystkich wierzchołków z wierzchołka
. Zastanówmy się teraz, jak
wyznaczyć odległości od wszystkich wierzchołków z wierzchołka
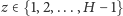 . Przede wszystkim znamy
. Przede wszystkim znamy
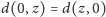 .
Ponadto, dla każdego
.
Ponadto, dla każdego
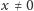 mamy:
mamy:
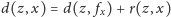 ,
przy czym wiemy już, że
,
przy czym wiemy już, że
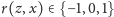 , gdyż
, gdyż
 i
i
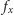 są sąsiadami. W takim razie wystarczy przesłać wszystkie liczby
są sąsiadami. W takim razie wystarczy przesłać wszystkie liczby
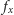 oraz
oraz
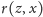 , które zajmują
, które zajmują
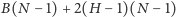 bitów. Dwójka
oznacza tu dwa bity potrzebne na przesłanie liczby ze zbioru
bitów. Dwójka
oznacza tu dwa bity potrzebne na przesłanie liczby ze zbioru
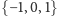 .
.
Ostatnie usprawnienie, wymagane na zawodach do uzyskania maksymalnej noty,
polega na tym, aby zmniejszyć tę właśnie dwójkę do jakiejś mniejszej
stałej. Widzimy bowiem, że nie wykorzystujemy w pełni tych dwóch
bitów, skoro kodujemy na nich tylko trzy różne możliwości, zamiast
dostępnych czterech. Dobrym pomysłem jest spojrzenie na pełen bajt
(tzn. 8 bitów) i spostrzeżenie, że można w nim zakodować
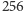 różnych możliwości, a więc w szczególności
różnych możliwości, a więc w szczególności
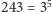 różnych
możliwości, czyli pięć wartości
różnych
możliwości, czyli pięć wartości
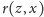 . Stąd dwójkę możemy
mniej więcej zastąpić liczbą
. Stąd dwójkę możemy
mniej więcej zastąpić liczbą
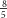 – liczba wykorzystanych bitów
to wówczas
– liczba wykorzystanych bitów
to wówczas
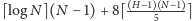 .
.
Zachęcamy Czytelnika do zastanowienia się, czy do rozwiązania zadania
wystarczy użyć
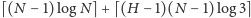 bitów
(zauważmy, że nie jest to wielka poprawka, gdyż
bitów
(zauważmy, że nie jest to wielka poprawka, gdyż
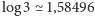 ).
Warto także zastanowić się, jak szybko działają wszystkie opisane wyżej
rozwiązania.
).
Warto także zastanowić się, jak szybko działają wszystkie opisane wyżej
rozwiązania.