Od paraboli do podziału sekretu
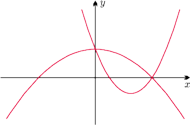
Zaczniemy od przypomnienia kilku podstawowych własności wielomianów
nad liczbami rzeczywistymi. Skupmy się najpierw na funkcji kwadratowej
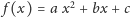 . Będzie nas interesowało to, ile informacji
potrzebujemy, żeby ustalić parametry
. Będzie nas interesowało to, ile informacji
potrzebujemy, żeby ustalić parametry
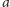 ,
,
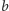 i
i
 .
Na przykład, jeśli znamy dwa punkty
.
Na przykład, jeśli znamy dwa punkty
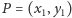 ,
,
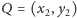 ,
przez które przechodzi szukana „szkolna” parabola, to wiemy jeszcze zbyt mało.
Co to znaczy? Weźmy dla przykładu
,
przez które przechodzi szukana „szkolna” parabola, to wiemy jeszcze zbyt mało.
Co to znaczy? Weźmy dla przykładu
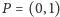 oraz
oraz
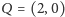 .
Łatwo sprawdzić, że zarówno funkcja
.
Łatwo sprawdzić, że zarówno funkcja
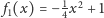 , jak i
, jak i
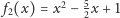 spełniają nasze oczekiwania, tzn. oba punkty leżą na
wykresach obu funkcji. Okazuje się, że zawężenie kryteriów do trzech
punktów sprawia, iż znajdziemy co najwyżej jedno rozwiązanie. Faktu tego
nie będziemy ściśle dowodzić, intuicja powinna jednak podpowiadać, że
właśnie trzy punkty są konieczne i wystarczające. Dlaczego? Jeden punkt
przekłada się na jedno równanie liniowe z trzema niewiadomymi
spełniają nasze oczekiwania, tzn. oba punkty leżą na
wykresach obu funkcji. Okazuje się, że zawężenie kryteriów do trzech
punktów sprawia, iż znajdziemy co najwyżej jedno rozwiązanie. Faktu tego
nie będziemy ściśle dowodzić, intuicja powinna jednak podpowiadać, że
właśnie trzy punkty są konieczne i wystarczające. Dlaczego? Jeden punkt
przekłada się na jedno równanie liniowe z trzema niewiadomymi
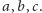 Trzy takie punkty dają trzy równania.
Trzy takie punkty dają trzy równania.
Podana wyżej własność funkcji kwadratowej uogólnia się na wielomiany wyższych stopni. Sformułujemy odpowiednie twierdzenie.
Twierdzenie 1. Jeśli
liczby rzeczywiste
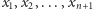 są parami różne, to przez ustalone
punkty
są parami różne, to przez ustalone
punkty
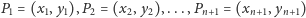 przechodzi
wykres dokładnie jednego wielomianu (tzw. wielomianu Lagrange’a) nad
liczbami rzeczywistymi stopnia co najwyżej
przechodzi
wykres dokładnie jednego wielomianu (tzw. wielomianu Lagrange’a) nad
liczbami rzeczywistymi stopnia co najwyżej
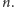
Możemy to uogólnić. Otóż twierdzenie jest wciąż prawdziwe, jeśli
zmienimy zbiór, nad którym rozpatrywane są wielomiany. Przykładowo,
w świecie liczb zespolonych to również jest prawdą. Dla osób zaznajomionych
z podstawami algebry będzie jasne, jeśli powiemy, że jest ono prawdziwe nad
każdym ciałem. Dla naszych rozważań nie będzie potrzebna dokładna
definicja tej struktury. Zajmiemy się jednym konkretnym przykładem. Otóż
niech
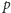 będzie liczbą pierwszą oraz niech
będzie liczbą pierwszą oraz niech
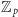 będzie zbiorem liczb
naturalnych od
będzie zbiorem liczb
naturalnych od
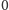 do
do
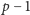 . Skojarzymy z tym zbiorem działania
dodawania i mnożenia. Przyjmiemy, że aby dodać dwie liczby z tego zbioru,
dodajemy je w sposób tradycyjny, po czym jako wynik bierzemy resztę
z dzielenia przez
. Skojarzymy z tym zbiorem działania
dodawania i mnożenia. Przyjmiemy, że aby dodać dwie liczby z tego zbioru,
dodajemy je w sposób tradycyjny, po czym jako wynik bierzemy resztę
z dzielenia przez
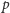 . Dla mnożenia robimy analogicznie. Poniższy
przykład ilustruje te definicje dla
. Dla mnożenia robimy analogicznie. Poniższy
przykład ilustruje te definicje dla
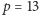 :
:

Nad taką dziwaczną strukturą będziemy badać tradycyjne wielomiany. Ponownie
przyjmijmy
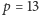 oraz
oraz
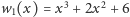 ,
,
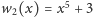 ,
,
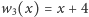 . Mamy wówczas przykładowo:
. Mamy wówczas przykładowo:

Jak uprzedziliśmy, w tym świecie również zachodzi twierdzenie o wielomianach.
Twierdzenie 2. Jeśli elementy
ciała
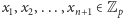 są parami różne, to przez ustalone punkty
są parami różne, to przez ustalone punkty
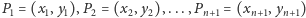 przechodzi wykres dokładnie jednego wielomianu nad
przechodzi wykres dokładnie jednego wielomianu nad
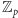 stopnia
co najwyżej
stopnia
co najwyżej
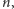 o ile
o ile
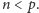
A gdzie w tym wszystkim podział sekretu? Jeszcze chwila cierpliwości i wszystko się wyjaśni. Mamy już potrzebny aparat matematyczny, czas więc na ogólne wprowadzenie w problematykę sekretów, spisków i wzajemnej nieufności.
Rozważmy uproszczoną sytuację: pewna grupa
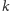 osób ma
jakiś wspólny sekret
osób ma
jakiś wspólny sekret
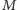 , który interpretujemy jako jedną liczbę
z zakresu
, który interpretujemy jako jedną liczbę
z zakresu
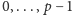 , czy raczej – mówiąc językiem algebry –
jako element ciała
, czy raczej – mówiąc językiem algebry –
jako element ciała
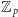 . Chcemy jakoś rozdzielić informację
o
. Chcemy jakoś rozdzielić informację
o
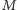 wśród grupy, aby uzyskać następujący poziom bezpieczeństwa
sekretu
wśród grupy, aby uzyskać następujący poziom bezpieczeństwa
sekretu
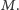
Definicja (Poziom bezpieczeństwa 1). Dowolna podgrupa
licząca
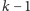 osób nie jest w stanie odtworzyć sekretu
osób nie jest w stanie odtworzyć sekretu
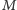 na
podstawie informacji posiadanych przez członków podgrupy. Pełna grupa
na
podstawie informacji posiadanych przez członków podgrupy. Pełna grupa
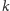 osób jest w stanie odtworzyć
osób jest w stanie odtworzyć
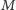 .
.
Wróćmy do świata wielomianów. Niech
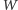 będzie losowym
wielomianem nad
będzie losowym
wielomianem nad
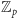 stopnia
stopnia
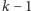 , takim że
, takim że
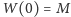 .
Tylko ten wielomian będzie nam potrzebny, aby rozdzielić sekret. Pierwszej
osobie zdradzimy wartość
.
Tylko ten wielomian będzie nam potrzebny, aby rozdzielić sekret. Pierwszej
osobie zdradzimy wartość
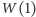 , drugiej –
, drugiej –
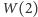 itd.
Ostatnia osoba pozna
itd.
Ostatnia osoba pozna
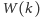 . Teraz z twierdzenia 2 wynika, że
informacje posiadane przez te osoby pozwalają odtworzyć wielomian, a więc
i obliczyć
. Teraz z twierdzenia 2 wynika, że
informacje posiadane przez te osoby pozwalają odtworzyć wielomian, a więc
i obliczyć
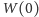 , to znaczy poznać sekret
, to znaczy poznać sekret
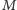 . Gdy zabraknie
choć jednej osoby, to wielomian nie jest wyznaczony jednoznacznie
i wiadomość pozostaje tajna.
. Gdy zabraknie
choć jednej osoby, to wielomian nie jest wyznaczony jednoznacznie
i wiadomość pozostaje tajna.
Co tu jest jeszcze do dowiedzenia?
Powyższe rozumowanie zawiera, oczywiście, pewne uproszczenia.
W szczególności nie wskazaliśmy, jak wykazać, że żadne
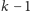 osób nie może odtworzyć
osób nie może odtworzyć
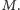 Nie będziemy wszystkiego uzupełniać.
Chcemy jednak dokładnie określić, czego należałoby ściśle dowieść, aby
móc stwierdzić, że opisany schemat jest bezpieczny.
Nie będziemy wszystkiego uzupełniać.
Chcemy jednak dokładnie określić, czego należałoby ściśle dowieść, aby
móc stwierdzić, że opisany schemat jest bezpieczny.
Przede wszystkim nie zdefiniowaliśmy precyzyjnie, co rozumiemy przez
sformułowanie, że wiadomość jest tajna. Nie wystarczy powiedzieć,
że posiadana wiedza nie wystarcza do jednoznacznego odtworzenia
sekretu
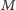 . Mogłoby się przecież tak zdarzyć, że – w skrajnym
przypadku – niejednoznaczność polega na tym, iż mamy dwóch
kandydatów na
. Mogłoby się przecież tak zdarzyć, że – w skrajnym
przypadku – niejednoznaczność polega na tym, iż mamy dwóch
kandydatów na
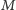 . Pierwsze przybliżenie definicji mogłoby więc
iść w tę właśnie stronę. To znaczy chcielibyśmy, aby posiadana
wiedza nie mogła wykluczyć żadnego kandydata na
. Pierwsze przybliżenie definicji mogłoby więc
iść w tę właśnie stronę. To znaczy chcielibyśmy, aby posiadana
wiedza nie mogła wykluczyć żadnego kandydata na
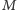 . Jednak
również i taka definicja jest za słaba. Nie wyklucza bowiem przypadku, gdy
posiadana wiedza pozwala stwierdzić, że, na przykład,
. Jednak
również i taka definicja jest za słaba. Nie wyklucza bowiem przypadku, gdy
posiadana wiedza pozwala stwierdzić, że, na przykład,
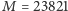 z prawdopodobieństwem
z prawdopodobieństwem
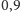 (a nie
(a nie
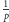 , jak pewnie byśmy
oczekiwali). Najsilniejsza definicja jest sformułowana właśnie w języku
probabilistyki: dana wiadomość jest tajna, jeśli posiadana wiedza nie pozwala
na ustalenie innego rozkładu prawdopodobieństw tajnego sekretu niż rozkład
jednostajny.
, jak pewnie byśmy
oczekiwali). Najsilniejsza definicja jest sformułowana właśnie w języku
probabilistyki: dana wiadomość jest tajna, jeśli posiadana wiedza nie pozwala
na ustalenie innego rozkładu prawdopodobieństw tajnego sekretu niż rozkład
jednostajny.
Okazuje się, że dzielenie sekretu za pomocą wielomianu spełnia tę najsilniejszą definicję. Zachęcamy do udowodnienia tego faktu, a przynajmniej dokładnego sformułowania, co tak naprawdę trzeba udowodnić.
Dalsze zastosowania
Wielomiany dają nam jeszcze inne ciekawe możliwości (ponownie
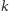 oznacza liczbę osób).
oznacza liczbę osób).
Definicja (Poziom bezpieczeństwa 2). Dowolna podgrupa
 osób nie jest w stanie odtworzyć
osób nie jest w stanie odtworzyć
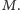 Każda podgrupa
Każda podgrupa
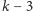 osób jest w stanie odtworzyć sekret
osób jest w stanie odtworzyć sekret
Powyższe bezpieczeństwo uzyskujemy, na przykład, następująco: losujemy
wielomian stopnia
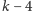 o wartości
o wartości
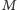 w zerze. Osobom dajemy
kolejne wartości
w zerze. Osobom dajemy
kolejne wartości
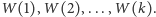 Ponownie twierdzenie 2
dowodzi tezy. Liczba
Ponownie twierdzenie 2
dowodzi tezy. Liczba
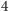 została tu wybrana przykładowo, można wybrać
dowolną inną. Oczywiście, żeby zachować pełną ścisłość, należy
udowodnić trudniejszy fakt dotyczący rozkładu prawdopodobieństw.
została tu wybrana przykładowo, można wybrać
dowolną inną. Oczywiście, żeby zachować pełną ścisłość, należy
udowodnić trudniejszy fakt dotyczący rozkładu prawdopodobieństw.
To jednak nie koniec. Jako ostatnią rzecz proponujemy ćwiczenie. Zachęcamy Czytelnika do pokazania, jak użyć techniki wielomianów, aby osiągnąć następujący poziom bezpieczeństwa (dla Czytelnika Leniwego rozwiązanie jest w dymku).
Definicja (Poziom bezpieczeństwa 3). Niech
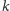 oznacza liczbę
pięcioosobowych rozłącznych grup osób. Chcemy, aby do poznania sekretu
konieczna była większość a więc co najmniej trzy osoby z co najmniej
oznacza liczbę
pięcioosobowych rozłącznych grup osób. Chcemy, aby do poznania sekretu
konieczna była większość a więc co najmniej trzy osoby z co najmniej
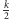 grup.
grup.
Opisany w artykule pomysł dzielenia sekretu zawdzięczamy izraelskiemu kryptografowi Adiemu Shamirowi. Zainteresowanych zachęcamy do samodzielnych poszukiwań i dalszego zgłębiania tej tematyki.
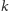 osób i dla wymagania, że do
odzyskania sekretu potrzebnych jest
osób i dla wymagania, że do
odzyskania sekretu potrzebnych jest
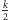 osób. Następnie uzyskane punkty
traktujemy jako kolejne sekrety, które w obrębie grupy ponownie szyfrujemy
za pomocą tej samej techniki, ale tym razem dla pięciu osób łącznie i trzech
potrzebnych do odszyfrowania.
osób. Następnie uzyskane punkty
traktujemy jako kolejne sekrety, które w obrębie grupy ponownie szyfrujemy
za pomocą tej samej techniki, ale tym razem dla pięciu osób łącznie i trzech
potrzebnych do odszyfrowania.