Informatyczny kącik olimpijski
Słownik przekątnych
W tym odcinku zajmiemy się zadaniem, które zamiast na zawodach, pojawiło się na... kolokwium (z Algorytmów i Struktur Danych). Stanowiłoby ono bardzo ładne zadanie na zawodach.

Rys. 1 Kilka przekątnych ośmiokąta reprezentowanych jako łuki. Wartością
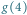 jest łuk
jest łuk
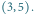

Rys. 2 Tak wyobrażamy sobie drzewo przedziałowe.
Od czego zacząć? Na początek może ułatwimy sobie zadanie — zauważmy,
że wielokąt z zadania można „wygiąć” na płaszczyźnie, aż wierzchołki
utworzą ciąg punktów na prostej, ponumerowanych od
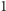 do
do
 ,
a przekątne zamienią się na łuki (jak na rysunku 1). Resztę zadania łatwo
przetłumaczyć do tej nowej wersji. W tym momencie już pojawia się
pomysł — może uda się użyć drzewa przedziałowego? Ale zanim
napiszemy jak, wyjaśnijmy sobie, co będziemy rozumieć przez drzewo
przedziałowe.
,
a przekątne zamienią się na łuki (jak na rysunku 1). Resztę zadania łatwo
przetłumaczyć do tej nowej wersji. W tym momencie już pojawia się
pomysł — może uda się użyć drzewa przedziałowego? Ale zanim
napiszemy jak, wyjaśnijmy sobie, co będziemy rozumieć przez drzewo
przedziałowe.
Drzewo przedziałowe (rys. 2) służy do przechowywania informacji związanych
z podprzedziałami zadanego przedziału
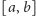 . W korzeniu drzewa jest
zapisana informacja związana z całym przedziałem, w jego dwóch synach
informacje związane z lewą i prawą połową tego przedziału i tak dalej, aż
wreszcie w liściach zapamiętywane są wartości odpowiadające pojedynczym
punktom. Wartość przechowywaną w wierzchołku
. W korzeniu drzewa jest
zapisana informacja związana z całym przedziałem, w jego dwóch synach
informacje związane z lewą i prawą połową tego przedziału i tak dalej, aż
wreszcie w liściach zapamiętywane są wartości odpowiadające pojedynczym
punktom. Wartość przechowywaną w wierzchołku
 będziemy
oznaczać
będziemy
oznaczać
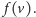
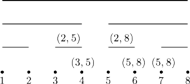
Rys. 3 Zawartość drzewa przedziałowego po wstawieniu przekątnych z rysunku 1.
Jako ćwiczenie Czytelnik może w oparciu o drzewo przedziałowe skonstruować strukturę danych do obsługi dynamicznie zmieniającego się ciągu
, dopuszczającą operacje (1) inicjuj wszystkie wyrazy na
, (2) ustaw
oraz (3) podaj sumę podciągu
. Operacje (2) i (3) powinny działać w czasie
.
No dobrze, ale jak to zastosować do naszego problemu?
Zapytajmy, kiedy w nowym modelu (tym z prostą), można połączyć dwa
punkty
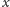 i
i
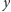 przekątną? Spójrzmy na rysunek 1. Dla danego
przekątną? Spójrzmy na rysunek 1. Dla danego
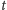 niech
niech
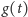 oznacza najniższy łuk, który przecina pionowa
półprosta wychodząca z punktu
oznacza najniższy łuk, który przecina pionowa
półprosta wychodząca z punktu
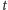 (dotknięcie nie liczy się jako przecięcie;
wartością
(dotknięcie nie liczy się jako przecięcie;
wartością
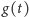 może być „pusty” łuk). Łuk od
może być „pusty” łuk). Łuk od
 do
do
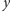 można dodać dokładnie wtedy, gdy
można dodać dokładnie wtedy, gdy
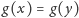 . Musimy więc
szybko obliczać wartości funkcji
. Musimy więc
szybko obliczać wartości funkcji
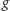 . Do tego przyda się drzewo
przedziałowe.
. Do tego przyda się drzewo
przedziałowe.
Przypuśćmy, że wiemy już, iż możemy dodać przekątną
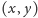 . Jak to zrobić? Otóż przekątna „pokryje” podciąg wierzchołków
. Jak to zrobić? Otóż przekątna „pokryje” podciąg wierzchołków
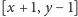 . Słowo pokryje oznacza, że półprosta wychodząca
z każdego z wierzchołków z tego przedziału przetnie naszą przekątną, choć
niekoniecznie jako pierwszą.
. Słowo pokryje oznacza, że półprosta wychodząca
z każdego z wierzchołków z tego przedziału przetnie naszą przekątną, choć
niekoniecznie jako pierwszą.
Funkcja dodająca przekątną
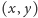 będzie działać rekurencyjnie.
Najpierw wywołujemy ją dla korzenia. Dodając przekątną
będzie działać rekurencyjnie.
Najpierw wywołujemy ją dla korzenia. Dodając przekątną
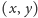 w wierzchołku
w wierzchołku
 drzewa przedziałowego, wykonujemy operacje:
drzewa przedziałowego, wykonujemy operacje:
- •
- jeśli podprzedział z wierzchołka
 zawiera się w
zawiera się w
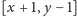 , to ustaw
, to ustaw
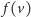 na niższy
z łuków
na niższy
z łuków
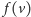 i
i
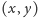 (wysokość łuku można szybko
obliczyć, jest to
(wysokość łuku można szybko
obliczyć, jest to
 ),
),
- •
- jeśli podprzedział z wierzchołka
 jest rozłączny
z
jest rozłączny
z
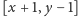 , to nic nie rób,
, to nic nie rób,
- •
- w przeciwnym razie wywołaj funkcję
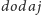 dla dzieci wierzchołka
dla dzieci wierzchołka
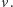
Łatwo zauważyć, że
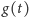 to najniższy spośród łuków
zapamiętanych w wierzchołkach drzewa odpowiadających przedziałom
pokrywającym punkt
to najniższy spośród łuków
zapamiętanych w wierzchołkach drzewa odpowiadających przedziałom
pokrywającym punkt
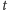 , czyli na ścieżce prowadzącej z korzenia
do wierzchołka
, czyli na ścieżce prowadzącej z korzenia
do wierzchołka
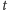 . Zatem
. Zatem
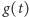 można znaleźć w czasie
można znaleźć w czasie
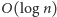 .
.
Funkcja Sprawdź może działać na podobnej zasadzie, sprawdzając, czy w odwiedzanych po drodze wierzchołkach jest zapamiętana poszukiwana przekątna. (Każda wstawiona przekątna zostaje gdzieś zapamiętana, dlaczego?)
Aktualizację stanu struktury podczas usuwania przekątnej pozostawiamy Czytelnikowi.
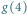 jest łuk
jest łuk