Przede wszystkim zauważmy, że powyższe wymagania ograniczające możliwości wyboru stolic możemy zamienić na zestaw zdań logicznych. Dla każdego miasta 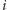 wprowadźmy zmienną logiczną 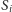oznaczającą, czy dane miasto jest stolicą swojego województwa. Wówczas drogę łączącą miasta 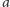 i 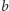 możemy rozumieć jako alternatywę 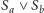. Województwo interpretujemy natomiast jako zbiór alternatyw postaci 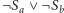dla każdej pary różnych miast ,  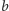z tego województwa.

W ten sposób sprowadziliśmy zadanie do wybrania dla każdego miasta 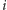 wartości zmiennej logicznej 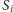 , tak aby zachodziły wszystkie wymienione wyżej alternatywy. (Jeżeli znajdziemy rozwiązanie, w którym pewne województwo nie ma żadnej stolicy, to w takim przypadku możemy dowolne jego miasto uznać za jego stolicę i nie zepsuje to znalezionego rozwiązania.) Jest to klasyczny problem 2-SAT, dla którego znany jest liniowy (dokładniej: liniowo zależny od liczby zmiennych i liczby alternatyw) algorytm. W przypadku naszego zadania oznacza to rozwiązanie w czasie 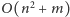. Nie jest to jeszcze wynik satysfakcjonujący. Aby go poprawić, zagłębimy się w działanie algorytmu rozwiązującego problem 2-SAT, po czym spróbujemy go przyspieszyć dla tego konkretnego zadania.

Zauważmy, że każdą alternatywę 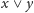możemy zamienić na dwie implikacje: 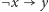oraz 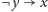. Zbudujemy zatem graf, którego wierzchołkami są 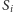 oraz 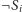 dla wszystkich 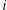 , a krawędziami – implikacje powstałe ze wszystkich naszych alternatyw. Chcemy dla każdego miasta 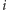 wybrać dokładnie jeden z dwóch odpowiadających mu wierzchołków i uznać za prawdziwy, pamiętając przy tym o implikacjach. Nietrudno spostrzec, że w każdej silnie spójnej składowej takiego grafu wszystkie wierzchołki mają taką samą wartość logiczną. Jeśli utożsamimy wierzchołki należące do tych samych silnie spójnych składowych, otrzymujemy tzw. graf silnie spójnych składowych, w którym nie ma już cykli. Ten graf sortujemy topologicznie. Rozpatrujemy kolejno te silnie spójne składowe, z których wychodzą krawędzie tylko do już rozpatrzonych. Zauważmy, że jeśli  i 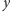 są w tej samej silnie spójnej składowej, to 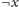 i 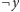 także, gdyż jeśli z   można dojść krawędziami do 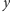 , to z 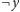  można analogicznie dojść do 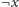 , podobnie jeśli można dojść z 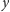  do 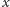 , to można z 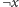  do 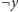 (wynika to ze sposobu konstrukcji krawędzi z alternatyw). W takim razie, podczas rozpatrywania kolejnych składowych, jeśli napotykamy taką, której komplementarna nie została jeszcze rozpatrzona, ustalamy, że wszystkie wierzchołki tej składowej będą prawdziwe, a komplementarnej – fałszywe. W ten sposób dla każdej pary literałów 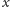,  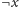zdecydujemy, który z nich jest prawdziwy, a wszystkie implikacje, a więc także alternatywy, będą spełnione (dlaczego?). Jedynym przypadkiem, gdy ta metoda nie działa, jest sytuacja, gdy dla pewnego 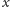 ,  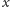i 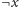  leżą w jednej silnie spójnej składowej. W takim przypadku w ogóle nie istnieje żadne rozwiązanie, gdyż implikacje są sprzeczne.

Widzimy, że główny koszt czasowy algorytmu jest generowany przez znajdowanie silnie spójnych składowych i grafu tychże oraz przez sortowanie topologiczne tego grafu. Wszystkie te operacje w standardowy sposób wykonujemy za pomocą dwóch przeszukiwań w głąb (DFS). Koszt jednego takiego przeszukiwania to 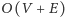, gdzie 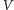to liczba wierzchołków, a 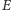  – liczba krawędzi grafu. 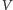 jest w naszym przypadku równe 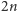 , a więc akceptowalne. Problemem jest 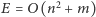. Krawędzie odpowiadające niewygodnemu składnikowi 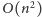 są jednak rozmieszczone regularnie wewnątrz poszczególnych województw. Możemy zatem pamiętać dla każdego wierzchołka jedynie jego „normalnych” sąsiadów, natomiast krawędzie wynikające z przynależności do województwa wyznaczać na bieżąco, w razie potrzeby. Będąc w dowolnym wierzchołku, możemy pójść w przeszukiwaniu grafu dowolną krawędzią z jego listy krawędzi lub też krawędzią z listy krawędzi województwa. Co do tych ostatnich, to jeśli zużywamy krawędź „wojewódzką” z 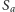  do 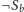 , możemy spokojnie założyć, że krawędzie „wojewódzkie” z 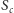  do 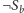 dla wszystkich  są już niepotrzebne, i o nich zapomnieć. Jest tak, gdyż wierzchołek 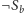odwiedzamy raz, idąc z 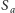 , a wszystkie pozostałe krawędzie do niego prowadzące już nam nie posłużą w przeszukiwaniu. Jeśli rozmiar województwa to 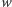 , to zamiast 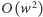 krawędzi dla tego województwa pamiętamy tylko 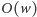 końców tych krawędzi i każdy koniec wykorzystujemy dokładnie raz, przy pierwszej nadarzającej się okazji.

W ten sposób wykonujemy przeszukiwanie DFS w rozważanym grafie w czasie 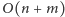. Całe rozwiązanie ma złożoność czasową i pamięciową .
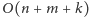