Informatyczny kącik olimpijski
Ogromna wieża
Tym razem przyjrzymy się zadaniu Ogromna wieża (ang. A huge tower) pochodzącemu z Olimpiady Informatycznej Europy Środkowej 2010 (CEOI 2010).
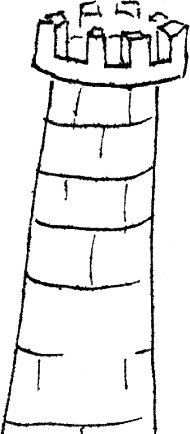
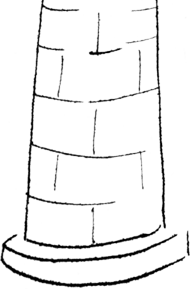
Oznaczmy przez
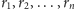 rozmiary poszczególnych bloków,
a wieżę zbudowaną z nich zgodnie z warunkami zadania nazwijmy
poprawną. Pierwsze rozwiązanie, które przedstawimy, jest najmniej
efektywne, ale nie wymaga żadnych spostrzeżeń. Wystarczy użyć
programowania dynamicznego do stopniowego obliczania wartości
rozmiary poszczególnych bloków,
a wieżę zbudowaną z nich zgodnie z warunkami zadania nazwijmy
poprawną. Pierwsze rozwiązanie, które przedstawimy, jest najmniej
efektywne, ale nie wymaga żadnych spostrzeżeń. Wystarczy użyć
programowania dynamicznego do stopniowego obliczania wartości
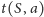 , które oznaczają odpowiedź na pytanie „na ile sposobów
można zbudować poprawną wieżę z bloków należących do zbioru
, które oznaczają odpowiedź na pytanie „na ile sposobów
można zbudować poprawną wieżę z bloków należących do zbioru
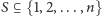 , tak aby blok o numerze
, tak aby blok o numerze
 znalazł się na dole?”.
Naturalnie, zakładamy, że
znalazł się na dole?”.
Naturalnie, zakładamy, że
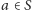 . Jeśli dostępny jest tylko jeden
blok, wieżę można zbudować na dokładnie jeden sposób. Jeśli zaś
mamy zbiór
. Jeśli dostępny jest tylko jeden
blok, wieżę można zbudować na dokładnie jeden sposób. Jeśli zaś
mamy zbiór
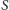 co najmniej dwóch bloków, a blok
co najmniej dwóch bloków, a blok
 ma
znaleźć się na dole, to należy na wszystkie sposoby wybrać blok, który
ma się znaleźć bezpośrednio na nim. Jeśli ten przedostatni blok
oznaczymy przez
ma
znaleźć się na dole, to należy na wszystkie sposoby wybrać blok, który
ma się znaleźć bezpośrednio na nim. Jeśli ten przedostatni blok
oznaczymy przez
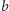 , to pod warunkiem, że
, to pod warunkiem, że
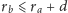 ,
znaleźliśmy
,
znaleźliśmy
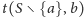 sposobów na zbudowanie naszej
wieży. Sumujemy takie wartości po wszystkich możliwościach wyboru
sposobów na zbudowanie naszej
wieży. Sumujemy takie wartości po wszystkich możliwościach wyboru
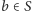 i otrzymujemy
i otrzymujemy
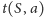 . W ten sposób, szukając odpowiedzi
w kolejności od najmniej licznych zbiorów
. W ten sposób, szukając odpowiedzi
w kolejności od najmniej licznych zbiorów
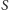 , każdą z nich
znajdujemy w czasie proporcjonalnym do rozmiaru
, każdą z nich
znajdujemy w czasie proporcjonalnym do rozmiaru
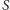 , co oznacza,
że cały problem zostanie rozwiązany po wykonaniu
, co oznacza,
że cały problem zostanie rozwiązany po wykonaniu
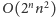 operacji.
operacji.
Aby znaleźć bardziej efektywne rozwiązanie, warto inaczej pomyśleć
o budowaniu wieży. Zamiast zastanawiać się, który z bloków położymy na
spód albo wierzch, rozpatrujmy bloki kolejno, od najmniejszego do największego,
ale za to dopuśćmy umieszczanie kolejnego bloku gdzieś w środku już
zbudowanej konstrukcji. Załóżmy, że rozmiary bloków
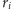 są
uporządkowane niemalejąco, i rozważmy dowolną poprawną wieżę
zbudowaną z bloków o numerach od
są
uporządkowane niemalejąco, i rozważmy dowolną poprawną wieżę
zbudowaną z bloków o numerach od
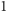 do
do
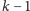 . Powiedzmy, że
w tej wieży blok
. Powiedzmy, że
w tej wieży blok
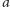 leży pod blokiem
leży pod blokiem
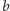 i pomiędzy nie chcemy
teraz włożyć blok
i pomiędzy nie chcemy
teraz włożyć blok
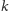 . Zastanówmy się, kiedy nowa konstrukcja jest
poprawna. Poza fragmentem zawierającym bloki
. Zastanówmy się, kiedy nowa konstrukcja jest
poprawna. Poza fragmentem zawierającym bloki
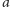 ,
,
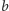 i
i
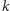 ,
nowa wieża jest poprawna wtedy i tylko wtedy, gdy dotychczasowa była.
Ponadto, musi być
,
nowa wieża jest poprawna wtedy i tylko wtedy, gdy dotychczasowa była.
Ponadto, musi być
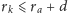 oraz
oraz
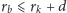 . Pamiętajmy jednak,
że
. Pamiętajmy jednak,
że
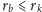 , więc druga nierówność zawsze zachodzi. To znaczy, że
jeżeli mamy poprawną wieżę zbudowaną z bloków
, więc druga nierówność zawsze zachodzi. To znaczy, że
jeżeli mamy poprawną wieżę zbudowaną z bloków
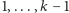 oraz
oraz
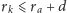 , to wstawiając blok
, to wstawiając blok
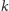 między
między
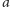 oraz
oraz
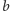 ,
otrzymamy poprawną wieżę dla bloków
,
otrzymamy poprawną wieżę dla bloków
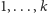 . Z drugiej strony, jeśli
mamy poprawną wieżę dla bloków
. Z drugiej strony, jeśli
mamy poprawną wieżę dla bloków
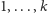 i blok
i blok
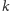 znajduje się
w niej między blokami
znajduje się
w niej między blokami
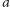 oraz
oraz
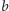 , to
, to
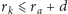 . Ponieważ
jednak
. Ponieważ
jednak
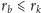 , więc mamy
, więc mamy
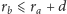 i rozważana wieża
po usunięciu bloku
i rozważana wieża
po usunięciu bloku
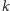 staje się poprawną wieżą dla bloków
staje się poprawną wieżą dla bloków
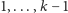 .
.
Z powyższego rozumowania wyciągamy wniosek, że wieża ze wstawionym
pomiędzy bloki
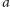 i
i
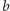 blokiem
blokiem
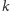 (nie mniejszym od
wszystkich bloków wieży) jest poprawna wtedy i tylko wtedy, gdy była
poprawna bez niego oraz gdy można go położyć na bloku
(nie mniejszym od
wszystkich bloków wieży) jest poprawna wtedy i tylko wtedy, gdy była
poprawna bez niego oraz gdy można go położyć na bloku
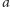 . Bardzo
ważne jest spostrzeżenie, że w tym właśnie wniosku nie używamy tak
naprawdę rozmiarów bloków innych niż
. Bardzo
ważne jest spostrzeżenie, że w tym właśnie wniosku nie używamy tak
naprawdę rozmiarów bloków innych niż
 oraz
oraz
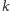 .
.
Z takim spostrzeżeniem możemy śmiało konstruować algorytm
rozwiązujący nasz problem. Oznaczmy przez
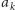 liczbę tych bloków
spośród
liczbę tych bloków
spośród
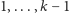 , na które można położyć blok
, na które można położyć blok
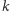 . Każdy
blok można też położyć na samym dole wieży. Widzimy, że używając
tylko pierwszego bloku, poprawną wieżę można zbudować na
. Każdy
blok można też położyć na samym dole wieży. Widzimy, że używając
tylko pierwszego bloku, poprawną wieżę można zbudować na
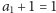 sposób. Używając pierwszych dwóch, na
sposób. Używając pierwszych dwóch, na
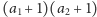 sposobów.
I tak dalej: aby utworzyć poprawną wieżę z
sposobów.
I tak dalej: aby utworzyć poprawną wieżę z
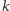 pierwszych bloków,
należy jakoś zbudować wieżę z pierwszych
pierwszych bloków,
należy jakoś zbudować wieżę z pierwszych
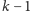 bloków,
a następnie na jeden z
bloków,
a następnie na jeden z
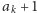 sposobów ustawić blok
sposobów ustawić blok
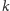 .
Ostatecznym wynikiem jest więc
.
Ostatecznym wynikiem jest więc
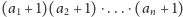 .
Zauważmy jeszcze, że wartości
.
Zauważmy jeszcze, że wartości
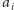 możemy szybko obliczyć,
korzystając z (niemalejącego) ciągu
możemy szybko obliczyć,
korzystając z (niemalejącego) ciągu
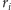 . Używamy do tego dwóch
indeksów,
. Używamy do tego dwóch
indeksów,
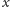 oraz
oraz
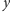 , przy czym
, przy czym
 przebiega kolejno
wartości od
przebiega kolejno
wartości od
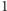 do
do
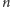 , a
, a
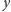 ma być zawsze najmniejszym
takim indeksem, że
ma być zawsze najmniejszym
takim indeksem, że
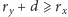 . W takim przypadku mamy, dla każdego
kolejno rozpatrywanego
. W takim przypadku mamy, dla każdego
kolejno rozpatrywanego
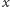 , równość
, równość
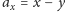 . Dodajmy, że
oba wskaźniki w trakcie działania tego algorytmu jedynie wzrastają, co
zapewnia, że czas obliczenia ciągu
. Dodajmy, że
oba wskaźniki w trakcie działania tego algorytmu jedynie wzrastają, co
zapewnia, że czas obliczenia ciągu
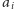 jest liniowy. Całkowity
koszt czasowy jest więc uzależniony od sortowania rozmiarów bloków
i wynosi
jest liniowy. Całkowity
koszt czasowy jest więc uzależniony od sortowania rozmiarów bloków
i wynosi
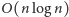 .
.