W informatycznym kąciku olimpijskim w poprzednim numerze Delty opisane zostało zadanie, którego rozwiązanie sprowadzono do obliczenia pewnej liczby współczynników dwumianowych modulo ustalony moduł  . Przedstawiono tam też prosty algorytm obliczania wartości 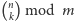, działający w czasie 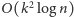, zatem niezbyt praktyczny, gdy zarówno  , jak i 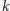 są duże. W niniejszym artykule przedstawimy inny algorytm, który po fazie obliczeń wstępnych zajmujących czas 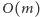 pozwoli na obliczanie 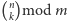w czasie 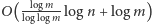. Na początku pokażemy, jak obliczać współczynniki dwumianowe modulo potęga liczby pierwszej. 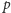W dalszej części artykułu  zawsze będzie oznaczać liczbę pierwszą, a 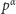  jej potęgę o wykładniku całkowitym dodatnim.

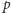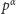Na początku pokażemy, jak obliczać współczynniki dwumianowe modulo potęga liczby pierwszej. W dalszej części artykułu  zawsze będzie oznaczać liczbę pierwszą, a   jej potęgę o wykładniku całkowitym dodatnim.

Aby obliczyć 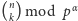, skorzystamy ze wzoru

i spróbujemy sprowadzić zadanie do obliczenia 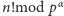. Musimy jednak uważać, gdyż np. dla 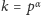w mianowniku pojawia nam się zero. Aby poradzić sobie z tym kłopotem, wyciągniemy z silni wszystkie czynniki 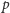 . Niech mianowicie 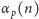będzie największą potęgą liczby 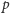 dzielącą 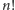 . Jeśli będziemy umieli znaleźć liczbę

to rozwiązaniem będzie

Dzielenie w powyższym wzorze jest wykonywane w grupie  .

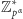Czytelnicy znający rozwiązanie zadania ,,obliczyć, iloma zerami kończy się zapis dziesiętny liczby 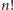 ” wiedzą, a pozostali łatwo się przekonają, że

zatem 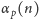możemy łatwo obliczyć w czasie 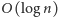. Pozostaje już tylko znaleźć wartość 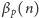 . Zdefiniujmy silniopodobną funkcję 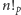 oznaczającą iloczyn liczb od 1 do 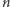 niepodzielnych przez 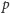 . Wprowadźmy też oznaczenie

Przypomnijmy, że twierdzenie Wilsona orzeka, że dla liczby pierwszej 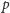 spełnione jest 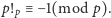Uogólnienie tego twierdzenia na potęgi liczb pierwszych 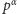 wygląda następująco:

Dla dowodu zauważmy, że po lewej stronie kongruencji mamy iloczyn wszystkich elementów grupy 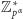 . Każdy element tej grupy ma zdefiniowany jednoznacznie element odwrotny. Iloczyn elementów, które nie są swoimi własnymi odwrotnościami, wynosi 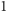 . Pozostaje zatem obliczyć iloczyn elementów spełniających równanie

Równanie to jest równoważne kongruencji 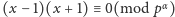, co dla 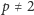jest równoważne 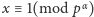lub 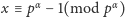. Zatem .

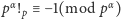W przypadku 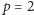mamy 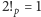, , 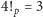a dla 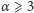równanie 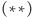 ma cztery rozwiązania: 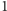,  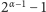, 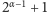i 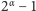 , których iloczyn modulo 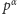 wynosi  .

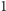Teraz już możemy pokazać, jak obliczać 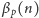 . Mianowicie, jeśli wprowadzimy oznaczenie 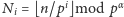, to

Dowód przeprowadzimy przez indukcję względem 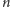 . Jeśli 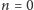, to wzór na 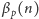 jest spełniony. Dla 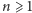załóżmy więc, że spełniony jest w przypadku 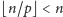i wywnioskujmy z tego prawdziwość dla 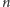 . Kluczową sprawą jest wyznaczenie 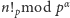. Każdą liczbę w tym iloczynie przedstawiamy w postaci 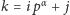, a następnie korzystamy z uogólnionego twierdzenia Wilsona:

W celu obliczenia 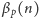 , liczby od 1 do  rozbijamy na dwie grupy: niepodzielne przez 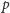 (ich iloczyn to oczywiście 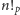 ) oraz resztę, do której zastosujemy założenie indukcyjne:

Dla ustalonego 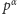 wartości 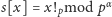dla 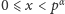możemy wyznaczyć w fazie obliczeń wstępnych. Faktycznie, 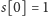oraz dla

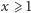
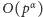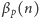zatem możemy to zrobić w czasie . Mając tablicę  , obliczamy  w czasie 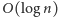. Ostatecznie, wzór 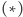obliczamy w czasie .

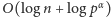Przejdźmy teraz do przypadku ogólnego. Chcąc obliczyć 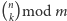, musimy najpierw rozłożyć moduł na iloczyn potęg liczb pierwszych

Możemy sobie pozwolić na zastosowanie naiwnego algorytmu 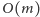 , gdyż i tak obliczanie tablic  zajmie czas .

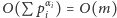Jeśli teraz oznaczymy 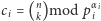, to z chińskiego twierdzenia o resztach dostajemy, że

gdzie 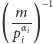oznacza odwrotność tego elementu w grupie 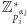 . Ponieważ

zatem obliczenie wszystkich odwrotności (również tych używanych przy obliczaniu 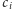 ) zabierze łączny czas 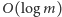. Ostatecznie obliczenie wartości 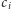 i wzoru 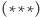 zajmie czas .

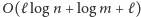Ponieważ 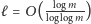, zatem ostatecznie dostajemy, że po wstępnych obliczeniach zajmujących czas 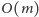 możemy obliczyć dowolny współczynnik dwumianowy 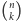modulo  w czasie .
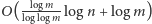