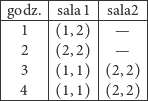
Dla przykładu załóżmy, że w szkole zatrudnionych jest dwóch nauczycieli, są dwie klasy oraz sześć przedmiotów: 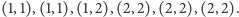Tutaj przedmioty opisujemy jako pary (numer nauczyciela, numer klasy). Zauważmy, że dany nauczyciel może wykładać danej klasie więcej niż jeden przedmiot.

Jeśli mamy do dyspozycji tylko jedną salę wykładową, to szkoła będzie musiała być otwarta przez 6 godzin (żadne zajęcia nie mogą odbywać się równolegle, a mamy ich sześć). Ale już dysponując dwiema salami, można skrócić ten czas do czterech godzin. Optymalny plan może wyglądać tak jak na rysunku obok.

Zadanie można sformułować w języku teorii grafów. Zbudujmy (multi)graf dwudzielny, którego wierzchołkami są nauczyciele i klasy, a krawędziami przedmioty (jeśli nauczyciel 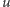ma uczyć klasę 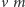przedmiotów, to mamy mkrawędzi łączących wierzchołki i w grafie). Stopniem wierzchołka nazwiemy liczbę krawędzi, które kończą się w tym wierzchołku. Ponadto przez 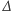oznaczymy maksymalny stopień wierzchołka w grafie (w naszym przykładzie ).

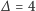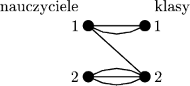
Niech 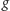będzie minimalną liczbą, dla której istnieje plan zajęć, który wymaga otwarcia szkoły na dokładnie 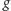godzin. Z treści zadania wynikają dwa oczywiste dolne ograniczenia na 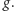Ponieważ żaden nauczyciel nie może prowadzić dwóch zajęć naraz ani żadna klasa nie może uczestniczyć w więcej niż jednych zajęciach naraz, więc 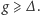Co więcej, jeśli mamy do dyspozycji s sal, to z zasady szufladkowej Dirichleta wynika, że 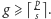Okazuje się, że są to jedyne ograniczenia i

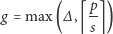
jest optymalnym rozwiązaniem zadania.

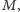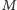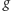Zanim to wykażemy, przypomnijmy kilka pojęć z teorii grafów. Skojarzeniem w grafie nazywamy taki podzbiór krawędzi że żadne dwie krawędzie z nie mają końca w tym samym wierzchołku. Kolorowaniem krawędziowym grafu na kolorów nazywamy rozkład zbioru krawędzi na sumę rozłącznych skojarzeń (część z nich może być pusta). Zatem, aby rozwiązać zadanie, musimy znaleźć rozkład grafu na rozłącznych skojarzeń, z których każde będzie zawierało co najwyżej krawędzi (krawędzie należące do danego skojarzenia reprezentują przedmioty, które będą prowadzone w tym samym czasie – ich przydział do sal jest dowolny).

Udowodnimy najpierw, że każdy graf dwudzielny można pokolorować na 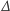 kolorów. W tym celu podamy algorytm, który będzie kolorował kolejne krawędzie grafu. Powiedzmy, że chcemy teraz pokolorować krawędź W wierzchołku u na pewno nie użyliśmy jeszcze wszystkich kolorów; powiedzmy, że został czerwony. Będziemy zatem chcieli pokolorować na czerwono. Jeśli w v nie użyliśmy czerwonego, to możemy to zrobić. W przeciwnym przypadku nie użyliśmy tam jakiegoś innego koloru (np. niebieskiego). Konstruujemy teraz w grafie ścieżkę 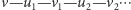, której krawędzie są na przemian czerwone i niebieskie. Szukamy przy tym ścieżki maksymalnej, tj. (jakiejkolwiek) takiej, której nie da się już przedłużyć. Ścieżka kiedyś się skończy (żaden wierzchołek nie może wystąpić na niej dwukrotnie, bo to by oznaczało, że pewne dwie krawędzie, które się w nim kończą, są obie czerwone albo obie niebieskie) i wtedy będziemy mogli zamienić kolory na tej ścieżce (niebieski na czerwony i na odwrót) i pomalować na czerwono. Zauważmy, że ścieżka nie mogła zawierać wierzchołka u, bo musiałaby wchodzić do niego niebieską krawędzią, zatem 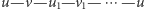byłoby cyklem nieparzystej długości, którego w grafie dwudzielnym być nie może.

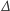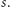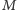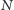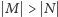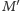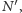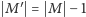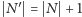Umiemy zatem rozłożyć graf na sumę  rozłącznych skojarzeń; niektóre z nich mogą jednakże mieć rozmiar większy niż Aby to naprawić, przyda nam się jeszcze jedna obserwacja: jeśli i są rozłącznymi skojarzeniami i , to istnieją rozłączne skojarzenia i takie że i oraz 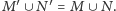Dowód tej obserwacji jest analogiczny jak dowód twierdzenia Berge’a o istnieniu ścieżki powiększającej względem skojarzenia, które nie jest najliczniejsze (można pokazać, że istnieje ścieżka długości nieparzystej, której krawędzie naprzemiennie należą do 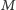i ) – 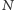opracowanie jego szczegółów pozostawiam Czytelnikowi.

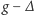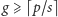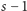Teraz do podziału dodajemy  pustych skojarzeń. Dopóki możemy znaleźć dwa skojarzenia, których moce różnią się o więcej niż 1, aplikujemy do nich powyższą obserwację. Ponieważ , to na końcu wszystkie skojarzenia będą miały rozmiar lub , czyli taki, jak trzeba.

Zauważmy na koniec, że zarówno kolorowanie grafu, jak i poprawianie kolorowania, można zrealizować w czasie