Ile mikroprocesorów jest w tym pokoju?
Maszyna Turinga
Maszyna Turinga (w skrócie MT) jest matematycznym modelem procesu obliczeniowego, wykonywanego przez wszystkie współczesne mikroprocesory. Dla zrozumienia zasady działania wystarczy nam następujący nieformalny opis. MT posługuje się nieskończoną taśmą podzieloną wzdłuż na równe pola. Pole może być puste lub zawierać jeden z symboli 0 lub 1. Tylko skończona liczba pól jest niepusta. Nad taśmą znajduje się głowica, która może czytać i modyfikować zawartość pól. Maszyna posiada skończoną liczbę stanów, w których może się znajdować. W każdym kroku po przeczytaniu zawartości pola maszyna, zależnie od swojego stanu, podejmuje decyzje: czy zmodyfikować zawartość tego pola, czy przesunąć głowicę w lewo, czy w prawo i jaki ma być nowy stan. Działanie maszyny można opisać za pomocą poniższej tabelki. Spójrzmy na przykład MT, która dodaje jedynkę do liczby zapisanej przy podstawie dwa.
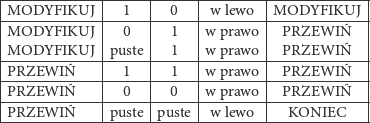
Aby wykonać obliczenie, na taśmie zapisujemy liczbę w postaci dwójkowej. Ustawiamy głowicę nad najmniej znaczącą cyfrą tej liczby i startujemy maszynę w stanie MODYFIKUJ. W tym stanie maszyna przegląda kolejne cyfry naszej liczby od najmniej znaczącej i zamienia kolejne napotkane 1 na 0. Pierwsze napotkane 0 lub puste pole zamienia na 1. Wówczas przechodzi do stanu PRZEWIŃ, w którym niczego nie modyfikuje, a tylko przesuwa głowicę z powrotem na pozycję początkową i kończy działanie. Przyjrzyjmy się przykładowi dla liczby 5. Strzałka oznacza położenie głowicy, a nazwa nad strzałką stan, w którym znajduje się maszyna.
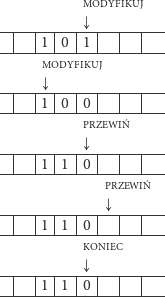
MT ze względu na prostotę dobrze nadaje się do matematycznego opisu procesu obliczeniowego. Można na niej zaprogramować każdy algorytm, ale jest to bardzo żmudne. Jako ćwiczenie proszę spróbować opisać maszynę dodającą dwie liczby.
Można też skonstruować (w myślach) Uniwersalną Maszynę Turinga (w skrócie UMT). Taka maszyna ma zakodowany algorytm symulowania dowolnej MT na podstawie jej opisu. Działa w ten sposób, że na taśmie zapisujemy, oprócz danych wejściowych, zakodowany za pomocą zer i jedynek opis aktualnie symulowanej maszyny. Innymi słowy jest to zakodowana tabelka opisująca tę maszynę. UMT jest pierwowzorem komputera. Jej tabelka funkcjonalnie odpowiada (mikro)procesorowi, a taśma pełni rolę pamięci.
Model von Neumanna
Wszystkie współczesne komputery działają w oparciu o Model von Neumanna.
W modelu tym mamy procesor oraz pamięć składającą się ze skończonej liczby
komórek. Każda komórka pamięta wartości ze skończonego zbioru
liczbowego. Można przyjąć, że są to liczby naturalne nie większe niż
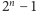 dla pewnego
dla pewnego
 , które interpretujemy jako liczbę bitów
pamiętanych w pojedynczej komórce. Komórki są ponumerowane liczbami
naturalnymi. Numery komórek nazywamy ich adresami. Część komórek
pamięci przeznaczona jest na przechowywanie danych, a część na
przechowywanie instrukcji wykonywanego programu. Podział jest dość
umowny – instrukcje też mogą być danymi, gdyż są zakodowane w postaci
liczb, aby mogły być przechowywane w pamięci. O tym, czy jakaś wartość
jest instrukcją czy daną, decyduje sposób jej użycia.
, które interpretujemy jako liczbę bitów
pamiętanych w pojedynczej komórce. Komórki są ponumerowane liczbami
naturalnymi. Numery komórek nazywamy ich adresami. Część komórek
pamięci przeznaczona jest na przechowywanie danych, a część na
przechowywanie instrukcji wykonywanego programu. Podział jest dość
umowny – instrukcje też mogą być danymi, gdyż są zakodowane w postaci
liczb, aby mogły być przechowywane w pamięci. O tym, czy jakaś wartość
jest instrukcją czy daną, decyduje sposób jej użycia.
Procesor pobiera instrukcje z pamięci i je wykonuje. Istnieje wyróżniona
komórka pamięci, zwana licznikiem programu, w której zapisany jest adres
komórki zawierającej aktualnie wykonywaną instrukcję. Potrzebujemy dwóch
rodzajów instrukcji. Pierwszy to instrukcje arytmetyczne. Taka instrukcja
mówi: jaką operację należy wykonać (dodawanie, odejmowanie itd.),
w których komórkach pamięci są argumenty tej operacji i gdzie ma
znaleźć się jej wynik. Po wykonaniu instrukcji arytmetycznej licznik
programu jest zwiększany o jeden i wskazuje na kolejną instrukcję do
wykonania. Drugi rodzaj to instrukcje sterujące. Umożliwiają one zmianę
licznika programu w sposób inny niż zwiększenie o jeden. Zmiana ta
może być warunkowa, uzależniona od wartości jakiejś komórki
pamięci. Przykładowo możemy mieć instrukcję, która mówi: jeśli
komórka pamięci o adresie
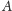 zawiera 0, to wpisz do licznika
programu wartość
zawiera 0, to wpisz do licznika
programu wartość
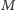 , a w przeciwnym przypadku zwiększ go
o jeden.
, a w przeciwnym przypadku zwiększ go
o jeden.
W naszym modelu niektóre komórki pamięci służą do komunikacji ze światem zewnętrznym. Możemy mieć komórki, w których pojawiają się kody liczbowe wciskanych klawiszy. Zawartość pewnych komórek może być interpretowana jako obraz, który ma być wyświetlany na monitorze.
Aby zacząć wykonywać program, zapisujemy go w pamięci. Następnie w odpowiednich komórkach umieszczamy dane. Ustawiamy licznik programu na wartość adresu pierwszej instrukcji programu i uruchamiamy maszynerię. Działa ona, dopóki jej nie wyłączymy, chyba że wcześniej wystąpi jakiś błąd w programie. Na tej właśnie zasadzie funkcjonują komputery.