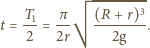Klub 44F - zadania X 2012»Zadanie 545
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44F - zadania X 2012
- Publikacja w Delcie: październik 2012
- Publikacja elektroniczna: 30 września 2012
- Artykuł źródłowy w wersji do druku [application/pdf]: (90 KB)
Satelita poruszający się po orbicie kołowej o promieniu
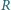 wokół planety
o promieniu
wokół planety
o promieniu
 został przyhamowany i zaczął poruszać się po orbicie
eliptycznej, stycznej do powierzchni planety. Wyznaczyć czas spadania satelity
na planetę. Przyspieszenie grawitacyjne na powierzchni planety wynosi
g.
został przyhamowany i zaczął poruszać się po orbicie
eliptycznej, stycznej do powierzchni planety. Wyznaczyć czas spadania satelity
na planetę. Przyspieszenie grawitacyjne na powierzchni planety wynosi
g.

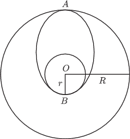
 orbity kołowej przedstawionej na rysunku. Ognisko elipsy, po której
zaczyna poruszać się satelita, znajduje się w punkcie
orbity kołowej przedstawionej na rysunku. Ognisko elipsy, po której
zaczyna poruszać się satelita, znajduje się w punkcie
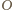 w środku
planety. Interesuje nas czas, po którym satelita znajdzie się w punkcie
w środku
planety. Interesuje nas czas, po którym satelita znajdzie się w punkcie
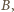 czyli połowa okresu obiegu po elipsie
czyli połowa okresu obiegu po elipsie
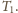 Z III prawa Keplera
mamy
Z III prawa Keplera
mamy
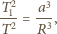
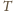 jest okresem obiegu satelity po orbicie kołowej, natomiast
jest okresem obiegu satelity po orbicie kołowej, natomiast
 – półosią wielką elipsy:
– półosią wielką elipsy:
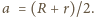 Okres obiegu po
orbicie kołowej wyznaczamy, wiedząc, że siła dośrodkowa jest siłą
grawitacji
Okres obiegu po
orbicie kołowej wyznaczamy, wiedząc, że siła dośrodkowa jest siłą
grawitacji
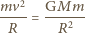
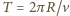 (
(
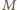 i
i
 to masy planety i satelity,
to masy planety i satelity,
 to prędkość satelity). Stąd
to prędkość satelity). Stąd
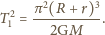
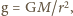 otrzymujemy szukany czas:
otrzymujemy szukany czas: