- Narzędzia
- Obiekty
- Słowa kluczowe
- Kategoria
- Mechanika
Klub 44F - zadania II 2012»Zadanie 532
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44F - zadania II 2012
- Publikacja w Delcie: luty 2012
- Publikacja elektroniczna: 1 lutego 2012
- Artykuł źródłowy w wersji do druku [application/pdf]: (65 KB)
Ciężarek o masie
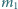 wisiał na sprężynce o stałej sprężystości
wisiał na sprężynce o stałej sprężystości
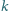 i drgał z amplitudą
i drgał z amplitudą
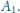 Z góry sypie się w tempie
Z góry sypie się w tempie
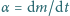 cienki strumień piasku, który spada ze stałą prędkością
cienki strumień piasku, który spada ze stałą prędkością
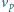 (stałą wskutek np. działania siły oporu powietrza). Piasek pada
na ciężarek i przykleja się, dalej drgając razem z nim. Po czasie długim
w porównaniu z okresem drgań masa ciężarka wraz z piaskiem wzrosła do
wartości
(stałą wskutek np. działania siły oporu powietrza). Piasek pada
na ciężarek i przykleja się, dalej drgając razem z nim. Po czasie długim
w porównaniu z okresem drgań masa ciężarka wraz z piaskiem wzrosła do
wartości
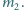 Znaleźć końcową amplitudę drgań. Założyć, że
prędkość ruchu ciężarka nie przekraczała prędkości spadku piasku.
Znaleźć końcową amplitudę drgań. Założyć, że
prędkość ruchu ciężarka nie przekraczała prędkości spadku piasku.
Rozwiązanie
Przyjmijmy, że ciężarek porusza się z prędkością
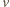 do góry, wtedy
jego prędkość względem piasku wynosi
do góry, wtedy
jego prędkość względem piasku wynosi
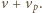 Ponieważ masa piasku
na jednostkę długości strumienia jest równa
Ponieważ masa piasku
na jednostkę długości strumienia jest równa
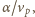 więc masa piasku
przyklejonego w ciągu czasu
więc masa piasku
przyklejonego w ciągu czasu
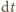 wynosi
wynosi
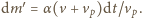 Energia
przekształcona w ciepło jest równa
Energia
przekształcona w ciepło jest równa
W ciągu jednego okresu masa ciężarka nie zmienia się znacząco
i można przyjąć, że jego ruch jest w przybliżeniu harmoniczny:
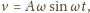 gdzie
gdzie
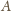 jest amplitudą,
jest amplitudą,
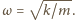 Gdy
podstawimy zależność
Gdy
podstawimy zależność
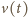 do
do
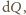 rozwiniemy sześcian
i scałkujemy względem okresu, niezerowy wkład do całki dadzą tylko parzyste
potęgi
rozwiniemy sześcian
i scałkujemy względem okresu, niezerowy wkład do całki dadzą tylko parzyste
potęgi
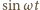 – zerowa i druga:
– zerowa i druga:
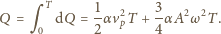
Pierwszy składnik po prawej stronie jest początkową energią kinetyczną piasku
przyklejonego w ciągu okresu, zatem drugi składnik
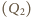 jest spadkiem
energii drgań w tym czasie. Przechodząc do dłuższej skali czasu, należy
wyrażenie
jest spadkiem
energii drgań w tym czasie. Przechodząc do dłuższej skali czasu, należy
wyrażenie
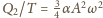 przyrównać do
przyrównać do
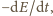 gdzie
gdzie
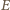 jest energią drgań ciężarka,
jest energią drgań ciężarka,
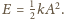 Stąd
Stąd
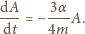
Podstawienie
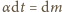 i scałkowanie prowadzi do wyniku
i scałkowanie prowadzi do wyniku
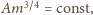 czyli
czyli
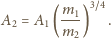
Jak widać, wartość prędkości piasku nie ma znaczenia.
