Sprawy zmieniają się istotnie, gdy od zwykłych dla nas zjawisk makroświata przejdziemy do skali atomowej czy mniejszej. Teorią konieczną do opisu zjawisk w takiej skali jest mechanika kwantowa. Inaczej niż przywykliśmy, teoria ta obejmuje kwestie formalne, a opis pomiaru (w kategoriach bardzo ogólnych) jest jej istotną częścią. Zjawiska fizyczne przestają być obojętne na to, czy je obserwujemy, czy nie. Żeby pokazać różnicę przynajmniej na poziomie zasad, zastąpię garnek z wodą zmyślonym garnkiem ze zmyśloną wodą, który udawać będzie system podległy mechanice kwantowej. Przełożenie tej teorii na praktykę omówimy pobieżnie później. Wiadomo, że zanim woda się zagotuje, musi przejść przez stan pośredni, kiedy "bąbelkuje". Zmyślona woda rządzić się będzie takim przewrotnym prawem: ilekroć podnosimy przykrywkę, nigdy nie widzimy, by "bąbelkowała". Może nie wrzeć lub może wrzeć, póki trzymamy podniesioną przykrywkę, ale nic innego. Lecz nie może zacząć wrzeć, jeśli wcześniej nie zaczęła bąbelkować, a stąd wniosek, że nigdy nie zacznie wrzeć, gdy będziemy trzymać podniesioną przykrywkę.

Opuśćmy zatem przykrywkę na czas 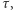po czym ją podnieśmy. Jak będzie zachowywać się woda udająca system kwantowy? Okazuje się, że probabilistycznie: dla danego czasu woda po odsłonięciu będzie wrzeć z prawdopodobieństwem 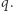Spróbujmy zatem zagotować wodę w czasie 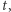sprawdzając w tym czasie razy co czas 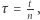czy nam się udało (zakładamy, że podnosimy przykrywkę na zaniedbywalnie krótki moment). Prawdopodobieństwo, że w czasie 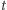nie uda nam się zagotować wody, wynosi

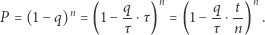Zapisaliśmy to tak, by przypominało definicję liczby Eulera :

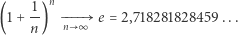Łatwo z tej definicji wykazać (zastępując przez 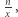gdzie 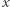jest stałe), że

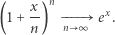Gdy 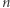jest duże, fizycy na ogół nie przejmują się, że nie jest nieskończone. Zatem zapiszmy prawdopodobieństwo niezagotowania wody jako zależność wykładniczą

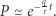Nasze szanse zagotowania wody zależą zatem od tego, jak 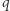zależy od 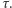Kolejną rzecz, którą zwykli robić fizycy, jest rozwijanie funkcji w szereg potęgowy: 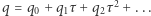i zaniedbywanie wyższych potęg, jeśli 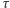jest małe (a takie jest, bo mamy zamiar często sprawdzać, czy woda już się zagotowała). Ponieważ powiedzieliśmy, że woda nie może zacząć wrzeć, póki nie zacznie "bąbelkować", należy przyjąć, że 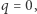gdy 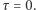Musi zatem być 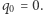Okazuje się też, że musi zachodzić 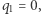by nasz garnek z wodą poprawnie udawał system kwantowy. Zatem najniższy nieznikający parametr w rozwinięciu 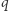występuje przy drugiej potędze 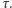Możemy więc przybliżyć:

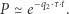Im częściej sprawdzamy wodę, tym mniejsze jest 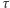i tym mniejsza jest wartość absolutna wykładnika w powyższym wzorze. W konsekwencji 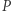spada wolniej, czyli większe jest prawdopodobieństwo, że będziemy dłużej czekać na zagotowanie. Cały zaś proces zatrzymałby się zupełnie przy 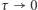(w tej granicy uzyskujemy, jak widać, ten sam wynik, co w przypadku, gdy trzymamy pokrywkę cały czas podniesioną).

Podsumujmy. Zmyślony garnek udaje system kwantowy, stosując się do trzech regułek: (1) nigdy nie daje się zaobserwować w stanie pośrednim; (2) gdy jest obserwowany, zachowuje się probabilistycznie; (3) dla krótkich czasów przebywania w stanie pośrednim prawdopodobieństwa są w przybliżeniu proporcjonalne do kwadratu tego czasu (zerowy i pierwszy wyraz rozwinięcia znika). Zwróćmy też uwagę na założenie implicite, że podnoszenie i opuszczanie przykrywki udaje procedurę pomiarową na systemie kwantowym. Skutkiem stosowania tych regułek jest to, że im częściej sprawdzamy, co się dzieje, tym z mniejszym prawdopodobieństwem zobaczymy jakąkolwiek zmianę. Zjawisko to jest rzeczywiste dla systemów mikroskopowych; z rzadka tylko nazywane jest efektem pilnowanego garnka ( "a watched pot effect"), a dużo szerzej znane jest pod mianem kwantowego efektu Zenona. Drugi tytuł zawdzięczamy skojarzeniu z poglądami starożytnego greckiego filozofa Zenona z Elei. Dowodził on niemożności ruchu (i w konsekwencji jakiejkolwiek zmiany) poprzez myślowe rozbieranie rzeczywistych ruchów na coraz drobniejsze fragmenty. Zgodnie z regułą, że jeśli rzeczywistość nie zgadza się z teorią, to tym gorzej dla rzeczywistości - Zenon twierdził, że zmysły nas mamią. Być może zgodziłby się on na kompromis, jaki wynika z powyższych rozważań: świat zmienia się, gdy przymykamy na to oko.

Omówimy teraz, na ile zastosowane regułki symulują rzeczywistość.

(1) Zmyślony garnek symuluje nam "prosty" układ mikroskopowy. Może to być np. niestabilne jądro atomowe, atom z jednym elektronem na wyższym poziomie energetycznym lub atom uwięziony w pułapce optycznej, tzn. w potencjale wytworzonym przez przecinające się wiązki laserowe. Czytelnik słusznie zaprotestuje przeciw nazwaniu dowolnego z tych układów prostym. Prostota takiego układu ma polegać na tym, że może on znajdować się tylko w jednym z dwóch stanów. Stan 1: woda się nie gotuje, jądro się nie rozpadło, elektron wciąż znajduje się w stanie wzbudzonym, a atom wewnątrz pułapki. Stan 2: woda wrze, jądro się rozpadło, elektron opadł na niższy poziom, emitując foton, a atom uciekł z pułapki.

Nie obserwujemy jądra, które już-już zaczyna pękać. Elektron przechodząc od jednego poziomu do drugiego, oddaje energię w postaci dokładnie jednego fotonu - kwantu światła. Nie obserwujemy nigdy, by elektron stopniowo wypuszczał strużkę energii w trakcie zmieniania poziomu. Podobnie jednoznacznie zachowuje się też atom w pułapce optycznej - albo jest w pułapce, albo poza nią. Zaznaczmy, że do pomyślenia jest sytuacja, gdy układ przechodziłby przez jakieś obserwowalne stany pośrednie, np. jądro miałoby jakiś dodatkowy stan wzbudzony, a elektron przed przejściem do najniższego poziomu energetycznego mógłby się znaleźć w jakimś pośrednim, emitując w sumie dwa fotony po drodze. Kwantowość jednak polega tu na nieciągłości: mamy konkretne stany, które da się zaobserwować, i nic pośredniego między nimi. Układ z większą liczbą stanów działać będzie na tej samej zasadzie co układ z dwoma.

(2) Kwintesencją kłopotów z pomiarami w mechanice kwantowej jest rozsławiona szeroko po świecie zasada nieoznaczoności Heisenberga. Wedle niej, gdy mierzymy położenie jakiejś swobodnie poruszającej się cząstki, to nigdy nie znamy jej pędu, i odwrotnie: gdy zmierzymy pęd, nie znamy położenia. Możemy próbować mierzyć i pęd, i położenie, ale otrzymany wynik jest zawsze obarczony niepewnością. Im jedno znamy dokładniej, tym drugie mniej, i to z fizycznej konieczności, a nie z powodu niedoskonałości naszych pomiarów. Oznacza to, że gdy nie mierzymy ani położenia, ani pędu, to cząstka znajduje się w stanie, dla którego nie jest określone ani konkretne położenie, ani konkretny pęd. Stan układu jest tak zwaną superpozycją stanów o różnych położeniach i różnych pędach. Skoro pomiary pędu i położenia mają wbudowaną niedokładność, to znaczy, że rządzi nimi prawo probabilistyczne; konkretne prawdopodobieństwa zmierzenia takiego czy innego pędu lub położenia zadane są przez wewnętrzne parametry tej superpozycji (czyli, inaczej mówiąc, funkcję falową).

W podobnej (acz prostszej) sytuacji jest nasz "prosty" układ kwantowy - jeśli nie jest obserwowany, to jest w superpozycji stanu 1 i stanu 2. W moim zmyślonym modelu gotującej się wody rolę superpozycji pełniła woda "bąbelkująca", czyli taka w stanie pośrednim. Jak widać może z poprzedniego akapitu, nazwanie superpozycji jedynie stanem pośrednim między dwoma stanami możliwymi do zaobserwowania jest pewnym zubożeniem. Superpozycja aspiruje raczej do bycia jedynym właściwym opisem fizycznego stanu. My jednak chcieliśmy co chwila nasz system sprawdzać, sprowadzając superpozycję do stanu 1 lub 2, stąd takie porównanie. Superpozycji, dodam, nie można traktować jako zwykłego rozkładu prawdopodobieństwa różnych stanów, o czym z braku miejsca wspominam bez podania uzasadnienia.

(3) Dla długich czasów prawdopodobieństwo pozostania w stanie początkowym (przy braku pomiaru) w powyższych przykładach zanika wykładniczo. Jest to rezultat tzw. Złotej Reguły Fermiego. Można łatwo sprawdzić, że w takim przypadku (kiedy 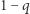zanika wykładniczo) ścisły wynik modelu z garnkiem nie przejawiałby zależności od 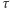ani nawet nie różniłby się od sytuacji bez pomiaru. Lecz dla krótkich czasów zachodzi odejście od zaniku wykładniczego. W szczególności dla dostatecznie krótkich czasów, jak wspomniałem, owo prawdopodobieństwo zanika kwadratowo. Jest to prawdą dla każdego systemu kwantowego. Dla różnych układów i częstotliwości pomiarów możemy mieć różne efekty; z reguły dla małej częstotliwości spodziewamy się obowiązywania Złotej Reguły, a dla dużej - kwantowego efektu Zenona. Zdarzają się jednak układy z zakresami częstotliwości, w których zachodzi efekt anty-Zenona: przyspieszenie zmian wskutek obserwacji. Jest to coś, na co Zenon z Elei za żadne skarby by się nie zgodził.

Zostało nam zatem do omówienia założenie o podnoszeniu przykrywki garnka i, jak to zwykle bywa z założeniami implicite, jest ono najbardziej kłopotliwe. Z podanych przykładów właściwie tylko w przypadku atomów uciekających z pułapki optycznej można zrealizować bez większych problemów (i zrealizowano) scenariusz przypominający nasze zmyślone gotowanie wody. Inne doświadczenia badające efekt Zenona zwykle wykorzystują silne pulsy laserowe przy pomiarach. Choć z punktu widzenia teorii przedstawiona analogia garnka jest wciąż akceptowalna, taki pomiar mało przypomina subtelne zaglądanie pod lekko podniesioną przykrywkę.

Zresztą, wzorem Zenona, zaskakujący rezultat braku zmian przy ciągłej obserwacji winien nas naprowadzić na trop, że coś jest nie tak. Inaczej niż Zenon podejrzewać winniśmy raczej teorię - opis pomiaru należy poprawić. Potrzebny jest opis kwantowy nie tylko mierzonego układu, ale też i aparatury pomiarowej, na szczęście traktowanej wciąż w bardzo uproszczony sposób. Lecz oddziaływanie jednego z drugim, nawet niebezpośrednie (np. detektor rejestrujący foton wyemitowany przez elektron zmieniający stan energetyczny) wciąż może wywoływać efekt Zenona lub anty-Zenona, przynajmniej w teorii. Nie może jednak zupełnie zatrzymać układu mierzonego, jak mogło się zdarzyć w stosowanym tu modelu. Czy Zenon z Elei by się na to zgodził? Być może twierdziłby, że mamią nas detektory, jeśli nie zmysły...