Komputery kwantowe (KK) okazują się łączyć oba aspekty plecenia. Patrząc z tej drugiej strony, specjaliści obiecują wiele, albo i więcej, ale dopiero (albo "i to już") jutro [1]. Nie wiadomo jednak, z czego KK miałby być ostatecznie wyrzeźbiony.

Podejścia są w zasadzie trzy, choć kryteria tego podziału nie są jednolite. Parafrazując, można powiedzieć, że KK może być np. zielony, kwadratowy lub konopny.

Jeden odłam to podejście "analogowo-kwantowe", które już jest wykorzystywane praktycznie np. przez D-Wave (patrz str. 12). Drugie to dążenie do wykazania tzw. przewagi kwantowej [2] za pomocą relatywnie małych macierzy kubitów (np. 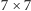). Układy te mają, w zasadzie, działać według standardowego modelu obliczeń kwantowych. To, czego im będzie brakować, to korekcja błędów, która wymaga nadmiarowej liczby kubitów. Google twierdzi, że to już znajdzie zastosowanie praktyczne czy wręcz komercyjne, a usługę chce świadczyć poprzez chmurę [3]. W tym podejściu sprawą nadal otwartą jest technologia tworzenia kubitów (Google ma konkurentów).

O ostatnim podejściu jeszcze w tym numerze Delty nie pisaliśmy. Chodzi o tytułowe wyplatanie, czyli topologiczny komputer kwantowy. Jest to coś, co ma szansę rozwiązać wszystkie problemy, tylko na razie nie wiadomo, czy to, z czego ma zostać wypleciony, w ogóle istnieje, albo czy to, co wygląda na istniejące, jest tym, czym się być wydaje.

Za ojca chrzestnego tego nurtu można uznać Kitajewa [4], który właśnie za to został pięć lat temu jednym z pierwszych laureatów Fundamental Physics Prize, o czym pisaliśmy w Delcie 2/2013. Chodzi o jeden ze sposobów wykorzystania topologicznych stanów materii (TSM), za odkrycie których przyznano zeszłoroczną Nagrodę Nobla z Fizyki.

Nibymateriałem potrzebnym do tej plecionki mają być anyony i to koniecznie w postaci nieabelowego TSM, a najlepszym kandydatem na te nibycząstki (pseudocząstki, kwazicząstki) wydają się być fermiony Majorany.

O co dokładnie chodzi, nie napiszę. Mógłbym zasugerować, że nie ma tu wystarczająco dużo miejsca, ale powód jest dużo prostszy - nie czuję się kompetentny. Polecam natomiast opracowanie [5], przynajmniej jeżeli chodzi o sam anyonowy TSM. Można też zapoznać się z amerykańskim patentem [6].

Anyony to kolektywne ekscytacje w materii o obniżonej liczbie wymiarów. W trójwymiarze identyczne (niby)cząstki mogą być albo fermi-onami, albo bos-onami, dla których podwójna zamiana cząstek jest operacją albo antysymetryczną (faza 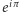), albo symetryczną 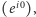bo linie świata cząstek nie zapętlają się - w przeciwieństwie do sytuacji w dwóch wymiarach. Dlatego faza może być tam dowolna 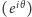i stąd nazwa: any-on. Zaplatanie anyonów jest opisywane za pomocą (nieabelowej) grupy warkoczowej zamiast uboższej grupy permutacji.

Fermiony Majorany, o które w kontekście KK budowanego z TSM chodzi, to nibycząstki będące połączeniem połowy elektronu z połową dziury. Nie mają ładunku, nie mają masy, są swoimi własnymi antycząstkami i występują parami. Powinny się pojawiać w jednowymiarowych nadprzewodnikach z polem magnetycznym skierowanym wzdłuż nich. Przewidziało to prawie jednocześnie kilka grup teoretycznych w 2010 roku, a pierwsze potwierdzenie uzyskano dwa lata później [7]. Niedawno (innymi metodami) otrzymano wyniki [8-10] na tyle wyraźne, że idea budowy KK z fermionów Majorany wydaje się być w zasięgu ręki (optymistom, którzy przy okazji obiecują międzymordzie w Visual Studio [11]). Wymyślenie, dlaczego nibycząstki pojawiające się w jednowymiarowych materiałach też mogą być anyonami, warte było części zeszłorocznej Nagrody Nobla z Fizyki.

Ich fantastyczną cechą (z punktu widzenia budowy KK) jest to, że żyją na dwóch końcach nanodrutu z nadprzewodnika. Ta ich "topologiczność" powoduje, że są niewrażliwe na zakłócenia, które nieuchronnie prowadziłyby do dekoherencji zbudowanego z nich kubitu. W ten sposób podstawowe ograniczenie związane z rzeźbieniem kubitów znika przy ich pleceniu (według optymistów).

Sytuacja jednak jest taka, że na razie mamy coś, co być może jest włóczką, a już sprzedają nam arras. Głównym sponsorem rozproszonego warsztatu tkackiego jest Microsoft. Środków raczej nie zabraknie, ale czy międzymordzie będzie działać, to ja nie wiem.