Skąd się bierze długość Plancka?
Już około 2500 lat temu Leukip i Demokryt z Abdery wiedzą, że świat składa się wyłącznie z niepodzielnych elementów materii ("atomów") oraz z próżni. Mechanika Newtona (XVII w.) operująca pojęciami absolutnego czasu i absolutnej przestrzeni umożliwia po raz pierwszy w historii jakościowy opis zachowania się cząstek materii (np. planet, a także fotonów uznawanych wówczas za korpuskuły). Faraday i Maxwell (XIX w.) dodają do listy składników świata pojęcie pola (np. pole elektromagnetyczne). Teoria względności Einsteina (XX w.) łączy czas i przestrzeń: dzięki temu na początku minionego stulecia świat składa się z czasoprzestrzeni, cząstek i pól, przy czym pole grawitacyjne zostało powiązane z nieeuklidesową geometrią czasoprzestrzeni...
Przełomy związane z mechaniką kwantową (Planck, Bohr, Born, Jordan, Heisenberg, Dirac, Feynman...) doprowadzają do kolejnej unifikacji: cząstki są w istocie konsekwencją istnienia pól (kwantami pól)... W połowie XX wieku do opisu świata potrzeba więc jedynie kwantowych pól oraz czasoprzestrzeni. Aktualnym wyzwaniem jest zrozumienie, w jaki sposób skwantować pole grawitacyjne: dotychczas było ono bowiem zawsze opisywane przy użyciu klasycznej, choć krzywoliniowej, geometrii. Jeśli grawitacja jest kwantowa, powinien istnieć charakterystyczny, minimalny rozmiar kwantu przestrzeni, przy którym czasoprzestrzeń przestaje wydawać się ciągła.
Zanim oszacujemy ten rozmiar, przypomnijmy naturalne jednostki miary zaproponowane przez Maksa Plancka w 1899 roku:
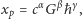 |
gdzie  oznacza prędkość światła,
oznacza prędkość światła, 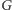 stałą grawitacji Newtona, a
stałą grawitacji Newtona, a 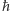 zredukowaną stałą Plancka (
zredukowaną stałą Plancka ( 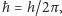 gdzie
gdzie 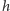 to stała Plancka). Dobierając odpowiednie potęgi
to stała Plancka). Dobierając odpowiednie potęgi 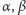 i
i 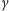 można dostać charakterystyczną długość
można dostać charakterystyczną długość 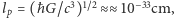 masę
masę 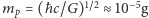 oraz czas
oraz czas 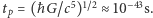
Wraz ze sformułowaniem zasady nieoznaczoności Heisenberga, 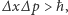 określającej pary wielkości (np. położenie
określającej pary wielkości (np. położenie  i pęd
i pęd 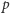 ), których nie da się zmierzyć jednocześnie z dowolną dokładnością, pojawiło się pytanie, czy w związku z tym nieoznaczoność przeszkadza przy pomiarze składowych jakiegoś interesującego nas kwantowego pola. W 1933 roku Bohr i Rosenfeld dostarczyli odpowiedzi dla pola elektromagnetycznego: mimo kwantowej nieoznaczoności można mierzyć składowe tego pola z dowolną dokładnością. Czy podobnie jest dla pola grawitacyjnego? Problem polega na tym, że w przeciwieństwie do przypadków kwantowych pól znajdujących się w czasoprzestrzeni, w której dokonujemy pomiaru, pole grawitacyjne jest czasoprzestrzenią.
), których nie da się zmierzyć jednocześnie z dowolną dokładnością, pojawiło się pytanie, czy w związku z tym nieoznaczoność przeszkadza przy pomiarze składowych jakiegoś interesującego nas kwantowego pola. W 1933 roku Bohr i Rosenfeld dostarczyli odpowiedzi dla pola elektromagnetycznego: mimo kwantowej nieoznaczoności można mierzyć składowe tego pola z dowolną dokładnością. Czy podobnie jest dla pola grawitacyjnego? Problem polega na tym, że w przeciwieństwie do przypadków kwantowych pól znajdujących się w czasoprzestrzeni, w której dokonujemy pomiaru, pole grawitacyjne jest czasoprzestrzenią.
W praktyce pomiar oznacza detekcję oddziaływania pola z jakąś materialną cząstką, która znajduje się w położeniu 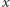 z określoną dokładnością
z określoną dokładnością 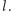 Stosując zasadę Heisenberga nieoznaczoność położenia musi spełniać nierówność
Stosując zasadę Heisenberga nieoznaczoność położenia musi spełniać nierówność 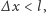 czyli
czyli 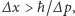 a więc
a więc 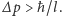 Dla dużych wartości pędu średnia wartość kwadratu pędu
Dla dużych wartości pędu średnia wartość kwadratu pędu 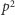 jest większa od
jest większa od 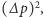 co daje oszacowanie
co daje oszacowanie 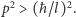 Wynik ten jest oczywistą konsekwencją zasady nieoznaczoności: duża dokładność pomiaru położenia wymaga dużych pędów. Z tego powodu w doświadczeniach akceleratorowych, w których bada się coraz mniejsze skale odległości, zderzają się bardzo szybkie cząstki. Energia relatywistycznej cząstki o masie spoczynkowej
Wynik ten jest oczywistą konsekwencją zasady nieoznaczoności: duża dokładność pomiaru położenia wymaga dużych pędów. Z tego powodu w doświadczeniach akceleratorowych, w których bada się coraz mniejsze skale odległości, zderzają się bardzo szybkie cząstki. Energia relatywistycznej cząstki o masie spoczynkowej 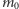 i pędzie
i pędzie 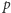 to
to 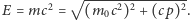 Dla dużych pędów energia związana z masą spoczynkową
Dla dużych pędów energia związana z masą spoczynkową 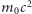 jest zaniedbywalna, więc można przyjąć, że
jest zaniedbywalna, więc można przyjąć, że 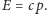 Dokładny pomiar położenia wymaga zatem jak największej energii w jak najmniejszej objętości.
Dokładny pomiar położenia wymaga zatem jak największej energii w jak najmniejszej objętości.

Jak dużo energii można zgromadzić w jednym miejscu? W teorii względności energia jest równoważna masie 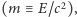 więc podobnie do "zwykłej" masy zakrzywia przestrzeń wokół miejsca, w którym jest zlokalizowana. Interesującym nas ograniczeniem na ilość masy-energii jest krytyczne zakrzywienie, przy którym powstaje czarna dziura. Rozmiar czarnej dziury (promień Schwarzschilda) to
więc podobnie do "zwykłej" masy zakrzywia przestrzeń wokół miejsca, w którym jest zlokalizowana. Interesującym nas ograniczeniem na ilość masy-energii jest krytyczne zakrzywienie, przy którym powstaje czarna dziura. Rozmiar czarnej dziury (promień Schwarzschilda) to 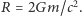 Zmniejszanie
Zmniejszanie 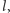 czyli coraz bardziej precyzyjna lokalizacja, prowadzi do, jak nakazuje zasada nieoznaczoności, zwiększania masy-energii, jednak jedynie do momentu, w którym
czyli coraz bardziej precyzyjna lokalizacja, prowadzi do, jak nakazuje zasada nieoznaczoności, zwiększania masy-energii, jednak jedynie do momentu, w którym 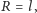 ponieważ dla
ponieważ dla 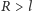 nasz system pomiarowy zaczyna znajdować się wewnątrz czarnej dziury, do której z definicji nie mamy dostępu. Łącząc powyższe oszacowania, otrzymujemy minimalny rozmiar wyznaczony przez prawa fizyki:
nasz system pomiarowy zaczyna znajdować się wewnątrz czarnej dziury, do której z definicji nie mamy dostępu. Łącząc powyższe oszacowania, otrzymujemy minimalny rozmiar wyznaczony przez prawa fizyki:
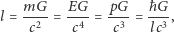 |
czyli
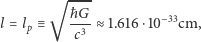 |
a więc (niespodzianka!) minimalnym rozmiarem okazuje się długość Plancka 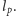 Mimo, że przedstawione argumenty opierają się w zasadzie o klasyczną fizykę, ich znaczenie jest jasne: dla odległości porównywalnych z
Mimo, że przedstawione argumenty opierają się w zasadzie o klasyczną fizykę, ich znaczenie jest jasne: dla odległości porównywalnych z 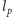 czasoprzestrzeni nie można już uważać za ciągłą, a dla długości mniejszych od
czasoprzestrzeni nie można już uważać za ciągłą, a dla długości mniejszych od 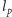 pojęcie odległości w ogóle traci sens.
pojęcie odległości w ogóle traci sens.
Ziarnistość czasoprzestrzeni w najmniejszych skalach prowokuje pytania o możliwe odstępstwa od uznanych klasycznych teorii (np. czy istnienie minimalnego rozmiaru wymaga modyfikacji szczególnej teorii względności?), ale z drugiej strony rozwiązuje paradoks Zenona z Elei, o którym na pewno wiedział Demokryt: na skwantowanej bieżni Achilles zawsze dogoni żółwia.