Klasycznie cząstka ma w każdej chwili położenie i prędkość (bądź skoligacony z nią pęd), co oznacza, że jej własności są określone i istnieją realnie, bez względu na to, czy ktoś lub coś je mierzy. W opisie kwantowym wielkości te nie są określone, dopóki obserwator nie dokona ich pomiaru. Przed pomiarem cząstce przypisuje się całą gamę możliwych położeń czy pędów. Ta wielość współistniejących możliwości zawarta jest w stanie kwantowym.

By wyrobić sobie pewną intuicję dotyczącą tego, czym jest ten obiekt, przypomnijmy, że fundamentem fizyki klasycznej jest równanie Newtona, które wiąże zmianę pędu układu z działającymi nań siłami. Rozwiązanie tego równania to podanie pędu i położenia cząstki w każdej chwili. Każda z tych wielkości jest wektorem w przestrzeni trójwymiarowej, zatem ruch cząstki, czyli jej trajektoria, rozumiana jako podanie pary pęd + położenie, będzie krzywą w przestrzeni o sześciu wymiarach. Cząstce kwantowej nie można przypisać pojedynczej krzywej, co oznacza, że nie ma ona dokładnie określonego pędu bądź położenia. Po przejściu do świata kwantów klasyczna trajektoria rozmywa się na cały zbiór możliwości zawartych w stanie kwantowym, którego ewolucję wyznacza równanie Schrödingera.

W ramach teorii kwantów cząstka opisywana jest w taki sposób, jakby była właśnie rozmyta, czyli znajdowała się w wielu konfiguracjach fizycznych naraz, zaś zjawisko to nazywamy superpozycją. W ramach powszechnie stosowanej interpretacji mechaniki kwantowej, zwanej "kopenhaską", dopiero akt pomiaru danej wielkości fizycznej - na przykład położenia albo pędu - określa jej wartość, pozostawiając pozostałe w ogólności nieznane. Interpretacja ta stawia obserwatora, poprzez dokonywany przezeń pomiar, na wyróżnionej pozycji, jako urządzenia bądź istoty nadającej układowi fizycznemu określone cechy. Probabilistyczna natura teorii kwantów objawia się w tym, że nie można powiedzieć, która z wielu możliwości zawartych w stanie kwantowym stanie się realnym bytem na skutek pomiaru. Można jedynie powiedzieć, z jakim prawdopodobieństwem - określonym poprzez dynamikę stanu kwantowego zgodnie z równaniem Schrödingera - obserwator zarejestruje dany wynik.

Konsekwencje opisu układu fizycznego poprzez stan kwantowy są wielorakie. Einstein, Podolsky i Rosen pokazali, że dwie cząstki można przygotować w pewnym stanie superpozycji, oddalić wzajemnie na znaczną odległość, a następnie zmierzyć, na przykład, położenie jednej z nich, co nieskończenie szybko określa położenie drugiej[1]. Wydawać by się mogło, że prowadzi to do natychmiastowej komunikacji, w szczególności szybszej, niż pozwala na to ograniczenie, jakie nakłada prędkość światła. Spostrzeżenie to sprowokowało Einsteina od ukucia frazy o "upiornym działaniu na odległość", i było dla niego kolejnym argumentem na rzecz niesłuszności bądź niepełności opisu kwantowego. Nieomal trzydzieści lat później John Bell opublikował pracę, w której dowiódł, że powyższe zjawisko, prowadzące do tak zwanego paradoksu EPR, jest przejawem nielokalności mechaniki kwantowej [2]: dwie cząstki, mimo że odległe, nie stanowią osobnych bytów, dopóki nie dokona się na nich pomiaru. Przed pomiarem stanowią jeden układ, mimo że nie są w żaden sposób mechanicznie powiązane. W układach, w których jest wiele cząstek, superpozycja może prowadzić do szczególnej między nimi relacji, nazywanej splątaniem. Przykładem wielocząstkowego stanu splątanego jest sławny kot Schrödingera, który "będąc naraz" martwy i żywy, dopiero dzięki obserwatorowi wytrąca się z tej upiornej superpozycji. Splątanie jest zasobem - pozwala na osiąganie niezwykłej dokładności pomiarów [3, 4], na przykład poprzez planowaną poprawę czułości detektorów fal grawitacyjnych [5, 6, 7].

Na wczesnym etapie rozwoju teorii kwantów dostrzeżono, że opis cząstki poprzez stan kwantowy niesie pewną szczególną konsekwencję, zwaną obecnie zasadą nieoznaczoności Heisenberga. Można ją sformułować na wiele sposobów, my przytoczymy ten, który jest powszechnie uznany i nie budzi kontrowersji: zasada nieoznaczoności Heisenberga mówi, że nie można przygotować cząstki w takim stanie kwantowym, by zarówno jej położenie, jak i pęd były określone.

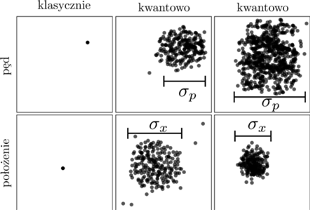
Rozkład położeń i pędów mierzonych dla cząstki opisywanej równaniem Newtona (lewa kolumna) oraz Schrödingera (środkowa i prawa kolumna). Klasycznie wyniki pomiarów przeprowadzonych w identycznych warunkach nie różnią się. Kwantowo zarówno położenie, jak i pęd mają rozrzuty, których wartości połączone są zasadą nieoznaczoności Heisenberga. Przygotowanie cząstki w stanie, który ma mały rozrzut położeń, skutkuje większym rozrzutem pędów.

By zrozumieć wagę tego twierdzenia, przeprowadźmy następujący eksperyment myślowy. Rozważmy działko, które w regularnych odstępach czasu wystrzeliwuje w identyczny sposób pojedyncze elektrony. Po wystrzeleniu pozwalamy elektronowi lecieć przez pewien czas (za każdym razem ten sam), po czym mierzymy jego położenie. Powtarzamy doświadczenie miliony razy, zawsze notując, gdzie elektron został zaobserwowany. Gdyby nie prawidła mechaniki kwantowej, elektron zawsze dolatywałby do tego samego punktu (oczywiście zakładając, że przebieg całego doświadczenia zawsze jest ten sam). Dzieje się tak dlatego, że równanie Newtona daje jednoznaczny związek końcowego położenia cząstki z działającymi nań siłami i warunkami początkowymi. Lecz elektronem rządzi teoria kwantów, co sprawia, że mierzone położenia będą miały pewien rozrzut, który oznaczmy przez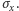

W następnym kroku powtarzamy doświadczenie kolejne miliony razy, mierząc, zamiast położenia, pęd cząstki. Znów w ramach mechaniki newtonowskiej należałoby się spodziewać za każdym razem tego samego wyniku. W rzeczywistości również pęd elektronu będzie miał pewien rozrzut, którego wartość oznaczymy przez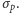

Zasada nieoznaczoności stwierdza, że gdybyśmy tak ustawili działo, żeby dostać jak najmniejsze 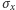(czyli by pomiary położenia prawie nie różniły się między sobą w kolejnych powtórzeniach doświadczenia), stałoby się to kosztem 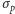(patrz rysunek). Wielkości te są powiązane: im dokładniej określone jest położenie cząstki, tym mniej dokładnie określony jest pęd, i vice versa [8]. Matematycznie stwierdzenie to zawiera się w nierówności

(*)

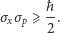Innymi słowy, iloczyn tych dwu wielkości nie może być dowolnie mały, lecz jest fundamentalnie ograniczony przez pewną stałą fizyczną, zwaną zredukowaną stałą Plancka. Wartość liczbowa tej stałej w skali doświadczanych przez człowieka wartości wielkości fizycznych jest niewiarygodnie mała, albowiem 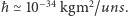Oznacza to, że z punktu widzenia naszych codziennych obserwacji można przyjąć, że w gruncie rzeczy prawa strona nierówności (*) wynosi zero, czyli nie ma żadnego związku między rozrzutam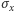i i 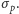Niemniej, gdy prowadzimy obserwacje w nanoskali, nie można już pominąć wartości 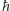i zasada nieoznaczoności ma znaczenie. Jest ona jednym z przejawów fundamentalnego indeterminizmu mechaniki kwantowej: nie da się przygotować cząstki w takim stanie, by wszystkie wielkości fizyczne były doskonale określone. Wręcz przeciwnie, są one nieoznaczone, pomiary od realizacji do realizacji doświadczenia dają różne wyniki, a ich rozrzuty można powiązać nierównością taką jak (*).

Powyższy wywód nie tłumaczy, dlaczego to akurat te dwie wielkości, czyli położenie i pęd połączone są zasadą nieoznaczoności. Dowód tego związku wymaga znajomości teorii przestrzeni Hilberta, lecz pewne argumenty na rzecz istnienia tego związku można oprzeć na wnioskach płynących z mechaniki klasycznej. Zauważmy, że to pęd (a zatem i prędkość) prowadzą do przesunięcia, czyli zmiany położenia - mówimy, że pęd jest generatorem przesunięcia. Mniej oczywisty jest związek odwrotny - zależność od położenia centralnej wielkości mechaniki klasycznej, jaką jest hamiltonian, generuje zmianę pędu. Z tych dwóch zdań wnioskujemy, że położenie i pęd nawet na gruncie mechaniki klasycznej są związane. Co więcej, można wykazać, że, na przykład, symetria przestrzenna układu (a zatem jego niezmienniczość pod wpływem transformacji przesunięcia) prowadzi do zasady zachowania pędu, i vice versa. Podobny związek zachodzi między składowymi wektora momentu pędu czy też energią a czasem. Stąd można się spodziewać, że istnieje wiele zasad nieoznaczoności, łączących rozrzuty pomiarów dwóch sprzężonych wielkości fizycznych.

Poza żywymi i martwymi kotami czy wysoce hipotetycznymi komputerami kwantowymi to zasada nieoznaczoności jest jednym z tych pojęć powstałych na gruncie teorii kwantów, które zdołały się przebić do powszechnej świadomości. Zazwyczaj formułowana jest w sposób niemający wiele wspólnego z powyższym wyprowadzeniem: powiada się, że pomiar położenia tak zaburza układ, że następujący po nim pomiar pędu daje wyniki z dużym rozrzutem, i na odwrót. Zauważmy, że w naszym opisie pomiary nie są wykonywane sekwencyjnie na jednej cząstce, lecz na wielu kopiach tego samego stanu kwantowego. Lecz bez względu na sformułowanie zasada nieoznaczoności Heisenberga pozostaje jedną ze zdumiewających konsekwencji kwantowej superpozycji.