Jeżeli widać korelację między rozdzielonymi przestrzennie zdarzeniami, to lokalny realizm wymusza konkluzję, że to rozdzielenie jest tylko pozorne. Np. odnajdując w bagażu tylko lewy kapeć, od razu wiem, że w domu został prawy, ale tak było od momentu zamknięcia walizki! Natomiast zgodnie z mechaniką kwantową mogę np. przygotować tzw. singletowy stan splątany dwóch ortogonalnych qubitów, o których nic więcej (poza ortogonalnością) nie wiadomo. Jednak w momencie pomiaru jednego, natychmiast wiem jaki jest ten drugi. Żeby qubity odróżnić od kapci, trzeba je mierzyć w innej bazie, niż zostały przygotowane. Np. jeżeli początkowo były to polaryzacje fotonów: pionowa i pozioma, to należy je rejestrować za pomocą polaryzatorów przekręconych o pewien (różny od 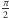) kąt względem pionu, żeby pojedynczy wynik nie był z góry znany. Wtedy średni poziom korelacji między pomiarami będzie łamał nierówności Bella (o których można myśleć jak o nierównościach trójkąta). Wynik jest w takim przypadku rezultatem analizy statystycznej wielu pojedynczych pomiarów.

Okazuje się, że można to zrobić inaczej: odwołując się do złożoności Kołmogorowa ciągów wyników i Złożoności tej, jako odpowiadającej najkrótszej sekwencji działań uniwersalnej maszyny Turinga generującej dany ciąg, zazwyczaj nie daje się obliczyć. Można ją jednak ograniczyć od góry przez długość 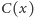skompresowanego ciągu 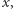bo im większy stopień korelacji, tym krótszy zapis po kompresji.

W ten sposób można zdefiniować 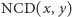(ang. Normalized Compression Distance), czyli "znormalizowaną odległość kompresyjną" dwóch ciągów 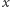i 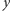(w tym przypadku są to binarne ciągi pomiarów każdego qubitu z kolejnych par) w poniższy sposób

gdzie 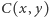jest skompresowaną długością połączonych ciągów 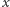i 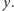Pomysł ten został pomyślnie przetestowany [1] z udziałem dwóch polskich fizyków. Stosowna nierówność okazała się być łamana.