Co to jest?
Co to jest sekunda i jak ją mierzymy
Czym jest sekunda? Dlaczego jej długość ciągle się zmienia? Jak działa zegar atomowy? Dlaczego pojedynczy pomiar sekundy może trwać kilkanaście minut? I dlaczego ostatecznie nigdy nie znamy aktualnego czasu?2

Zacznijmy od tego, czym jest zegar. Sprawa wydaje się prosta - w zegarach są mechanizmy, które działają okresowo. Co sekundę system przekładni albo układy scalone aktualizują czas. Przykładem może być wahadło: ramię wahadła oscyluje, porusza się w górę i w dół, w górę i w dół, a po każdym wahnięciu skomplikowany mechanizm porusza ostatnim z kół zębatych, do którego przyczepione są wskazówki. Czy to jest zegar? Niekoniecznie - to tylko mechanizm, który rusza wskazówkami. Od zegara wymagamy, żeby chodził dobrze, czyli żeby przesunięcie sekundowe wskazówki rzeczywiście odbywało się co sekundę. I tutaj pojawia się pytanie, czym w ogóle sekunda jest.
Definicję sekundy zmieniano już wielokrotnie. Często definicje opierały się na jakimś zjawisku fizycznym, które można obserwować z różnych części globu i co do którego spodziewamy się, że zawsze trwa tyle samo czasu, który na dodatek można dokładnie zmierzyć.
Dawna definicja sekundy oparta była na czasie, jakiego potrzebuje Ziemia, aby obrócić się wokół swojej osi, czyli na czasie trwania doby. Dokładniej, sekundą nazwano 1/86400 "średniego czasu słonecznego", czyli z grubsza średniego czasu trwania doby.
Mierzenie czasu w oparciu o tę definicję odbywa się z grubsza tak: mamy urządzenia, co do których spodziewamy się, że stabilnie wybijają takt, np. zegary wahadłowe, zegary kwarcowe, itd. W chwili gdy zaczyna się doba (początek doby jest arbitralnie określony, np. przez pojawienie się na horyzoncie jakiejś odległej gwiazdy), patrzymy na wskazania naszych urządzeń i mierzymy, ile "sekund" nasze urządzenie wskaże, gdy doba się skończy. Porównujemy wyniki tego pomiaru z liczbą 86400. Po wielu pomiarach może się okazać, że to, co nazywaliśmy zegarem, nie działa poprawnie. Na przykład może okazać się, że nasze urządzenie może "wybijać" więcej lub mniej "sekund" niż 86400 w ciągu doby, czyli że nasze urządzenie nie jest dokładne. Może się zdarzyć również, że nawet jeśli urządzenie średnio wskazało 86400 sekund na dobę, to z bardzo dużym odchyleniem, np. wśród pomiarów trwania doby mamy wyniki różniące się o dziesiątki sekund. Wtedy mówimy o zegarze, że jest niestabilny. Zauważmy, że zegar może być niedokładny i stabilny jednocześnie. Jeśli zegar wskazuje rzeczywiście 86400 sekund na dobę i jest przy tym stabilny, to można już go używać. Pamiętać trzeba jednak, żeby regularnie sprawdzać jego stabilność i dokładność.
Podsumowując: fizycy nazywają zegarem urządzenie, które nie tylko przestawia wskazówki na tarczy, ale jest regularnie kalibrowane, tzn. regularnie sprawdza się, że sekunda, którą mierzy zegar, zgadza się z definicją sekundy.
Obowiązująca definicja sekundy
Okazało się, że definicja sekundy oparta na czasie trwania doby jest niedoskonała. Chociażby z tego względu, że ruchy wody na powierzchni Ziemi, np. pływy, zmieniają czas trwania doby w praktycznie niemożliwy do przewidzenia sposób. Wynikające stąd nieregularności są małe, ale zauważalne. Powodują, że długość sekundy mierzona w oparciu o długość doby zmienia się co kilka lat o około 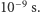 Ponadto pojawiły się pomysły, jak mierzyć sekundę znacznie dokładniej. W 1967 roku ogłoszono nową definicję sekundy. W przyjętym w polskim prawie brzmieniu
Ponadto pojawiły się pomysły, jak mierzyć sekundę znacznie dokładniej. W 1967 roku ogłoszono nową definicję sekundy. W przyjętym w polskim prawie brzmieniu
sekunda to czas równy 9192631770 okresom promieniowania odpowiadającego przejściu między dwoma poziomami struktury nadsubtelnej stanu podstawowego atomu cezu 133.
Domyślam się, że definicja może wydać się niejasna. Do jej zrozumienia wymagane są podstawy mechaniki kwantowej, w szczególności zaś fakt, że w układach związanych energia nie może być dowolna, może przyjąć tylko pewne dyskretne wartości. Te dozwolone wartości energii nazywamy poziomami energetycznymi. Ponad połowa przytoczonej definicji sekundy służy do jednoznacznego określenia, o jaki układ (atom cezu, izotop 133) i jakie jego poziomy (ze struktury nadsubtelnej stanu podstawowego) chodzi. Z dobrym przybliżeniem energia poziomów energetycznych atomów nie zależy od tego, gdzie układ się znajduje, jest więc uniwersalna.
Każdemu poziomowi energetycznemu odpowiada jakiś stan kwantowy, nazywany stanem stacjonarnym. Jeżeli układ jest w danym stanie, to ma energię odpowiadającą poziomowi energetycznemu. Znając stan układu, można obliczyć, co się w układzie tak naprawdę dzieje. W dużym uproszczeniu - w stanie podstawowym cezu elektrony są najbliżej jądra, jak tylko się da. Struktura nadsubtelna uwzględnia spin jądra atomu, który można sobie wyobrażać jako swego rodzaju wirowanie. Poziomy energetyczne składające się na strukturę nadsubtelną to poziomy różniące się ustawieniem spinu jądra względem elektronów.
Różnice między niektórymi poziomami łatwo obserwować, bo przekładają się na częstotliwość światła, jakie dany atom może pochłonąć lub wyświecić, przeskakując pomiędzy tymi poziomami. Stąd w definicji mowa o świetle. Czemu wybrano cez? Cóż, ten atom w czasach tworzenia definicji był popularny, miał dogodną strukturę poziomów energetycznych, istniały też rozwinięte metody manipulowania cezem. Obecnie oprócz cezu używa się innych atomów, np. rubidu, iterbu czy strontu. Zegary oparte na innych pierwiastkach i molekułach, a dopuszczone przez Międzynarodowe Biuro Miar i Wag, to tzw. zegary drugiego rodzaju.
Praktyczne wykorzystanie definicji
Do zrozumienia, jak rzeczywiście mierzona jest sekunda, potrzebny jest dalszy krótki kurs mechaniki kwantowej. Definicja mówi tylko o dwóch poziomach energetycznych. Wykorzystywane stany oznacza się zmienną 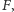 która tutaj może przyjąć wartości 3 lub 4. Jeśli atom jest w stanie
która tutaj może przyjąć wartości 3 lub 4. Jeśli atom jest w stanie 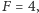 to jego energia
to jego energia 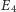 jest minimalnie większa niż energia stanu
jest minimalnie większa niż energia stanu 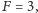 oznaczona
oznaczona 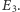 Mechanika kwantowa dopuszcza jednak stany "pośrednie", tzn. atom może być w superpozycji stanów
Mechanika kwantowa dopuszcza jednak stany "pośrednie", tzn. atom może być w superpozycji stanów 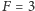 oraz
oraz 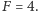 Jeśli atom jest w stanie superpozycji, to mierząc jego energię, zmierzymy albo
Jeśli atom jest w stanie superpozycji, to mierząc jego energię, zmierzymy albo 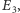 albo
albo 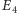 - wynik będzie losowy. Przygotowując ten sam stan superpozycji wielokrotnie, mierząc za każdym razem energię i uśredniając wyniki, otrzymamy liczbę między
- wynik będzie losowy. Przygotowując ten sam stan superpozycji wielokrotnie, mierząc za każdym razem energię i uśredniając wyniki, otrzymamy liczbę między 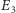 a
a 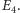
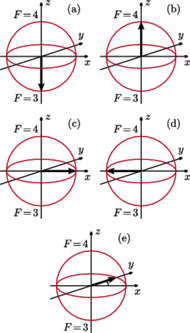
Graficzne przedstawienie stanów kwantowych dla układu o dwóch poziomach. Atom w stanie (a) 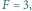 (b)
(b) 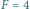 ; (c) to przykład równej superpozycji
; (c) to przykład równej superpozycji 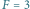 oraz
oraz 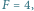 (d) stan zapoczątkowany w równej superpozycji po czasie równym połowie okresu, (e) stan zapoczątkowany w równej superpozycji po czasie równym jednej czwartej okresu.
(d) stan zapoczątkowany w równej superpozycji po czasie równym połowie okresu, (e) stan zapoczątkowany w równej superpozycji po czasie równym jednej czwartej okresu.
Takie układy, z dwoma poziomami energetycznymi, nazywamy kubitem. W rzeczywistości każdy atom, również cez, ma mnóstwo innych poziomów, ale fizycy z dobrym przybliżeniem mogą je odizolować. Definicja opiera się właśnie na takich poziomach, że gdy atom jest na którymś z nich, to samoistnie nie wskoczy na inny stan energetyczny spoza tych dwóch wyizolowanych. A jeśli z jakichś powodów zmieni stan, to używając innych wiązek laserowych i emisji spontanicznej, łatwo go "wepchnąć" z powrotem na jeden z dwóch stanów z definicji.
Układ o dwóch poziomach energetycznych można, na szczęście, łatwo zilustrować. Otóż każdy stan w układzie o dwóch poziomach można jednoznacznie reprezentować za pomocą wektora o długości 1. Zamiast pisać formułę określającą stan, rysuje się najczęściej sferę jednostkową (tzw. sferę Blocha), zaznaczając strzałką punkt na sferze, tak jak na rysunku obok. Pozwala to łatwo, przynajmniej w przypadku kubitów, sprowadzić mechanikę kwantową do geometrii. Układ odniesienia wybraliśmy tak, że jeśli atom jest w stanie 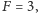 to odpowiada mu biegun południowy (rysunek (a)), jeśli w stanie
to odpowiada mu biegun południowy (rysunek (a)), jeśli w stanie 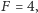 to biegun północny (rysunek (b)). Wszystkie pozostałe stany, stany superpozycji, leżą w innych miejscach sfery. Wśród nich ważnym stanem jest stan zaznaczony strzałką na rysunku (c). Odpowiada on tzw. równej superpozycji stanów
to biegun północny (rysunek (b)). Wszystkie pozostałe stany, stany superpozycji, leżą w innych miejscach sfery. Wśród nich ważnym stanem jest stan zaznaczony strzałką na rysunku (c). Odpowiada on tzw. równej superpozycji stanów 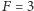 i
i 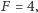 tzn. każdy z poziomów zostanie zmierzony z tym samym prawdopodobieństwem. Stan ten jest ważny, bo, po pierwsze, łatwo go przygotować w doświadczeniu, po drugie, jest używany przy pomiarze czasu. Ten stan nie jest stanem stacjonarnym, więc gdy atom przygotujemy w tym stanie, to za chwilę stan ten się zmieni. Dokładniej, dynamika takiego stanu wygląda tak, że pozostaje on na równiku, ale okrąża oś
tzn. każdy z poziomów zostanie zmierzony z tym samym prawdopodobieństwem. Stan ten jest ważny, bo, po pierwsze, łatwo go przygotować w doświadczeniu, po drugie, jest używany przy pomiarze czasu. Ten stan nie jest stanem stacjonarnym, więc gdy atom przygotujemy w tym stanie, to za chwilę stan ten się zmieni. Dokładniej, dynamika takiego stanu wygląda tak, że pozostaje on na równiku, ale okrąża oś  z dokładnie taką częstością jak ta z definicji sekundy. Jeśli więc przygotujemy stan z rysunku (c) i nic nie będziemy z atomem robić, to po czasie 1/9192631770 sekundy stan układu wróci do stanu z rysunku (c).
z dokładnie taką częstością jak ta z definicji sekundy. Jeśli więc przygotujemy stan z rysunku (c) i nic nie będziemy z atomem robić, to po czasie 1/9192631770 sekundy stan układu wróci do stanu z rysunku (c).
Doświadczalnicy potrafią manipulować na różne sposoby takimi atomami, np. mogą wywołać błyskawiczny obrót wokół osi 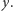 W tym celu potrzebują światła o częstości dopasowanej do różnicy energii między poziomami
W tym celu potrzebują światła o częstości dopasowanej do różnicy energii między poziomami 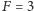 i
i 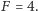 Zauważmy, że stan z rysunku (c), po obrocie o
Zauważmy, że stan z rysunku (c), po obrocie o 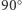 wokół osi
wokół osi 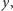 będzie leżał na biegunie północnym, czyli atom będzie w stanie
będzie leżał na biegunie północnym, czyli atom będzie w stanie 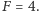 Z kolei jeśli pozwolimy stanowi z rysunku (c) ewoluować najpierw przez połowę okresu, a dopiero potem wykonamy obrót, to stan wpadnie na biegun południowy, czyli atom będzie w stanie
Z kolei jeśli pozwolimy stanowi z rysunku (c) ewoluować najpierw przez połowę okresu, a dopiero potem wykonamy obrót, to stan wpadnie na biegun południowy, czyli atom będzie w stanie 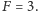
W zegarach czeka się przez czas równy 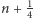 okresu, gdzie
okresu, gdzie  jest dużą liczbą naturalną, a następnie wykonuje się impuls obracający wokół osi
jest dużą liczbą naturalną, a następnie wykonuje się impuls obracający wokół osi 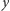 i ostatecznie mierzy się, w jakim stanie jest atom. Stan powinien wtedy pozostać na równiku, czyli powinien być ponownie w równej superpozycji (z nieistotną tutaj względną fazą między stanami nadsubtelnymi). Pomiar da z równym prawdopodobieństwem
i ostatecznie mierzy się, w jakim stanie jest atom. Stan powinien wtedy pozostać na równiku, czyli powinien być ponownie w równej superpozycji (z nieistotną tutaj względną fazą między stanami nadsubtelnymi). Pomiar da z równym prawdopodobieństwem 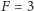 lub
lub 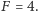 W praktyce wykorzystuje się dziesiątki tysięcy atomów naraz. Wtedy powinno się zmierzyć, że około połowy atomów jest w stanie
W praktyce wykorzystuje się dziesiątki tysięcy atomów naraz. Wtedy powinno się zmierzyć, że około połowy atomów jest w stanie 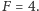 Właśnie taki pomiar jest sercem zegara atomowego. Jak widać, całość opiera się na ewolucji, która, notabene, często trwa znacznie krócej niż sekundę (to zależy od liczby
Właśnie taki pomiar jest sercem zegara atomowego. Jak widać, całość opiera się na ewolucji, która, notabene, często trwa znacznie krócej niż sekundę (to zależy od liczby  - czyli tego, ile pełnych okresów można poczekać przed impulsem obracającym wokół osi
- czyli tego, ile pełnych okresów można poczekać przed impulsem obracającym wokół osi 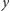 ). Zaraz po wytworzeniu stanu z rysunku (c) zaczyna się zliczać takty tzw. lokalnego oscylatora, czyli urządzenia, które niefizyk nazwałby po prostu zegarem. To urządzenie ma w sobie układy elektryczne, w których znajdują się kryształy. Drgania tych kryształów, o okresach rzędu nawet pikosekund, przekładają się na sygnały elektryczne wewnątrz obwodów. Częstość drgań można dodatkowo zmieniać. To urządzenie "kontaktuje" się z satelitami, aby uaktualniać bieżący czas. W momencie kiedy lokalny oscylator, czyli np. drgający kryształ w obwodzie elektrycznym, wykonał tyle taktów, że spodziewamy się, iż stan atomu cezu obrócił się o jedną czwartą pełnego obrotu wokół osi
). Zaraz po wytworzeniu stanu z rysunku (c) zaczyna się zliczać takty tzw. lokalnego oscylatora, czyli urządzenia, które niefizyk nazwałby po prostu zegarem. To urządzenie ma w sobie układy elektryczne, w których znajdują się kryształy. Drgania tych kryształów, o okresach rzędu nawet pikosekund, przekładają się na sygnały elektryczne wewnątrz obwodów. Częstość drgań można dodatkowo zmieniać. To urządzenie "kontaktuje" się z satelitami, aby uaktualniać bieżący czas. W momencie kiedy lokalny oscylator, czyli np. drgający kryształ w obwodzie elektrycznym, wykonał tyle taktów, że spodziewamy się, iż stan atomu cezu obrócił się o jedną czwartą pełnego obrotu wokół osi 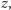 następuje strzał impulsem laserowym w atomy, który powoduje obrót stanu cezu wokół osi
następuje strzał impulsem laserowym w atomy, który powoduje obrót stanu cezu wokół osi 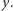 Zgodnie z tym, co napisaliśmy wyżej, oczekuje się, że w tym momencie połowa atomów będzie w stanie
Zgodnie z tym, co napisaliśmy wyżej, oczekuje się, że w tym momencie połowa atomów będzie w stanie 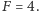 Prawie nigdy nie jest to jednak dokładnie połowa atomów. Wtedy automatycznie, dzięki tzw. pętli sprzężenia zwrotnego, częstość drgań kryształu jest odpowiednio korygowana. To wpływa z kolei na częstość światła używanego do wykonywania obrotów wokół osi
Prawie nigdy nie jest to jednak dokładnie połowa atomów. Wtedy automatycznie, dzięki tzw. pętli sprzężenia zwrotnego, częstość drgań kryształu jest odpowiednio korygowana. To wpływa z kolei na częstość światła używanego do wykonywania obrotów wokół osi 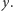 Przez szereg sprzężeń dąży się do tego, żeby częstość drgań lokalnego oscylatora była najczęściej, jak to możliwe, dopasowywana do częstości wzorcowej określonej w definicji sekundy.
Przez szereg sprzężeń dąży się do tego, żeby częstość drgań lokalnego oscylatora była najczęściej, jak to możliwe, dopasowywana do częstości wzorcowej określonej w definicji sekundy.
Cały eksperyment jest w istocie dość skomplikowany i samo przygotowanie atomów w stanie z rysunku (c) może trwać kilkanaście minut. Najwięcej czasu potrzeba na schłodzenie atomów do takich temperatur, żeby można było zaniedbać ich ruch i skupić się tylko na ich stanach wewnętrznych, 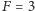 i
i 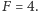 O tym, jak przygotować stan wielu atomów, by zwiększyć dokładność pomiaru, pisał w Delcie 5/2013 Jan Kołodyński.
O tym, jak przygotować stan wielu atomów, by zwiększyć dokładność pomiaru, pisał w Delcie 5/2013 Jan Kołodyński.
Obecnie w pomiarach wykorzystuje się chmury gazu, w których każdy atom jest przygotowany w stanie z rysunku (c). Okazuje się, że jeśli przygotować całą chmurę 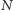 atomów tak, że stany atomów są ze sobą skorelowane, np. stan superpozycji: (wszystkie atomy w stanie
atomów tak, że stany atomów są ze sobą skorelowane, np. stan superpozycji: (wszystkie atomy w stanie 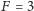 )
) 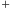 (wszystkie atomy w stanie
(wszystkie atomy w stanie 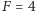 ), to dokładność można poprawić
), to dokładność można poprawić 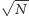 razy, zbliżając się do fundamentalnych ograniczeń wynikających z zasady nieoznaczoności Heisenberga.
razy, zbliżając się do fundamentalnych ograniczeń wynikających z zasady nieoznaczoności Heisenberga.
Gdy wreszcie jesteśmy pewni, że zegar działa poprawnie, można go użyć do pomiaru sekundy. Zawsze jednak pomiar jest obarczony niepewnością. Żeby uzgodnić, ile sekunda trwa, wyniki z najważniejszych zegarów atomowych są wysyłane do satelity, na którym dochodzi do uśredniania wskazań z różnych laboratoriów. Nową sekundę wykorzystuje się przez pewien czas do aktualizowania czasu globalnego. Notabene, robi się to wstecz, żeby obliczyć, jaki był czas kilka dni wcześniej.
Okazuje się, że czas globalny, bazujący na zegarach atomowych, różni się od wskazań starszych typów zegarów, opartych na obrocie Ziemi. Chcemy, żeby te dwa typy zegarów też były dość zgodne, bo o ile "czas atomowy" jest dokładniejszy, o tyle "ziemski" jest bardziej naturalny. Co kilka lat synchronizuje się oba systemy pomiaru czasu przez dodanie sekundy przestępnej do zegara atomowego. Dokładnie tak, jak dodaje się czasami dzień przestępny, 29 lutego. W ten sposób unikamy tego, że za kilkaset lat nasz zegarek zsynchronizowany z zegarem atomowym wskaże północ, mimo że Słońce będzie wysoko na niebie, jako że na zegarze ziemskim byłoby południe.
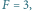 (b)
(b) 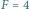 ; (c) to przykład równej superpozycji
; (c) to przykład równej superpozycji 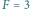 oraz
oraz 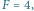 (d) stan zapoczątkowany w równej superpozycji po czasie równym połowie okresu, (e) stan zapoczątkowany w równej superpozycji po czasie równym jednej czwartej okresu.
(d) stan zapoczątkowany w równej superpozycji po czasie równym połowie okresu, (e) stan zapoczątkowany w równej superpozycji po czasie równym jednej czwartej okresu.