Nowości z przeszłości
Półwiecze
Za początek nowej, kwantowej ery w fizyce przyjmuje się zazwyczaj rok 1900. Wtedy to właśnie fizyk niemiecki Max Planck odkrył tak zwany kwant działania, którego wielkość, równa
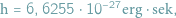
jest uniwersalną stałą fizyczną charakteryzującą procesy zachodzące w świecie obiektów mikroskopowych...
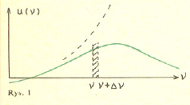
Przedstawiona dalej hipoteza Plancka wyjaśniała początkowo jedno tylko zjawisko fizyczne - rozkład energii promieniowania wysyłanego przez rozgrzane ciału fizyczne między różne częstotliwości tego promieniowania. Rozkład ten badano doświadczalnie,otrzymując w rezultacie krzywe w rodzaju przedstawionej linią ciągłą na Rys. 1.
Wielkość 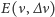 równa iloczynowi
równa iloczynowi 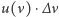 (pole zakreskowane na rysunku) jest ilością energii wypromieniowanej przez badane ciało w ciągu jednostki czasu, w zakresie częstotliwości od
(pole zakreskowane na rysunku) jest ilością energii wypromieniowanej przez badane ciało w ciągu jednostki czasu, w zakresie częstotliwości od  do
do 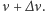
Zagadnienie to w teoretycznie wyidealizowanej formie, mianowicie przy założeniu, że promieniowanie elektromagnetyczne pozostaje w równowadze termodynamicznej z wysyłającym je ciałem, otrzymało nazwę zagadnienia promieniowania ciała doskonale czarnego, Według fizyki klasycznej - termodynamiki i elektrodynamiki - rozkład promieniowania ciała doskonale czarnego powinna opisywać krzywa dana wzorem Rayleigha-Jeansa
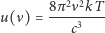
(linia przerywana na rys. 1), co stało w rażącej sprzeczności z wynikami doświadczalnymi. Zresztą wzór ten był sani w sobie paradoksalny, bowiem całkowita energia wypromieniowana w jednostce czasu, równa 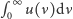 byłaby nieskończona. Paradoks ten nosi nazwę katastrofy w ultrafiolecie.
byłaby nieskończona. Paradoks ten nosi nazwę katastrofy w ultrafiolecie.
Jak pokazał Planck, promieniowanie ciała doskonale czarnego można opisać poprawnie, jeśli założyć, że atomy ciała drgające z częstotliwością e mogą przyjmować taki jedynie stan ruchu,by w każdej chwili ich energia była równa całkowitej wielokrotności wielkości 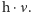
Promieniując lub pochłaniając promieniowanie atom taki może zmieniać swoją energię skokowo - znów o wielokrotność "kwantu energii"  Z założenia tego Planck wyprowadzi!swój słynny wzór
Z założenia tego Planck wyprowadzi!swój słynny wzór
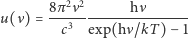
który doskonale zgadzał się z wynikami doświadczalnymi.
Zakaz przyjmowania energii różnej od 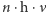 (
(  - liczba naturalna) był niezrozumiałym, wręcz paradoksalnym dodatkiem do doskonale niemal pięknego gmachu fizyki dziewiętnastowiecznej. Tymczasem coraz to nowe zjawiska świata obiektów mikroskopowych dawały się opisać przy założeniu takich niezrozumiałych, administracyjnych ograniczeń (zjawisko fotoelektryczne - Einstein, 1905; ciepło właściwe ciał w niskich temperaturach - Einstein, 1907; wreszcie model atomu - Bohr, 1913). Prawdziwa eksplozja zakazów i nakazów nastąpiła w optyce, gdzie przy pomocy takich pojęć jak "stany dozwolone" czy "przejścia wzbronione" wyjaśniano z powodzeniem strukturę widm atomowych. W systemie tym istniało wiele procesów fizycznych dających się opisać przez aparat matematyczny i pojęciowy teorii, jednak z niewiadomych powodów zabronionych przez jej część "administracyjną".
- liczba naturalna) był niezrozumiałym, wręcz paradoksalnym dodatkiem do doskonale niemal pięknego gmachu fizyki dziewiętnastowiecznej. Tymczasem coraz to nowe zjawiska świata obiektów mikroskopowych dawały się opisać przy założeniu takich niezrozumiałych, administracyjnych ograniczeń (zjawisko fotoelektryczne - Einstein, 1905; ciepło właściwe ciał w niskich temperaturach - Einstein, 1907; wreszcie model atomu - Bohr, 1913). Prawdziwa eksplozja zakazów i nakazów nastąpiła w optyce, gdzie przy pomocy takich pojęć jak "stany dozwolone" czy "przejścia wzbronione" wyjaśniano z powodzeniem strukturę widm atomowych. W systemie tym istniało wiele procesów fizycznych dających się opisać przez aparat matematyczny i pojęciowy teorii, jednak z niewiadomych powodów zabronionych przez jej część "administracyjną".
Ten stan rzeczy, zwany obecnie starszą teorią kwantów, nie mógł zadowolić fizyków. Poszukiwano teorii, w której obserwowane zakazy wynikałyby w konieczny sposób z samego sposobu opisu zjawisk.
W roku 1925 ukazała się praca młodego podówczas fizyka z Getyngi, Wernera Heisenberga "Über quantentheoretische Umdeutung kinematischer und mechanischer Beziehungen", a następnie dwie prace Heisenberga oraz Maxa Borna i Pasquala Jordana zatytułowane "Zur Quantenmechanik". Autorzy zaproponowali opis ruchu cząstek mikroskopowych w zupełnie nowym języku, różnym od mechaniki klasycznej. Z formalnego punktu widzenia nową teorię otrzymywali autorzy zastępując wielkości fizyczne takie jak położenie, pęd czy energia cząstki przez nieskończone macierze. Taka "mechanika macierzowa" pozwalała obliczyć poziomy energetyczne atomu wodoru czy oscylatora kwantowego (te ostatnie - nota bene - wynosiły 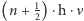 a nie - jak w hipotezie Plancka -
a nie - jak w hipotezie Plancka - 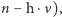 jednak sens matematyczny i pojęciowy wprowadzonych macierzy był jeszcze dość długo niejasny.
jednak sens matematyczny i pojęciowy wprowadzonych macierzy był jeszcze dość długo niejasny.
Tymczasem w roku 1926 pojawiła się seria prac Erwina Schrödingera, profesora na Politechnice w Zurychu, który proponował zastąpienie mechaniki klasycznej jeszcze inną teorią, nazwaną wkrótce mechaniką falową. Punktem wyjścia rozważań Schrödingera była zauważona już dawno analogia między mechaniką a optyką geometryczną.
Optyka geometryczna to bardzo nietypowa teoria fizyczna. Właściwie - to bardziej matematyka niż fizyka. Opisuje ona bieg promieni świetlnych w sytuacjach, gdy własności optyczne ośrodka bardzo mało zmieniają się na odległościach rzędu wielu długości fali świetlnej. Kształtem promieni rządzi zasada Fermata. Głosi ona, że spośród wszystkich linii łączących dwa wybrane punkty ośrodka promień świetlny pobiegnie po tej, dla której tak zwana droga optyczna jest najmniejsza. Droga optyczna jest całką ze współczynnika załamania:
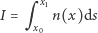
Na przykład w ośrodku jednorodnym, gdy 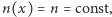 droga optyczna
droga optyczna 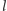 jest równa iloczynowi stałej
jest równa iloczynowi stałej 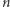 przez długość badanej linii. Oznacza to, że w tej sytuacji światło biegnie po liniach najkrótszych - prostych.
przez długość badanej linii. Oznacza to, że w tej sytuacji światło biegnie po liniach najkrótszych - prostych.
Stosując zasadę Fermata możemy projektować nawet bardzo skomplikowane urządzenia optyczne (obiektywy!) nie interesując się zupełnie fizyczną naturą światła.
W mechanice klasycznej istnieje ścisły odpowiednik zasady Fermata. Jest to tak zwana zasada Maupertuis-Lagrange'a. Głosi ona, że cząstka o masie  i energii całkowitej
i energii całkowitej 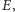 poruszająca się z punktu
poruszająca się z punktu 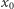 do
do 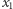 pod wpływem pola sił o potencjale
pod wpływem pola sił o potencjale 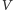 wybiera taki tor, na którym całka
wybiera taki tor, na którym całka
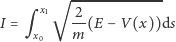
przybiera wartość minimalną. Wielkość 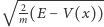 odgrywa tu jak gdyby rolę współczynnika załamania w punkcie
odgrywa tu jak gdyby rolę współczynnika załamania w punkcie 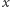 dla cząstek o energii
dla cząstek o energii 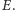
Optyka geometryczna nie nadaje się do opisu zjawisk interferencji i dyfrakcji, w których ujawnia się mikroskopowa struktura światła. Być może - rozumował Schrödinger - mechanika klasyczna jest właśnie "optyką geometryczną" prawdziwej, mikroskopowej mechaniki. Taki punkt widzenia sugerowały zresztą wcześniejsze prace młodego fizyka francuskiego, Louis de Broglie'a, który postulował rozważanie tak zwanych "fal materii". Schrödinger postawił sobie za cel znalezienie takiej "optyki fizycznej fał materii", dla której "optyką geometryczną" byłaby mechanika klasyczna. .
Zakładając możliwie najprostszą postać praw takiej optyki otrzymał równanie różniczkowe,zwane obecnie równaniem Schrödingera, którego rozwiązania opisywały na przykład poziomy energetyczne elektronu w atomie wodoru.
W kilka miesięcy później Schrödinger zauważył, że jego teoria - z pozoru tak różna od podejścia Heisenberga - jest w istocie rzeczy równoważna mechanice macierzowej.
Równoważność tę zbadali dokładniej P. A. M. Dirac i P. Jordan. Okazało się, że wszystkim obiektom matematycznym występującym w jednej z tych teorii można było przyporządkować odpowiednie obiekty drugiej i to w taki sposób, by równania opisujące prawa ruchu w obu teoriach przeszły wzajemnie na siebie.
Sytuacja była jednak bardzo dramatyczna. Rozwiązując równania Schrödingera lub Heisenberga otrzymywano na przykład częstotliwości linii widmowych prostych pierwiastków,jednak ani macierze Heisenberga, ani tajemnicza funkcja falowa 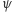 Schrödingera nie miały jasnej interpretacji fizycznej. Równania opisywały jakieś drgania - co gorsza zespolone, bowiem funkcja falowa przybiera wartości zespolone - ale nie wiedziano co tam mianowicie drga.
Schrödingera nie miały jasnej interpretacji fizycznej. Równania opisywały jakieś drgania - co gorsza zespolone, bowiem funkcja falowa przybiera wartości zespolone - ale nie wiedziano co tam mianowicie drga.
Wkrótce Schrödinger zauważył - ciągle jeszcze w tym samym, przełomowym roku 1426 - że z jego równania wynika prawo zachowania całki (rozciągniętej po całej przestrzeni) z kwadratu modułu funkcji falowej:
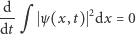 |
(1) |
Zaproponował zatem, by 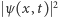 uważać za gęstość ładunku elektrycznego, dzięki czemu równanie (1) wyrażałoby prawo zachowania całkowitego ładunku. Elektron byłby więc grudką naładowanej materii o gęstości
uważać za gęstość ładunku elektrycznego, dzięki czemu równanie (1) wyrażałoby prawo zachowania całkowitego ładunku. Elektron byłby więc grudką naładowanej materii o gęstości 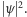
Taka interpretacja nie dała się jednak utrzymać. Przeczyło jej zbyt wiele faktów. Omówimy tu najprostszy z nich, tzw. rozpływanie się paczki fałowej.
Otóż w nieobecności sił zewnętrznych rozwiązania równania Schrödingera rozpływają się po całej przestrzeni niemal jak gaz doskonały, któremu dać dostatecznie dużo miejsca na rozprężenie. Istnieje na przykład rozwiązanie, dla którego rzekoma gęstość ładunku ma postać
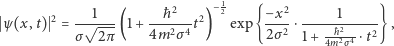
gdzie  jest masą elektronu,
jest masą elektronu, 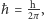 zaś
zaś 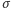 jest dowolną stałą o wymiarze długości. Poznajemy tu rozkład normalny Gaussa o dyspersji równej
jest dowolną stałą o wymiarze długości. Poznajemy tu rozkład normalny Gaussa o dyspersji równej
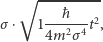
Gdyby nawet 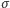 (dyspersja w chwili
(dyspersja w chwili 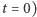 była mikroskopowo mała, to i tak po dostatecznie długim czasie możemy uzyskać dowolnie, makroskopowo wielką dyspersję. Dokonując pomiarów na takim elektronie, rozmytym na przykład na obszarze stu kilometrów, powinniśmy wykrywać zawsze tylko tę część ładunku, która leży w zasięgu naszej aparatury. Tymczasem nigdy nie zarejestrowano części ładunku elementarnego. We wszystkich znanych nam pomiarach ładunek elektronu pojawia się Zawsze jako całość. Widać to dobrze w doświadczeniach z dyfrakcją elektronów na kryształach, w których najlepiej manifestują się "falowe" własności materii (patrz "Delta" 10/75),
była mikroskopowo mała, to i tak po dostatecznie długim czasie możemy uzyskać dowolnie, makroskopowo wielką dyspersję. Dokonując pomiarów na takim elektronie, rozmytym na przykład na obszarze stu kilometrów, powinniśmy wykrywać zawsze tylko tę część ładunku, która leży w zasięgu naszej aparatury. Tymczasem nigdy nie zarejestrowano części ładunku elementarnego. We wszystkich znanych nam pomiarach ładunek elektronu pojawia się Zawsze jako całość. Widać to dobrze w doświadczeniach z dyfrakcją elektronów na kryształach, w których najlepiej manifestują się "falowe" własności materii (patrz "Delta" 10/75),
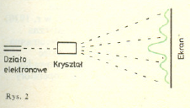

Linia falista na Rys. 2 przedstawia wartości funkcji 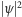 w różnych punktach ekranu. Wartości te w uderzający sposób zgadzają się z gęstością zaczernienia emulsji fotograficznej, którą pokryto ekran, proporcjonalną do ilości elektronów padających w danym punkcie. Zaczernienie to składa się jednak z dużej ilości pojedynczych plamek, z których każda świadczy o zarejestrowaniu jednego, całego, mikroskopowo małego elektronu.
w różnych punktach ekranu. Wartości te w uderzający sposób zgadzają się z gęstością zaczernienia emulsji fotograficznej, którą pokryto ekran, proporcjonalną do ilości elektronów padających w danym punkcie. Zaczernienie to składa się jednak z dużej ilości pojedynczych plamek, z których każda świadczy o zarejestrowaniu jednego, całego, mikroskopowo małego elektronu.
Zasadniczego przewrotu, który ostatecznie ukonstytuował mechanikę kwantową, zmieniając całkowicie sposób fizycznego opisu mikroświata dokonała hipoteza Maxa Borna o probabilistycznej interpretacji funkcji falowej. Zaproponował on - ciągle jeszcze w roku 1926 - by gęstość 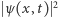 interpretować jako gęstość prawdopodobieństwa zarejestrowania elektronu(ale całego elektronu) w chwili
interpretować jako gęstość prawdopodobieństwa zarejestrowania elektronu(ale całego elektronu) w chwili 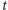 w punkcie
w punkcie 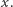 Dokładniej, liczba
Dokładniej, liczba
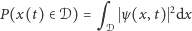 |
(2) |
równa jest prawdopodobieństwu zarejestrowania elektronu w chwili 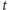 w obszarze
w obszarze 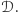 Dzięki równości (1) funkcja falowa daje się unormować, to znaczy pomnożyć przez taką stałą, by prawdopodobieństwo zarejestrowania elektronu gdziekolwiek (tzn. w całej przestrzeni) było stale równe jedności.
Dzięki równości (1) funkcja falowa daje się unormować, to znaczy pomnożyć przez taką stałą, by prawdopodobieństwo zarejestrowania elektronu gdziekolwiek (tzn. w całej przestrzeni) było stale równe jedności.
W tym momencie Rubikon został przekroczony. Fizyka mikroświata zerwała z tradycyjnym językiem, ukształtowanym dzięki potocznemu, makroskopowemu doświadczeniu i stała się teorią probabilistyczną. Dziwna to jednak probabilistyka - jakże różna od klasycznej teorii prawdopodobieństwa, której Uczymy się w szkole. "Teatrem działań"jest tu (podajemy współczesną wersję teorii) tak zwana przestrzeń Hilberta - abstrakcyjna przestrzeń wektorowa nad ciałem liczb zespolonych, na ogół nieskończenie wymiarowa. Jako konkretne przedstawienie takiej przestrzeni można wziąć na przykład zbiór schrödingerowskich funkcji falowych.
W przestrzeni Hilberta określony jest iloczyn skalarny, który parze wektorów 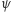 i
i 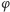 przyporządkowuje liczbę zespoloną oznaczaną zazwyczaj
przyporządkowuje liczbę zespoloną oznaczaną zazwyczaj 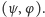 Zakłada się przy tym, że iloczyn skalamy jest:
Zakłada się przy tym, że iloczyn skalamy jest:
- 1.
- liniowy w pierwszym czynniku:
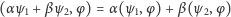
- 2.
- zmienia swą wartość na liczbę sprzężoną przy zamianie kolejności czynników:
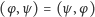
- 3.
- dodatnio określony, to znaczy
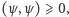 przy czym równość zachodzi tytko dla wektora zerowego.
przy czym równość zachodzi tytko dla wektora zerowego.
W przedstawieniu schrödingerowskim iloczyn skalamy dwu wektorów (funkcji fałowych) dany jest całką z iloczynu:
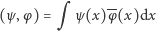
(całka rozciągnięta na całą przestrzeń).
Przestrzeń Hilberta ma wiele cech znanych nam przestrzeni euklidesowych. Dzięki iloczynowi skalarnemu można na przykład określić pojęcie długości wektora:
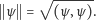
Można też mówić o prostopadłości wektorów, gdy ich iloczyn skalarny równy jest zeru. Ogólniej - można określić kąt 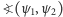 między dwoma kierunkami reprezentowanymi przez wektory
między dwoma kierunkami reprezentowanymi przez wektory 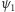 i
i 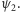 Przyjmujemy mianowicie
Przyjmujemy mianowicie
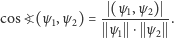 |
(3) |
Przez "kierunekżozumiemy tutaj całą jednowymiarową podprzestrzeń złożoną ze wszystkiej!wektorów proporcjonalnych do danego. Kierunek można reprezentować na przykład wektorach o długości jednostkowej: 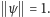
Wybór takiego reprezentanta oznacza, w języku funkcji falowych, spełnienie warunku unormowania gęstości prawdopodobieństwa, bowiem
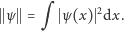
W ten sposób mechanika kwantowa stała się jak gdyby geometrią przestrzeni Hilberta. Stany opisywanego układu fizycznego (a przynajmniej tak zwane stany czyste) odpowiadają właśnie kierunkom w przestrzeni Hilberta. Każdym dwu stanom można przypisać liczbę dodatnią zawartą między zerem a jednością, zwaną prawdopodobieństwem przejścia. Jest ona równa kwadratowi kosinusa kąta zawartego między nimi. Reprezentując oba stany (kierunki) wektorami unormowanymi 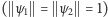 otrzymujemy zgodnie z (3) następującą wartość prawdopodobieństwa przejścia:
otrzymujemy zgodnie z (3) następującą wartość prawdopodobieństwa przejścia:
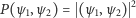
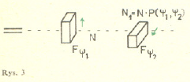
Aby zrozumieć sens fizyczny liczby 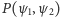 wyobraźmy sobie filtr
wyobraźmy sobie filtr 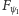 (Rys. 3), który z każdej wiązki elektronów przepuszcza tylko te, które są w stanie
(Rys. 3), który z każdej wiązki elektronów przepuszcza tylko te, które są w stanie 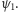 Niech - dla ustalenia uwagi -
Niech - dla ustalenia uwagi - 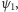 oznacza stan, w którym spin elektronu jest skierowany w górę, w kierunku osi
oznacza stan, w którym spin elektronu jest skierowany w górę, w kierunku osi 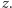 Filtrując dowolny strumień elektronów przez
Filtrując dowolny strumień elektronów przez 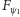 otrzymujemy wiązkę w stanie czystym, w której wszystkie spiny są skierowane w górę. Niech teraz
otrzymujemy wiązkę w stanie czystym, w której wszystkie spiny są skierowane w górę. Niech teraz 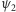 oznacza stan, odpowiadający innej, ale ustalonej konfiguracji spinu zaś
oznacza stan, odpowiadający innej, ale ustalonej konfiguracji spinu zaś 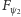 - odpowiedni filtr. Filtr ten jest oczywiście tym samym urządzeniem fizycznym co
- odpowiedni filtr. Filtr ten jest oczywiście tym samym urządzeniem fizycznym co 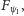 tylko nieco obróconym przestrzennie. Jak się okazuje, pewna część elektronów wiązki przefiltrowanej przez
tylko nieco obróconym przestrzennie. Jak się okazuje, pewna część elektronów wiązki przefiltrowanej przez 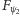 (a więc będących w stanie
(a więc będących w stanie 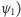 przejdzie również przez
przejdzie również przez 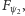 co oznacza, że są one w stanie
co oznacza, że są one w stanie 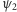 . Jak się obecnie wydaje, w przypadku pojedynczego elektronu nie potrafimy nigdy przewidzieć czy przejdzie on przez
. Jak się obecnie wydaje, w przypadku pojedynczego elektronu nie potrafimy nigdy przewidzieć czy przejdzie on przez 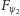 czy nie. Natomiast prawdopodobieństwo takiego przejścia jest równe właśnie
czy nie. Natomiast prawdopodobieństwo takiego przejścia jest równe właśnie 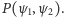
Taka kwantowa teoria prawdopodobieństwa wykazuje wiele zadziwiających własności, nieznanych w klasycznym rachunku prawdopodobieństwa. Trudno omówić je w krótkim artykule. Warto jednak wspomnieć, że ostateczny kształt pojęciowy zawdzięcza ona w dużej mierze P. A. M. Diracowi, którego piękna książka "Principles of Quantum Mechanics" (1 wyd. w r. 1930) była źródłem natchnienia dla wielu pokoleń fizyków i matematyków. Struktura matematyczna nowej teorii, przez długi czas nie w pełni zrozumiała, została zbadana przez Johna von Neumanna, który właśnie pod koniec lat 20-tych był asystentem wielkiego Dawida Hilberta w Getyndze i tam zetknął się osobiście z twórcami mechaniki kwantowej. Właśnie von Neumann wprowadził pojęcie abstrakcyjnej przestrzeni Hilberta, zinterpretował "macierze" Heisenberga jako operatory w tej przestrzeni i zbadał ich własności, co dało początek nowemu działowi analizy funkcjonalnej.
Ciekawe, że sam Hilbert w swej teorii równań całkowych, opublikowanej dwadzieścia lat przed powstaniem mechaniki kwantowej, wprowadził pojęcie tak zwanego widma formy kwadratowej. Jak się okazało, energia atomu wyraża się właśnie przez formę kwadratową, której widmo (w sensie Hilberta) odpowiada obserwowanemu w spektroskopie widmu promieniowania wysyłanego przez świecące atomy.
Genialna intuicja Hilberta objawiła się jeszcze raz w roku 1925, gdy Bom i Jordan próbowali zasięgnąć jego rady w sprawie pewnych trudności matematycznych związanych z macierzami nieskończonymi. Hilbert odpowiedział wówczas, że jedynym miejscem, gdzie takie macierze pojawiają się w sposób naturalny, jest teoria równań. Nakłaniał więc fizyków do szukania odpowiedniego równania różniczkowego - właśnie późniejszego równania Schrödingera - jednak Bom i Jordan nie potraktowali wówczas tej rady poważnie. Mechanika kwantowa, a nawet jej wersja relatywistyczna podana w roku 1928 przez Diraca, nie rozwiązała bynajmniej wszystkich trudności opisu mikroświata. Wiele kłopotów filozoficzno-pojęciowych nastręczał fakt, że funkcję falową potrafimy przypisać jedynie zespołom statystycznym - na przykład zbiorowi cząstek produkowanych przez dany akcelerator, przy ustalonych parametrach makroskopowych, takich jak napięcia przyspieszające, szerokości szczelin kolimatorów itp. Natomiast próby zdefiniowania funkcji falowej pojedynczego mikroobiektu - na przykład przypadkowo zbłąkanej cząstki promieniowania kosmicznego - prowadziły do paradoksalnych wniosków - słynne są paradoksy Einsteina-Rosena-Podolsky'ego (patrz artykuł G. Białkowskiego) oraz Schrödingera. Jak dotychczas jednak próby zastąpienia mechaniki kwantowej czymś innym nie powiodły się. Wyjaśniając ogromną ilość zjawisk z tak różnych dziedzin jak optyka, teoria ciała stałego, fizyka jądrowa jest ona obecnie "wzorcową" teorią mikroskopową. Na jej obraz i podobieństwo budujemy teorie opisujące systemy nawet dużo bardziej skomplikowane niż mechaniczne układy kilku cząstek (pole elektromagnetyczne). Kryje się w tym jednak ogromna ilość zagadek i niejasności dotychczas nie rozwiązanych.