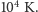W obszarze temperatur bliskich temperaturze pokojowej molowe ciepło właściwe w stałej objętości gazów dwuatomowych jest z dobrym przybliżeniem równ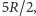e gdzie 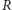jest tzw. stałą gazową. Można wyjaśniać to na gruncie fizyki klasycznej za pomocą zasady ekwipartycji energii - składająca się z dwóch punktowych atomów cząsteczka ma pięć stopni swobody: trzy związane z przesunięciami całej cząsteczki w przestrzeni oraz dwa związane z ustawieniem osi łączącej atomy. W równowadze termicznej w temperaturze 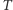średnia energia cząsteczki jest równa iloczynowi czynnika 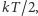gdzie 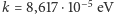/K jest stałą Boltzmanna, i liczby stopni swobody, zatem ciepło właściwe w stałej objętości, czyli energia potrzebna do podgrzania jednego mola ( 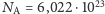cząsteczek) o 1 K, jest równa właśnie 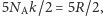gdzie skorzystaliśmy z relacji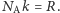

Przedstawione powyżej rozumowanie pozwoliło Rudolfowi Clausiusowi wysunąć w latach osiemdziesiątych XIX wieku przypuszczenie, że tlen i azot składają się właśnie z cząsteczek dwuatomowych, a gazy, których ciepło właściwe wynosi 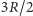- z pojedynczych atomów. Tymczasem w temperaturach niższych od pokojowej przewidywanie to nie musi być poprawne - wystarczy spojrzeć choćby na zależność od temperatury ciepła właściwego wodoru przedstawioną na rysunku.

Wyjaśnienie takiej zależności musi odwołać się do mechaniki kwantowej, przewidującej skwantowanie niektórych wielkości charakteryzujących ruch cząsteczki - w tym przypadku związanych z jej obrotem. Moment pędu 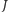jest bowiem zawsze całkowitą wielokrotnością wartości :

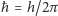Zasadę ekwipartycji energii można zaś stosować jedynie wtedy, gdy temperatura 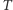jest na tyle wysoka, że energia termiczna 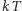przekracza energię najniższego stanu wzbudzonego związanego z rozważanym stopniem swobody. Jeżeli wartość 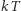jest mniejsza od energii najniższego stanu wzbudzonego, to odpowiadający mu stopień swobody jest "zamrożony" i nie daje wkładu do ciepła właściwego. Dla stanów rotacyjnych cząsteczki najniższy stan odpowiada 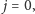a pierwszy stan wzbudzony 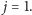Oszacujmy energię stanu rotacyjnego o momencie pędu 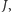posługując się mechaniką klasyczną:

gdzie 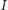oznacza moment bezwładności cząsteczki. Stany rotacyjne nie dają wkładu do ciepła właściwego, gdy 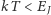dla najniższej różnej od zera wartości 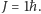Wśród gazów dwuatomowych najmniejszy moment bezwładności, a więc i najwyższą energię wzbudzeń rotacyjnych ma cząsteczka wodoru H 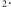Jej moment bezwładności to:

gdzie 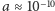m jest typową odległością jąder atomów cząsteczek dwuatomowych (długością wiązania), 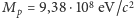to zaś masa protonu. Otrzymujemy więc, że dla

molowe ciepło właściwe gazów dwuatomowych będzie takie jak gazów jednoatomowych. Po podstawieniu danych liczbowych otrzymamy 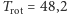K; dokładniejsze obliczenia uwzględniające długość wiązania 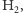czyli 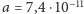m, oraz fakt, że zgodnie z mechaniką kwantową wartość kwadratu momentu pędu to 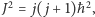prowadzą (dla wodoru) do wartości 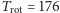K. Dla pozostałych cząsteczek dwuatomowych granica ta jest kilka do kilkudziesięciu razy niższa. Niewyjaśnioną zagadką pozostawało, dlaczego w rozumowaniach takich jak rozumowanie Clausiusa dla uzyskania zgodności z doświadczeniem należało rozważać tylko ruch postępowy i obrotowy, a pomijać drgania cząsteczek i wzbudzenia elektronów. Rozwiązanie tej zagadki wykracza poza możliwości fizyki klasycznej.