Niedawno ukazała się praca [1], w której autorzy dowodzą, że w świecie kwantowym powinno być inaczej, o ile zadowalamy się informacją dotyczącą jedynie korelacji między kwantowymi "gołębiami".

Rozpatrzmy trzy rozróżnialne cząstki. Na początku każdą przygotowujemy w superpozycji dwóch stanów (cząstka w lewej "przegródce": 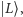w prawej: ):

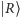Uwaga. W stosowanym tu zapisie Diraca, 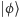(tzw. ket) oznacza funkcję falową Funkcja falowa sprzężona 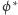jest zapisywana jako 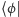(tzw. bra), więc moduł funkcji falowej (prawdopodobieństwo) to 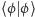(czyli bra ket). Użyteczność zapisu wynika m.in. z łatwości zapisu operatora rzutującego 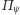na stan 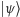(operatora mierzącego, ile jest stanu w badanym stanie) jako 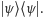Np. pomiar, ile jest stanu 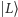w stanie 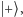daje następujący, łatwy do przerachowania (i oczekiwany) wynik:

Wracając do głównego wątku, początkowy stan trzech cząstek można zapisać jako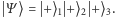

Na końcu dokonujemy sprawdzenia, czy każda z cząstek jest w stanie 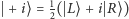(ortogonalnym do analogicznie zdefiniowanego stanu ).

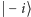Raz na osiem razy otrzymamy wynik

W takim przypadku możemy zastanowić się, czy jakaś para cząstek była w tej samej przegródce. Wobec symetrii układu wynik będzie taki sam dla każdej z trzech par. Taka para może być albo w lewej, albo w prawej przegródce, więc stosowny operator rzutujący (dla pary 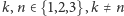) ma postać

gdzie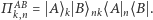

Analogicznie można zapisać operator sprawdzający, czy cząstki te były osobno:

Bezpośrednim rachunkiem łatwo wykazać, że:

oraz

czego można było się spodziewać, podczas gdy:

Czyli między początkowym ustawieniem 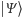a końcowym pomiarem 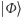każda para cząstek była osobno, choć cząstek było trzy w dwóch przegródkach!?!

Jeżeli wynik końcowego pomiaru wyszedłby inny np. 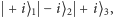to pary 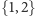oraz 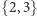byłyby między pomiarami razem, ale para 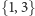osobno, co, według klasycznej logiki, również jest nie do pojęcia (tego typu sytuacja zdarza się 6, a poprzednio omówiona 2 razy na 8 możliwości).

Jest to wcześniej niezauważony aspekt kwantowego splątania. Tym razem chodzi bardziej o splątanie czasowe niż przestrzenne. Wynik zależy nie tylko od tego, co przedtem, ale również od tego, co potem. Należy jednak od razu ostudzić zapał entuzjastów SF. To nie jest droga do podróży w czasie. Wszystko dzieje się w ramach nieoznaczoności Heisenberga.

Zauważmy jednak, że ta zaskakująca własność teorii kwantowej pojawia się tylko dlatego, że nie pytamy o to, w której przegródce znajduje się która cząstka. Pytamy wyłącznie o korelacje między cząstkami, które w żaden inny sposób skorelowane ze sobą nie są.

W omawianej pracy [1] podane są nawet propozycje doświadczalnej obserwacji zjawiska poprzez oddziaływanie cząstek wtedy, gdy są razem. Czekamy.