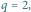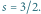Fraktale kwantowe
Czy funkcje fraktalne mają cokolwiek wspólnego z opisem zjawisk w rzeczywistości? Okazuje się, że tak. Funkcje fraktalne mogą opisywać stany kwantowe prostych obiektów, np. cząstki w pudełku...
W wyniku edukacji szkolnej można nabrać przekonania, że świat pełen jest gładkich obiektów, dobrze opisywanych przez linie proste, płaszczyzny, koła, kule itd. Poprosiwszy kogoś o narysowanie typowego wykresu funkcji, zwykle otrzymamy wykres wielomianu lub złożenia najbardziej znanych funkcji gładkich. A jednak, ściśle rzecz biorąc, typowa funkcja nie jest nigdzie ciągła, typowa funkcja ciągła nie jest nigdzie różniczkowalna itd. Odkrycie to było szokiem dla wielu matematyków, którzy jeszcze niewiele ponad sto lat temu uważali, że wszystkie funkcje ciągłe są różniczkowalne (opinię tę do dziś podziela wielu studentów na egzaminach analizy matematycznej).
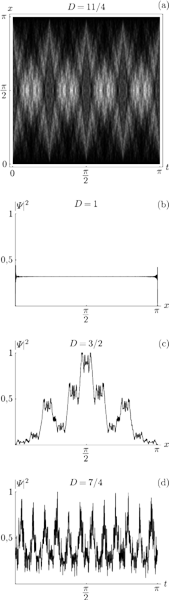
Rys. 1 (a) Fraktalny dywan kwantowy dla cząstki w pudełku, jaśniejszy odcień oznacza większą
gęstość prawdopodobieństwa; (b) i (c) cięcia przestrzenne dywanu w
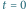 i
i
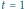 ; (d) cięcie czasowe w
; (d) cięcie czasowe w
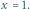
Rysunki otrzymano, składając 200 początkowych składników we wzorze (9).
Podstawy analizy matematycznej uporządkowano w drugiej połowie XIX wieku i wtedy zaczęto odróżniać funkcje różniczkowalne od ciągłych. Naturalnie pojawiło się pytanie, czy istnieją ciągłe funkcje, które nie są nigdzie różniczkowalne. Pierwszą osobą, która rozważała ten problem, był prawdopodobnie Riemann. W 1861 r. postawił hipotezę, że funkcja
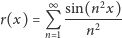 | (1) |
jest ciągła, ale nieróżniczkowalna, jednak nie był w stanie tego udowodnić. W 1872 r. Weierstrass podał inną funkcję, noszącą dziś jego nazwisko,
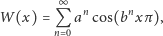 | (2) |
i udowodnił, że dla pewnych wartości
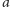 i
i
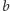 nie jest
ona różniczkowalna dla żadnego
nie jest
ona różniczkowalna dla żadnego
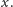 Kolejny krok wykonał
Godfrey Hardy (1877–1947), który udowodnił nieróżniczkowalność
Kolejny krok wykonał
Godfrey Hardy (1877–1947), który udowodnił nieróżniczkowalność
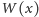 dla wszystkich wartości
dla wszystkich wartości
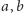 spełniających warunki
spełniających warunki
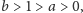
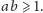 Dostarczył on również dowodu
nieróżniczkowalności funkcji
Dostarczył on również dowodu
nieróżniczkowalności funkcji
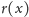 dla dowolnego niewymiernego
dla dowolnego niewymiernego
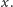 Później pokazano, że
Później pokazano, że
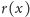 jest różniczkowalna dla
pewnych wymiernych wartości
jest różniczkowalna dla
pewnych wymiernych wartości
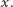
Hardy nie tylko wykazał nieróżniczkowalność
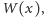 ale też
zmierzył ją: udowodnił mianowicie, że
ale też
zmierzył ją: udowodnił mianowicie, że
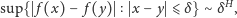 | (3) |
gdzie

Korzystając z tego wyniku, można wykazać, że wymiar pudełkowy
(opisany w artykule Krzysztofa Barańskiego) wykresu funkcji Weierstrassa
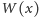 wynosi
wynosi
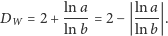 | (4) |
Funkcje, których wykresy mają niecałkowity wymiar pudełkowy, nazywamy funkcjami fraktalnymi.
Czy jednak ma to cokolwiek wspólnego z opisem zjawisk w rzeczywistości?
Okazuje się, że funkcje fraktalne mogą opisywać stany kwantowe prostych
obiektów, np. cząstki w pudełku. Zanim to pokażemy, przypomnijmy
podstawowe zasady mechaniki kwantowej. W mechanice klasycznej żeby
opisać stan układu, musimy podać położenia i prędkości wszystkich jego
elementów składowych. Jeżeli znamy wszystkie siły działające w układzie,
możemy wyznaczyć jego przyszły stan, korzystając z praw Newtona, czyli
rozwiązując równania ruchu. W mechanice kwantowej stan układu
opisywany jest przez zespoloną funkcję falową
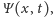 której
ewolucję opisuje równanie Schrödingera. Kwadrat modułu funkcji falowej,
której
ewolucję opisuje równanie Schrödingera. Kwadrat modułu funkcji falowej,
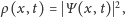 jest gęstością prawdopodobieństwa zaobserwowania
układu w danym punkcie
jest gęstością prawdopodobieństwa zaobserwowania
układu w danym punkcie
 w chwili
w chwili
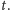
Rys. 2 (a) Fraktalny dywan kwantowy dla cząstki w pudełku; (b) średnia prędkość;
(c) i (d) cięcia przestrzenne w
 i
i
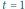 ; (e) i (f) cięcia czasowe w
; (e) i (f) cięcia czasowe w
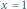 i
i
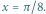 Wykresy otrzymano, składając pierwsze 20 składników we
wzorze (10) dla
Wykresy otrzymano, składając pierwsze 20 składników we
wzorze (10) dla
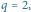
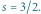
Rozważmy jeden z najprostszych modeli fizycznych: poruszającą się w jednym
wymiarze cząstkę o masie
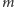 w pudełku o nieskończenie sztywnych
ściankach,a więc układ mechaniczny z potencjałem
w pudełku o nieskończenie sztywnych
ściankach,a więc układ mechaniczny z potencjałem
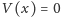 dla
dla
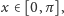 poza tym
poza tym
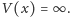 Wszystkie rozwiązania równania
Schrödingera dla tego układu są postaci
Wszystkie rozwiązania równania
Schrödingera dla tego układu są postaci
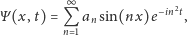 | (5) |
gdzie
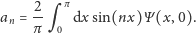 | (6) |
W 1996 roku Michael Berry zauważył, że jeżeli w chwili
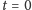 wiemy
o cząstce jedynie tyle, że jest ona gdzieś w pudełku, to wówczas jej stan
początkowy możemy opisać funkcją falową,
wiemy
o cząstce jedynie tyle, że jest ona gdzieś w pudełku, to wówczas jej stan
początkowy możemy opisać funkcją falową,
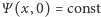 wewnątrz
pudełka oraz
wewnątrz
pudełka oraz
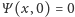 na zewnątrz. Wtedy gęstość prawdopodobieństwa
na zewnątrz. Wtedy gęstość prawdopodobieństwa
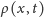 znalezienia cząstki w punkcie
znalezienia cząstki w punkcie
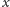 dla ustalonego czasu
dla ustalonego czasu
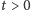 jest prawie zawsze funkcją fraktalną, której wykres ma wymiar
jest prawie zawsze funkcją fraktalną, której wykres ma wymiar
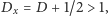 gdzie
gdzie
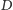 jest wymiarem przestrzeni (u nas
jest wymiarem przestrzeni (u nas
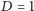 ). Z kolei, jeżeli ustalimy punkt
). Z kolei, jeżeli ustalimy punkt
 w przestrzeni, to prawie
zawsze wykres gęstości prawdopodobieństwa w tym punkcie jest funkcją
fraktalną o wymiarze pudełkowym
w przestrzeni, to prawie
zawsze wykres gęstości prawdopodobieństwa w tym punkcie jest funkcją
fraktalną o wymiarze pudełkowym
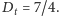
W opisywanym przypadku funkcja falowa Berry’ego ma w chwili
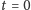 postać
postać
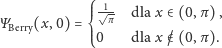 | (7) |
Z równania (6) otrzymujemy
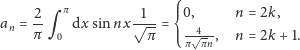 | (8) |
Zatem
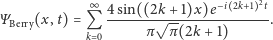 | (9) |
Dlaczego tak prosty stan początkowy staje się fraktalem podczas liniowej ewolucji
zadanej równaniem Schrödingera? W istocie stan początkowy jest nieciągły na
brzegu pudełka, co jest przyczyną omówionych wyżej fraktalnych własności
stanu układu. Żeby złożyć funkcję stałą na odcinku z funkcji bazowych
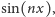 musimy wziąć ich nieskończenie wiele. Kiedy przybliżamy
funkcję falową skończoną sumą sinusów, im bliżej brzegów, tym gorzej nam
to wychodzi. Jest to tak zwany efekt Gibbsa, znany z analizy Fouriera.
Ponieważ ewolucja kwantowa zmienia fazy każdej funkcji składowej
proporcjonalnie do energii stanu, w każdej chwili
musimy wziąć ich nieskończenie wiele. Kiedy przybliżamy
funkcję falową skończoną sumą sinusów, im bliżej brzegów, tym gorzej nam
to wychodzi. Jest to tak zwany efekt Gibbsa, znany z analizy Fouriera.
Ponieważ ewolucja kwantowa zmienia fazy każdej funkcji składowej
proporcjonalnie do energii stanu, w każdej chwili
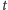 stan układu jest
sumą nieskończonej liczby oscylacji o praktycznie losowych fazach, co prowadzi
do fraktala. Okazuje się też, że energia stanu opisanego funkcją Berry’ego
jest nieskończona.
stan układu jest
sumą nieskończonej liczby oscylacji o praktycznie losowych fazach, co prowadzi
do fraktala. Okazuje się też, że energia stanu opisanego funkcją Berry’ego
jest nieskończona.
Można tu zadać kilka pytań. Czy nieciągłość stanu początkowego jest koniecznym warunkiem fraktalności? Czy może raczej nieskończona energia? Czy wymiar fraktalny funkcji falowej jest zdeterminowany wymiarem przestrzeni? Okazuje się, że nieskończona energia stanu jest konieczna, żeby stan był „prawdziwym” fraktalem: funkcja falowa musi mieć składowe o dowolnie dużej energii (wysokiej częstości przestrzennej), żeby skalowanie występowało w najmniejszych skalach, a przy tym wagi składowych muszą być na tyle duże, żeby pochodna funkcji falowej nie była różniczkowalna. Natomiast można znaleźć fraktalne funkcje falowe wszędzie ciągłe o dowolnym dozwolonym wymiarze fraktalnym. (Jasne jest, że wykres ciągłej rzeczywistej funkcji musi mieć wymiar nie mniejszy niż wymiar prostej, czyli 1, a nie może być większy niż wymiar przestrzeni, w której leży, czyli 2.)
Przykładową klasę funkcji falowych o zadanym wymiarze otrzymamy, biorąc dla cząstki w pudełku stan początkowy opisany funkcją Weierstrassa (2). Wówczas
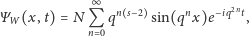 | (10) |
gdzie
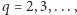
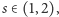 a
a
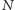 jest stałą normalizacji.
Funkcja (10) ma kilka ciekawych własności. Okazuje się, że jej część
rzeczywista i urojona, a także kwadrat jej modułu, czyli gęstość
prawdopodobieństwa, są funkcjami fraktalnymi. Dla dowolnego ustalonego
czasu
jest stałą normalizacji.
Funkcja (10) ma kilka ciekawych własności. Okazuje się, że jej część
rzeczywista i urojona, a także kwadrat jej modułu, czyli gęstość
prawdopodobieństwa, są funkcjami fraktalnymi. Dla dowolnego ustalonego
czasu
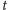 wykres przestrzennej zależności funkcji
wykres przestrzennej zależności funkcji
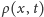 jest
fraktalem o wymiarze
jest
fraktalem o wymiarze
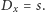 Dla prawie każdego ustalonego
Dla prawie każdego ustalonego
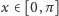 wykres funkcji
wykres funkcji
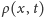 jest fraktalem o wymiarze
jest fraktalem o wymiarze
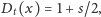 ale dla gęstego, dyskretnego zbioru punktów
ale dla gęstego, dyskretnego zbioru punktów
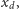 funkcja
funkcja
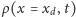 jest gładka, a więc
jest gładka, a więc
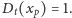 Wykres
funkcji dwóch zmiennych
Wykres
funkcji dwóch zmiennych
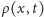 jest fraktalem o wymiarze
jest fraktalem o wymiarze
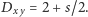
Dwuwymiarowe wykresy gęstości prawdopodobieństwa
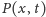 nazywamy
fraktalnymi dywanami kwantowymi, w analogii do pojęcia dywanów
kwantowych używanego w przeszłości. Na rysunku 2(a) pokazujemy
typowy fraktalny dywan kwantowy (jaśniejsze obszary oznaczają większą
gęstość prawdopodobieństwa) dla
nazywamy
fraktalnymi dywanami kwantowymi, w analogii do pojęcia dywanów
kwantowych używanego w przeszłości. Na rysunku 2(a) pokazujemy
typowy fraktalny dywan kwantowy (jaśniejsze obszary oznaczają większą
gęstość prawdopodobieństwa) dla
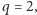
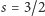 i jego
cięcia w czasie i przestrzeni. Okresowość w czasie z okresem
i jego
cięcia w czasie i przestrzeni. Okresowość w czasie z okresem
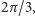 którą widzimy na dywanie, wiąże się ze strukturą widma częstości
którą widzimy na dywanie, wiąże się ze strukturą widma częstości
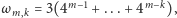
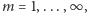
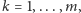 fraktalnej
gęstości prawdopodobieństwa
fraktalnej
gęstości prawdopodobieństwa
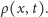 W punktach
W punktach
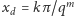 (
(
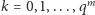 ) suma (10) ma tylko
) suma (10) ma tylko
 składników, w związku
z czym funkcja
składników, w związku
z czym funkcja
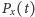 jest gładka (
jest gładka (
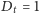 ). Przykład
takiego zachowania pokazany jest na rysunku 2(f). Tak więc funkcja
). Przykład
takiego zachowania pokazany jest na rysunku 2(f). Tak więc funkcja
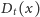 nie jest ciągła w żadnym punkcie
nie jest ciągła w żadnym punkcie
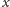 na przedziale
na przedziale
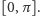
Oczywiście, żaden układ nie może mieć nieskończonej energii, co, między innymi, oznacza, że nie ma w przyrodzie „prawdziwych” fraktali, tak samo, jak nie ma idealnych okręgów, prostych itd. W praktyce mówimy o fraktalach „fizycznych”, mając na myśli obiekty, które w pewnym zakresie skali wykazują (statystyczne) samopodobieństwo. Ciekawe, że te fizyczne fraktale kwantowe, zdefiniowane jako skończone sumy składników w równaniu (10), zachowują swój charakter w czasie. Podobne rozwiązania można skonstruować dla całej klasy potencjałów wiążących cząstkę wystarczająco mocno (np. dla oscylatora harmonicznego).
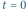 i
i
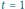 ; (d) cięcie czasowe w
; (d) cięcie czasowe w
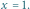
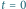 i
i
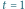 ; (e) i (f) cięcia czasowe w
; (e) i (f) cięcia czasowe w
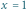 i
i
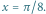 Wykresy otrzymano, składając pierwsze 20 składników we
wzorze (10) dla
Wykresy otrzymano, składając pierwsze 20 składników we
wzorze (10) dla