W tej skali siła grawitacji jest za słaba, żeby obserwować efekty jej działania. Oddziaływanie grawitacyjne jest zdominowane przez oddziaływanie elektromagnetyczne i oddziaływanie silne. Rozważania teoretyczne przewidują, że pole grawitacyjne powinno prowadzić do stanów kwantowych, podobnych jak dla elektronów w polu elektromagnetycznym i nukleonów w polu oddziaływań silnych. Jednak aby zaobserwować efekty kwantowe pola grawitacyjnego, trzeba wyeliminować wpływ innych pól. Do przeprowadzenia doświadczeń mających na celu badanie efektów kwantowych grawitacji nadają się neutrony, ponieważ mają długi średni czas życia (około 1000 s), są obojętne elektrycznie i mają dużą masę )

Pierwsze doświadczenie, którego celem było zaobserwowanie powiązania między zjawiskami kwantowo-mechanicznymi a grawitacją, zostało opisane w 1975 roku i dotyczyło interferencji neutronów znajdujących się w polu grawitacyjnym Ziemi. Drugie doświadczenie zostało przeprowadzone w ostatnich latach przez zespół V.V. Nesvizhevsky’ego w Instytucie Laue-Langevin (ILL) w Grenoble (Francja) [2, 3]. W tym drugim doświadczeniu użyto ultrazimnych neutronów (UCN – ultracold neutrons), generowanych przez ich źródło, dostępne w ILL w Grenoble. Takie neutrony mają tak małe wartości energii kinetycznej, że mogą zostać uwięzione przez grawitację, tak jak odbijająca się od podłogi piłka.

Oprócz pola grawitacyjnego potrzebna jest jeszcze „podłoga” pułapki, którą może być poziome zwierciadło neutronowe. Ponieważ długość fali de Broglie’a dla zimnych neutronów jest większa od odległości międzyatomowych w ciele stałym, to oddziaływanie neutronów z takim ciałem można opisywać za pomocą efektywnego potencjału, a nie oddziaływania z poszczególnymi jądrami. Jeżeli siła odpychająca pochodząca od bariery potencjału jest większa niż energia kinetyczna obliczona tylko dla składowej prędkości prostopadłej do powierzchni zwierciadła, to neutron zostanie odbity. Ponieważ bariera potencjału jest bardzo mała, więc w normalnych warunkach tylko neutrony poruszające się prawie stycznie do powierzchni są odbijane. Jednak neutrony UCN mają tak małą prędkość (poniżej 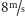), że od niektórych materiałów są odbijane niezależnie od kąta padania.

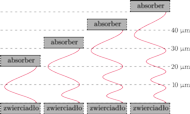
Rys. 1 Schemat przedstawiający kształt funkcji falowej dla pierwszych czterech wartości energii neutronu w studni potencjału grawitacyjnego.

Pułapka skonstruowana przez zespół Nesvizhevsky’ego może być formalnie opisana jako studnia potencjału. Cząstka jest uwięziona, ponieważ ma za mało energii, żeby pokonać przyciąganie grawitacyjne. Klasycznie cząstka może mieć w takiej sytuacji dowolną energię (tzn. jej energia zmienia się w sposób ciągły), dopóki jest ona mniejsza niż energia ucieczki. Ale w mechanice kwantowej cząstka w studni potencjału może zajmować tylko dyskretne poziomy energii. Opis matematyczny rozważanego problemu można znaleźć w artykule. Przewiduje on, że energia neutronu w pułapce przyjmuje dyskretne wartości numerowane główną liczbą kwantową 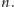Dla każdej energii tworzy się w studni fala stojąca, która ma maksimów. Oznacza to, że prawdopodobieństwo znalezienia neutronu na danej wysokości zmienia się tak, jak jest to pokazane na Rys. 1.

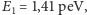
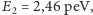
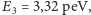
Pod wpływem grawitacji neutron oscyluje między brzegami studni utworzonej przez pole grawitacyjne Ziemi i poziome zwierciadło odbijające. Z obliczeń analitycznych wynika, że energia dla pierwszych czterech stanów kwantowych wynosi: 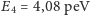( 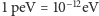). Natomiast klasyczna energia potrzebna do podniesienia neutronu o 10 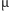m w polu grawitacyjnym o natężeniu g wynosi 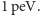Wynika stąd, że poziom 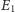odpowiada wysokości 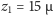m.

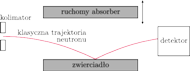
Rys. 2 Schemat doświadczenia [3]

Jak jednak sprawdzić, że w rzeczywistości jest tak, jak to przewiduje teoria? W doświadczeniu nie jest możliwe, żeby podnieść neutron, upuścić go i zmierzyć rozkład gęstości jako funkcję wysokości.

W doświadczeniu opisanym w publikacji [3] użyto poziomego zwierciadła długości 10 cm i neutronów o prędkościach około 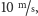uzyskanych z generatora ultra-zimnych neutronów w ILL w Grenoble. Schemat układu doświadczalnego jest pokazany na Rys. 2.

Oprócz zwierciadła użyto ruchomego absorbera neutronów – wielkość szczeliny między zwierciadłem i absorberem mogła być regulowana. W doświadczeniu neutrony przelatywały między zwierciadłem i absorberem. Rejestrowano liczbę  przechodzących przez układ neutronów w zależności od wielkości szczeliny między zwierciadłem i absorberem Spodziewano się, że jeżeli 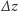będzie mniejsza niż szerokość odpowiadającą najmniejszemu stanowi kwantowemu, to 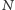powinno być równe zeru (neutrony w ogóle nie powinny docierać do detektora). Gdy szerokość 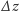zostanie powiększona do wielkości odpowiadającej pierwszemu stanowi kwantowemu, to powinien nastąpić gwałtowny wzrost liczby 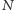 transmitowanych neutronów. Ogólnie oczekiwano skokowej zależności liczby  przechodzących przez układ neutronów od szerokości szczeliny

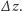
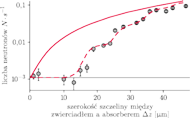
Rys. 3 Punkty oznaczone kółeczkami przedstawiają wyniki doświadczenia.

Wynik eksperymentu jest przedstawiony na Rys. 3.

Kolorowa linia ciągła oznacza krzywą teoretyczną przewidywaną przez fizykę klasyczną, natomiast kolorowa linia przerywana odpowiada przewidywaniom mechaniki kwantowej. Pozioma linia prosta wskazuje poziom sygnału przy wyłączonym źródle neutronów.

Jak widać, wyniki świetnie zgadzają się z kwantowo-mechnicznym opisem zjawiska. Dla małych wartości szerokości szczeliny sygnał w ogóle nie jest rejestrowany. Dopiero przy 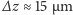liczba rejestrowanych neutronów zaczyna rosnąć w sposób skokowy, przy czym miejsca gwałtownych wzrostów zgadzają się z przewidywaniami mechaniki kwantowej.

Autorzy planują dalsze badania. Rozdzielczość energii jest określona przez zasadę nieoznaczoności i czas, jaki UCN spędzają w pułapce. Jeżeli ten czas będzie zwiększony, to można osiągnąć wyższą rozdzielczość. Silniejsze źródła UCN (budowane obecnie) pozwolą na uzyskanie dokładności umożliwiającej przeprowadzenie testów fundamentalnych praw fizyki.

Chodzi przede wszystkim o test zasady równoważności. Jest ona kluczowym krokiem prowadzącym do ogólnej teorii względności. Stwierdza, że efekty przyśpieszenia są nieodróżnialne od efektów jednorodnego pola grawitacyjnego. Oznacza to, że masa bezwładna i masa grawitacyjna neutronów są równoważne. Ten postulat trzeba sprawdzić doświadczalnie, a badania Nesvizhevsky’ego i jego kolegów idą w kierunku przeprowadzenia takiego testu o większej dokładności niż uzyskana innymi metodami.