Klub 44F - zadania I 2011»Zadanie 510
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44F - zadania I 2011
- Publikacja w Delcie: styczeń 2011
- Publikacja elektroniczna: 20 grudnia 2010
- Artykuł źródłowy w wersji do druku [application/pdf]: (65 KB)
Masa wolframowego włókna żarówki wynosi
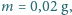 a ciepło
właściwe wolframu
a ciepło
właściwe wolframu
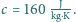 Gdy żarówka była zasilana
stałym napięciem 230 V, jej opór wynosił
Gdy żarówka była zasilana
stałym napięciem 230 V, jej opór wynosił
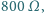 a temperatura
włókna była równa
a temperatura
włókna była równa
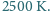 Podłączono tę żarówkę do napięcia
sinusoidalnie zmiennego o częstotliwości 50 Hz i wartości skutecznej 230 V.
Obliczyć przybliżoną głębokość modulacji promieniowania żarówki,
tzn. wielkość
Podłączono tę żarówkę do napięcia
sinusoidalnie zmiennego o częstotliwości 50 Hz i wartości skutecznej 230 V.
Obliczyć przybliżoną głębokość modulacji promieniowania żarówki,
tzn. wielkość
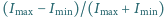 , gdzie
, gdzie
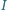 – moc
promieniowania. Założyć, że przepuszczalność szkła żarówki
nie zależy od długości fali.
– moc
promieniowania. Założyć, że przepuszczalność szkła żarówki
nie zależy od długości fali.
Można wykorzystać także następujące dane: gdy stałe napięcie zasilające
zmieniano w niewielkim zakresie i powoli, na każdy 1 wolt jego przyrostu
opór żarówki zwiększał się o
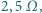 a temperatura włókna zwiększała
się o 0,7 K.
a temperatura włókna zwiększała
się o 0,7 K.

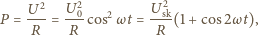
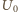 – amplituda napięcia,
– amplituda napięcia,
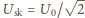 – wartość
skuteczna. Przyrównujemy zmienny składnik mocy do wyrażenia
– wartość
skuteczna. Przyrównujemy zmienny składnik mocy do wyrażenia
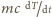 i znajdujemy amplitudę zmian temperatury równą
i znajdujemy amplitudę zmian temperatury równą
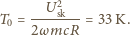
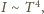 stwierdzamy, że szukana
głębokość modulacji wynosi
stwierdzamy, że szukana
głębokość modulacji wynosi
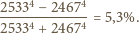
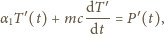
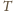 i
i
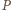 od ich
wartości średnich, natomiast
od ich
wartości średnich, natomiast
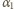 jest przyrostem mocy odprowadzanej
do otoczenia na jednostkę przyrostu temperatury. Przy wzroście napięcia o
jest przyrostem mocy odprowadzanej
do otoczenia na jednostkę przyrostu temperatury. Przy wzroście napięcia o
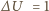 V przyrost tej mocy jest równy
V przyrost tej mocy jest równy
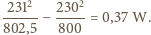 czyli liczbowa wartość
czyli liczbowa wartość
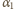 wynosi
wynosi
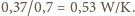 Ponadto
po prawej stronie równania należałoby wziąć pod uwagę zależność
Ponadto
po prawej stronie równania należałoby wziąć pod uwagę zależność
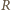 od temperatury w wyrażeniu
od temperatury w wyrażeniu
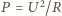 – jak można
wykazać, efekt ten jest równoważny dodaniu do
– jak można
wykazać, efekt ten jest równoważny dodaniu do
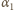 członu
członu
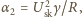 gdzie
gdzie
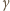 jest temperaturowym współczynnikiem
oporu. Wartość
jest temperaturowym współczynnikiem
oporu. Wartość
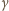 wynosi
wynosi
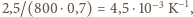 stąd
stąd
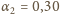 W/K. Dla uwzględnionego wcześniej wyrażenia
W/K. Dla uwzględnionego wcześniej wyrażenia
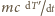 wielkością analogiczną jest
wielkością analogiczną jest
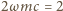 W/K, co oznacza,
że w pierwszym przybliżeniu można
W/K, co oznacza,
że w pierwszym przybliżeniu można
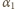 i
i
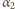 pominąć,
zwłaszcza że w dokładniejszym rozwiązaniu porównywane wielkości
wystąpiłyby w kwadracie.
pominąć,
zwłaszcza że w dokładniejszym rozwiązaniu porównywane wielkości
wystąpiłyby w kwadracie.