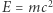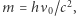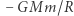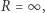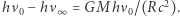O Słońcu i gwiazdach „kwantowych”
W XIX wieku - gdy tylko do światła Słońca i gwiazd zastosowano analizę widma płomieni, stało się jasne, że stanowią one kule gorącego gazu. Spróbujmy zatem opisać ich wnętrza...
Załóżmy zatem, że ciśnienie zmienia się z gęstością, jak w przemianie politropowej (opisanej w Delcie 10/2020):
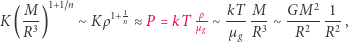 |
(1) |
gdzie kolorem wyróżniono równanie stanu gazu doskonałego; 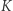 i
i 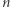 to stałe, a
to stałe, a 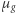 oznacza masę jednej cząsteczki. Jeśli więc gęstość to stosunek masy
oznacza masę jednej cząsteczki. Jeśli więc gęstość to stosunek masy 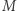 i objętości
i objętości 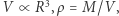 to
to 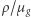 jest proporcjonalne do liczby moli na jednostkę objętości, jak w tradycyjnej postaci tego równania. Dla kulistej gwiazdy w grubym przybliżeniu
jest proporcjonalne do liczby moli na jednostkę objętości, jak w tradycyjnej postaci tego równania. Dla kulistej gwiazdy w grubym przybliżeniu 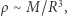 pomijając przy tym czynniki rzędu kilka (
pomijając przy tym czynniki rzędu kilka (  i inne). W tej samej konwencji pole przekroju kuli
i inne). W tej samej konwencji pole przekroju kuli 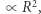 a w równowadze siła parcia jest rzędu siły grawitacji gwiazdy,
a w równowadze siła parcia jest rzędu siły grawitacji gwiazdy, 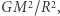 skąd wynika wzór na ciśnienie. Porównując skrajne wyrażenia, mamy
skąd wynika wzór na ciśnienie. Porównując skrajne wyrażenia, mamy
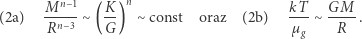 |
Zależność (2a) jest użyteczna i, co ważniejsze, weryfikowana w oparciu o obserwacje. Wynika z niej, że dla 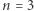 gwiazda o danej masie zachowując równowagę mechaniczną (hydrostatyczną), może przyjmować różne promienie. Oznacza to, że jej równowaga jest obojętna. Można także pokazać, że dla
gwiazda o danej masie zachowując równowagę mechaniczną (hydrostatyczną), może przyjmować różne promienie. Oznacza to, że jej równowaga jest obojętna. Można także pokazać, że dla 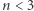 obiekty są w równowadze trwałej. Przykładem nie-gwiazdowym jest Ziemia o wnętrzu z ciekłych metali, gdzie gęstość praktycznie nie zmienia się z ciśnieniem (
obiekty są w równowadze trwałej. Przykładem nie-gwiazdowym jest Ziemia o wnętrzu z ciekłych metali, gdzie gęstość praktycznie nie zmienia się z ciśnieniem ( 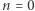 w równaniu 1). Dla
w równaniu 1). Dla 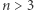 gwiazda nie jest stabilna i albo ulega rozproszeniu, albo kurczy się, aż zmiana własności sprasowanego gazu spowoduje, że
gwiazda nie jest stabilna i albo ulega rozproszeniu, albo kurczy się, aż zmiana własności sprasowanego gazu spowoduje, że 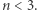
W praktyce w grupach podobnych gwiazd możemy spotkać dwie sytuacje: (a) dla każdej gwiazdy z osobna równanie politropy (1) jest dobrym przybliżeniem dla pewnego ustalonego 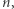 ale z różnymi wartościami
ale z różnymi wartościami 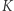 ; oraz (b) dla całej grupy
; oraz (b) dla całej grupy  i
i 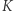 są ustalone. Przypadek (a) dotyczy gwiazd zbudowanych ze zwykłego gazu, w których transport ciepła na zewnątrz odbywa się dzięki konwekcji. Dla nas jest istotne, że elementy konwektywne poruszają się w czasie
są ustalone. Przypadek (a) dotyczy gwiazd zbudowanych ze zwykłego gazu, w których transport ciepła na zewnątrz odbywa się dzięki konwekcji. Dla nas jest istotne, że elementy konwektywne poruszają się w czasie 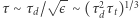 - gdzie
- gdzie 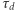 oznacza czas dynamiczny, a
oznacza czas dynamiczny, a 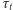 czas termiczny (szczegóły na marginesie), który jest znacznie krótszy niż czas termiczny
czas termiczny (szczegóły na marginesie), który jest znacznie krótszy niż czas termiczny 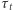 - wymieniając z otoczeniem znikomą część
- wymieniając z otoczeniem znikomą część  zapasu energii, czyli w dobrym przybliżeniu uczestniczą w przemianie adiabatycznej (mówimy zatem o konwekcji quasi-adiabatycznej).
zapasu energii, czyli w dobrym przybliżeniu uczestniczą w przemianie adiabatycznej (mówimy zatem o konwekcji quasi-adiabatycznej).
Przy temperaturach panujących w gwiazdach atomy są w pełni zjonizowane, tak że energia cieplna gazu pochodzi praktycznie wyłącznie z ruchu kinetycznego elektronów i jąder, a wtedy wykładnik adiabaty wynosi 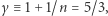 czyli
czyli 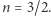 Takie modele politropowe dobrze opisują wnętrza gwiazd chemicznie jednorodnych, należących do tzw. ciągu głównego, jak np. Słońce o typie widmowym
Takie modele politropowe dobrze opisują wnętrza gwiazd chemicznie jednorodnych, należących do tzw. ciągu głównego, jak np. Słońce o typie widmowym 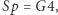 ale chłodniejszych niż
ale chłodniejszych niż 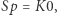 i o mniejszej masie, takich jak czerwone karły, w których konwekcja obejmuje praktycznie całą gwiazdę. Ponieważ dla chłodnych gwiazd obserwowana zależność masa-promień to
i o mniejszej masie, takich jak czerwone karły, w których konwekcja obejmuje praktycznie całą gwiazdę. Ponieważ dla chłodnych gwiazd obserwowana zależność masa-promień to 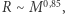 zatem z (2b)
zatem z (2b) 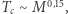 czyli dla coraz mniejszych mas temperatura w centrum spada. Dla masy
czyli dla coraz mniejszych mas temperatura w centrum spada. Dla masy 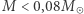 temperatura jest za niska do zapłonu reakcji jądrowych - takie gwiazdy to brązowe karły, świecące kosztem zmagazynowanej energii termicznej (ich
temperatura jest za niska do zapłonu reakcji jądrowych - takie gwiazdy to brązowe karły, świecące kosztem zmagazynowanej energii termicznej (ich 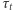 jest znacznie większe niż dla Słońca, zatem stygną bardzo długo). Podobną do nich politropową budowę mają licznie teraz odkrywane planety o masach większych od Jowisza. Natomiast podobnie do czerwonych olbrzymów, oprócz rozdętej politropowej otoczki konwektywnej, w samym centrum niczym pestka tkwi małe, ale bardzo gęste jądro (składające się z metalicznego wodoru w przypadku Jowiszów i zdegenerowanego helu - o czym później - w przypadku czerwonych olbrzymów).
jest znacznie większe niż dla Słońca, zatem stygną bardzo długo). Podobną do nich politropową budowę mają licznie teraz odkrywane planety o masach większych od Jowisza. Natomiast podobnie do czerwonych olbrzymów, oprócz rozdętej politropowej otoczki konwektywnej, w samym centrum niczym pestka tkwi małe, ale bardzo gęste jądro (składające się z metalicznego wodoru w przypadku Jowiszów i zdegenerowanego helu - o czym później - w przypadku czerwonych olbrzymów).
W znacznej części wnętrza Słońca do transportu energii zamiast konwekcji wystarcza promieniowanie, zatem zależność 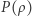 może być słabsza niż dla adiabaty,
może być słabsza niż dla adiabaty, 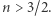 Budowę wnętrza Słońca możemy przybliżyć, zakładając jak Arthur Eddington, że stosunek ciśnienia gazu i ciśnienia promieniowania jest stały:
Budowę wnętrza Słońca możemy przybliżyć, zakładając jak Arthur Eddington, że stosunek ciśnienia gazu i ciśnienia promieniowania jest stały: 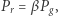 czyli
czyli 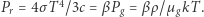 Stąd mamy
Stąd mamy 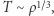 zatem całkowite ciśnienie to
zatem całkowite ciśnienie to 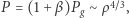 co odpowiada politropie
co odpowiada politropie 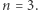 Przybliżenie jest niedoskonałe, bo wtedy Słońce byłoby niestabilne (w równowadze obojętnej, jak wynika z 2a). W rzeczywistości dzięki rosnącej ze spadkiem
Przybliżenie jest niedoskonałe, bo wtedy Słońce byłoby niestabilne (w równowadze obojętnej, jak wynika z 2a). W rzeczywistości dzięki rosnącej ze spadkiem 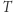 roli ciśnienia gazu średnie
roli ciśnienia gazu średnie 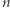 jest bliskie, ale mniejsze niż 3, więc na szczęście nasza najbliższa gwiazda prowadzi się dobrze.
jest bliskie, ale mniejsze niż 3, więc na szczęście nasza najbliższa gwiazda prowadzi się dobrze.
Gdy w podobnej do Słońca lub nieco bardziej masywnej gwieździe wyczerpie się w jądrze paliwo jądrowe (wodór) i zostanie hel, niezdatny do dalszej produkcji energii z powodu za niskiej temperatury, to parametr  opisujący jądro takiej gwiazdy rośnie od pierwotnej wartości 3/2 do nieskończoności, wyrównując temperaturę poprzez odprowadzenie energii na zewnątrz. Co oczywiste, już po zbliżeniu się do
opisujący jądro takiej gwiazdy rośnie od pierwotnej wartości 3/2 do nieskończoności, wyrównując temperaturę poprzez odprowadzenie energii na zewnątrz. Co oczywiste, już po zbliżeniu się do 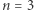 staje się ono niestabilne i pod naciskiem otoczki kurczy się, aż osiągnie
staje się ono niestabilne i pod naciskiem otoczki kurczy się, aż osiągnie 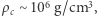 kiedy istotne stają się efekty kwantowe, o czym poniżej.
kiedy istotne stają się efekty kwantowe, o czym poniżej.
Spektakularną ilustracją przypadku (b) są białe karły, dla których 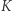 i
i  są z grubsza stałe. Postaramy się je wyznaczyć. Jak wiadomo, Syriusz A to najjaśniejsza gwiazda naszego nieba. Z precyzyjnych obserwacji jego pozycji wiadomo było, że wraz z towarzyszem - Syriuszem B - o podobnej masie, obiegają po orbitach wspólny środek ciężkości układu. Wobec małej jasności składnik B długo krył się w blasku składnika A. Gdy dzięki postępowi techniki udało się go zaobserwować, okazał się gorętszy (bardziej błękitny) niż Syriusz A, a zatem jego nikły blask można wyjaśnić tylko bardzo małym promieniem (nieco większym od Ziemi), co oznacza gęstość materii przekraczającą
są z grubsza stałe. Postaramy się je wyznaczyć. Jak wiadomo, Syriusz A to najjaśniejsza gwiazda naszego nieba. Z precyzyjnych obserwacji jego pozycji wiadomo było, że wraz z towarzyszem - Syriuszem B - o podobnej masie, obiegają po orbitach wspólny środek ciężkości układu. Wobec małej jasności składnik B długo krył się w blasku składnika A. Gdy dzięki postępowi techniki udało się go zaobserwować, okazał się gorętszy (bardziej błękitny) niż Syriusz A, a zatem jego nikły blask można wyjaśnić tylko bardzo małym promieniem (nieco większym od Ziemi), co oznacza gęstość materii przekraczającą 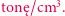
Siłę można zapisać jako zmianę pędu 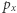 w czasie,
w czasie, 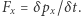 Zatem ciśnienie
Zatem ciśnienie 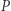 jako parcie
jako parcie 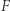 gazu na jednostkę powierzchni można zapisać jako strumień padającego/odbitego pędu (czynnik 2 pomijamy). Musimy jednak wziąć pod uwagę dwie możliwe prędkości elektronu, klasyczną
gazu na jednostkę powierzchni można zapisać jako strumień padającego/odbitego pędu (czynnik 2 pomijamy). Musimy jednak wziąć pod uwagę dwie możliwe prędkości elektronu, klasyczną 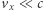 i relatywistyczną
i relatywistyczną 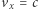 :
:
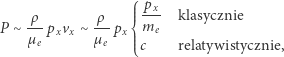 |
gdzie 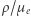 to liczba cząstek w jednostce objętości, a
to liczba cząstek w jednostce objętości, a 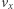 i
i 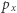 to ich prędkość i pęd, co daje strumień pędu na jednostkę powierzchni. Rozróżniamy tu masę gazu przypadającą na elektron -
to ich prędkość i pęd, co daje strumień pędu na jednostkę powierzchni. Rozróżniamy tu masę gazu przypadającą na elektron - 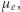 rzędu masy 2 protonów - od masy samego elektronu
rzędu masy 2 protonów - od masy samego elektronu 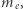 prawie 2000 razy mniejszej. Wraz ze wzorami z marginesu otrzymujemy
prawie 2000 razy mniejszej. Wraz ze wzorami z marginesu otrzymujemy
![⎧⎪ 32~3 h2 ρ 5~3 ⎪⎪⎪⎪ [------] ---(---) x ≪ 1 P ∼⎪⎪⎨ 20π 2~3 me µ e ⎪⎪ 31~3 ρ 4~3 ⎪⎪⎪⎪ [--1~3]hc (---) x ≫ 1, ⎪⎩ 8π µ e](/math/temat/astronomia/astrofizyka/2020/11/30/o-sloncu-i-gwiazdach-kwantowych/13x-80fe11ec7698cf216e451e302159d766a49abae1-dm-33,33,33-FF,FF,FF.gif) |
(2) |
gdzie 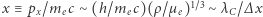 i
i 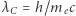 jest nazywana Comptonowską długością fali elektronu. Nawiasy kwadratowe zawierają czynniki pominięte w wyprowadzeniu, których dopisanie daje wynik ścisły. Dla krytycznej wartości
jest nazywana Comptonowską długością fali elektronu. Nawiasy kwadratowe zawierają czynniki pominięte w wyprowadzeniu, których dopisanie daje wynik ścisły. Dla krytycznej wartości 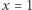 dostajemy gęstość, przy której można uznać, że elektrony są relatywistyczne:
dostajemy gęstość, przy której można uznać, że elektrony są relatywistyczne:
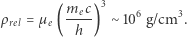 |
(3) |
Z powyższego wynika, że przy nierelatywistycznej degeneracji 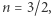 a więc białe karły winny spełniać zależność
a więc białe karły winny spełniać zależność 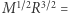 const. Masy wyznaczamy jak dla Syriusza B, z układów podwójnych. Natomiast promień białego karła można wyznaczyć z efektu poczerwienienia grawitacyjnego. W granicach błędów białe karły o masach
const. Masy wyznaczamy jak dla Syriusza B, z układów podwójnych. Natomiast promień białego karła można wyznaczyć z efektu poczerwienienia grawitacyjnego. W granicach błędów białe karły o masach 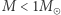 faktycznie spełniają powyższą zależność
faktycznie spełniają powyższą zależność 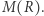 Pospolite białe karły mają
Pospolite białe karły mają 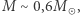 ale takie o
ale takie o 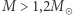 są spotykane.
są spotykane.
Fascynujący rezultat dostajemy także dla relatywistycznej degeneracji, czyli 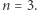 Wówczas
Wówczas 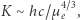 więc wzór (2a) zamienia się wprost we wzór na masę białego karła, zwaną masą Chandrasekhara:
więc wzór (2a) zamienia się wprost we wzór na masę białego karła, zwaną masą Chandrasekhara:
![⎡1~3⎤n~2 Ch=1√⎢⎢[3]hc(n+1)⎥⎥µ1. M 2π⎢⎣8π1~3µ4~3eG⎥⎦](/math/temat/astronomia/astrofizyka/2020/11/30/o-sloncu-i-gwiazdach-kwantowych/3x-b99fb8d9c3322fd8b314e73bb0c416176371c0c9-dm-33,33,33-FF,FF,FF.gif) |
(4) |
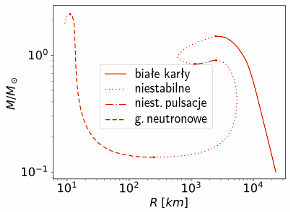
Realistyczna zależność masa-promień 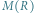 dla białych karłów i gwiazd neutronowych na podstawie rachunków warszawskiej grupy astrofizyki gwiazd neutronowych w CAMK (rysunek sporządzony przez Leszka Zdunika)
dla białych karłów i gwiazd neutronowych na podstawie rachunków warszawskiej grupy astrofizyki gwiazd neutronowych w CAMK (rysunek sporządzony przez Leszka Zdunika)
Na podstawie ścisłych wyprowadzeń w poprzednim artykule tej serii stałą proporcjonalności 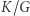 uzupełniłem o różne pomijane do tej pory czynniki. Wstawiając
uzupełniłem o różne pomijane do tej pory czynniki. Wstawiając 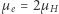 odpowiadające masywnemu białemu karłowi o składzie zdominowanym przez tlen i węgiel, otrzymujemy
odpowiadające masywnemu białemu karłowi o składzie zdominowanym przez tlen i węgiel, otrzymujemy 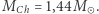 Masę całej gwiazdy można wyrazić przez stałe fizyczne, głównie atomowe! Nasz wynik oznacza, że biały karzeł nie może mieć masy większej niż
Masę całej gwiazdy można wyrazić przez stałe fizyczne, głównie atomowe! Nasz wynik oznacza, że biały karzeł nie może mieć masy większej niż 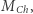 bo osiągając relatywistyczną degenerację, staje się niestabilny mechanicznie. Szczególnie spektakularny jest rezultat dla białego karła w układzie podwójnym, w którym towarzysz "na siłę" dostarcza mu materii, aż ten pierwszy osiągnie
bo osiągając relatywistyczną degenerację, staje się niestabilny mechanicznie. Szczególnie spektakularny jest rezultat dla białego karła w układzie podwójnym, w którym towarzysz "na siłę" dostarcza mu materii, aż ten pierwszy osiągnie 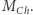 Taki nieszczęśnik zapada się wtedy pod własnym ciężarem, a dzięki uwolnionej energii grawitacyjnej i reakcjom jądrowym spektakularnie wybucha jako supernowa typu Ia: pod olbrzymim naciskiem jądra rozpadają się na nukleony, a pary proton-elektron łączą się w neutrony, które też są fermionami i podlegają zakazowi Pauliego.
Taki nieszczęśnik zapada się wtedy pod własnym ciężarem, a dzięki uwolnionej energii grawitacyjnej i reakcjom jądrowym spektakularnie wybucha jako supernowa typu Ia: pod olbrzymim naciskiem jądra rozpadają się na nukleony, a pary proton-elektron łączą się w neutrony, które też są fermionami i podlegają zakazowi Pauliego.
Gwiazdy dostatecznie gęste, by istotny stał się zakaz Pauliego w przypadku ciężkich fermionów, protonów i neutronów, to gwiazdy neutronowe. Są one kolejną, bardziej zwartą niż białe karły, rodziną gwiazd, co pokazuje rysunek na marginesie. Prosta zależność 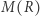 dla białych karłów świadczy o dobrym przybliżeniu przez politropę
dla białych karłów świadczy o dobrym przybliżeniu przez politropę 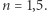 Jednak dla lekkich gwiazd neutronowych prawie płaski wykres świadczy o średnim
Jednak dla lekkich gwiazd neutronowych prawie płaski wykres świadczy o średnim  bliskim 3. W nich neutronizacja nie jest zupełna i wzrost gęstości prowadzi do zamiany dalszych atomów na neutrony, przy niewielkiej zmianie ciśnienia. Przypomina to kondensację pary w temperaturze
bliskim 3. W nich neutronizacja nie jest zupełna i wzrost gęstości prowadzi do zamiany dalszych atomów na neutrony, przy niewielkiej zmianie ciśnienia. Przypomina to kondensację pary w temperaturze 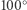 C, gdy ściskanie daje więcej cieczy, ale ciśnienie jest nadal ciśnieniem pary nasyconej. Z kolei dla mas ponad
C, gdy ściskanie daje więcej cieczy, ale ciśnienie jest nadal ciśnieniem pary nasyconej. Z kolei dla mas ponad 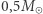 w centrum neutrony są tak ciasno upakowane, że zaczynają odpychać się siłami silnymi (jądrowymi), dominującymi nad ciśnieniem degeneracji, i
w centrum neutrony są tak ciasno upakowane, że zaczynają odpychać się siłami silnymi (jądrowymi), dominującymi nad ciśnieniem degeneracji, i 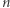 zbliża się do 1, a wykres staje się prawie pionowy. Maksymalna masa gwiazdy neutronowej wynosi, jak nam się obecnie wydaje, nieco powyżej
zbliża się do 1, a wykres staje się prawie pionowy. Maksymalna masa gwiazdy neutronowej wynosi, jak nam się obecnie wydaje, nieco powyżej 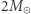 i jest skutkiem efektów silnego pola grawitacyjnego, wynikających z relatywistycznych poprawek do teorii grawitacji. Przy tej masie w gwieździe neutronowej powoduje ono niezaniedbywalne zakrzywienie czasoprzestrzeni, zgodnie z ogólną teorią względności. To zakrzywienie jest tylko kilka razy mniejsze niż w przypadku czarnej dziury. Czy pomiędzy rodziną gwiazd neutronowych a czarnymi dziurami istnieje trzecia rodzina zwartych gwiazd? Poszukiwania tak egzotycznych obiektów trwają.
i jest skutkiem efektów silnego pola grawitacyjnego, wynikających z relatywistycznych poprawek do teorii grawitacji. Przy tej masie w gwieździe neutronowej powoduje ono niezaniedbywalne zakrzywienie czasoprzestrzeni, zgodnie z ogólną teorią względności. To zakrzywienie jest tylko kilka razy mniejsze niż w przypadku czarnej dziury. Czy pomiędzy rodziną gwiazd neutronowych a czarnymi dziurami istnieje trzecia rodzina zwartych gwiazd? Poszukiwania tak egzotycznych obiektów trwają.
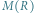
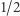
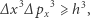
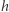
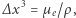
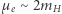
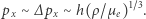
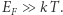
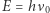 ), co na mocy relatywistycznego wzoru
), co na mocy relatywistycznego wzoru