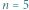Zaglądamy do środka gwiazdy
Znanym paradoksem jest, że o ile struktura Ziemi jest skomplikowana i do dziś słabo poznana, to wiemy, że gwiazdy są w pierwszym przybliżeniu "kulami gazowymi" - i tak właśnie zatytułował swoją książkę pierwszy badacz ich wnętrz, Robert Emden...
Przyjął on, że zmiany ciśnienia 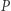 i gęstości
i gęstości 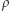 w funkcji odległości od środka
w funkcji odległości od środka  odbywają się przy zachowaniu relacji politropowej (politropowego równania stanu):
odbywają się przy zachowaniu relacji politropowej (politropowego równania stanu):
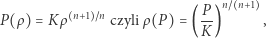 |
(1) |
gdzie 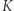 i
i  są stałymi, wynikającymi z własności materii danej gwiazdy; na przykład relatywistyczny gaz zdegenerowanych (ciasno upakowanych) elektronów jest dobrze opisany przez politropę z
są stałymi, wynikającymi z własności materii danej gwiazdy; na przykład relatywistyczny gaz zdegenerowanych (ciasno upakowanych) elektronów jest dobrze opisany przez politropę z 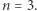 Póki co pominiemy dokładność tego przybliżenia w ogólnym przypadku i skupimy się na pokazaniu, jak w oparciu o nie można samemu skonstruować model gwiazdy, używając krótkiego programu komputerowego. Zacznijmy od znalezienia stosownych równań opisujących gwiazdę. Jeśli przez
Póki co pominiemy dokładność tego przybliżenia w ogólnym przypadku i skupimy się na pokazaniu, jak w oparciu o nie można samemu skonstruować model gwiazdy, używając krótkiego programu komputerowego. Zacznijmy od znalezienia stosownych równań opisujących gwiazdę. Jeśli przez 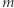 oznaczymy masę części gwiazdy zawartej w kuli o promieniu
oznaczymy masę części gwiazdy zawartej w kuli o promieniu 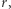 to powiększając ją o warstwę kulistą o grubości
to powiększając ją o warstwę kulistą o grubości 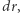 otrzymamy przyrost masy równy
otrzymamy przyrost masy równy 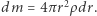 Przyspieszenie grawitacyjne na takiej powierzchni to
Przyspieszenie grawitacyjne na takiej powierzchni to 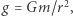 gdzie
gdzie 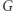 to stała grawitacji, ponieważ wpływ mas zewnętrznych znika zgodnie z twierdzeniem Newtona. Zatem korzystając ze szkolnego wzoru
to stała grawitacji, ponieważ wpływ mas zewnętrznych znika zgodnie z twierdzeniem Newtona. Zatem korzystając ze szkolnego wzoru 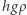 na ciśnienie atmosfery o gęstości
na ciśnienie atmosfery o gęstości 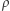 i grubości
i grubości 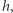 dostajemy w warstwie
dostajemy w warstwie 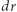 spadek ciśnienia hydrostatycznego
spadek ciśnienia hydrostatycznego
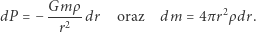 |
(2) |
Przed obliczeniami (patrz margines) pokażemy jeszcze, że wygodnie je wykonywać, wybierając pewne umowne jednostki oraz zmienne bezwymiarowe 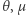 i
i 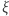 :
:
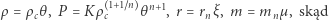 |
(3) |
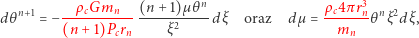 |
(4) |
gdzie 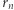 i
i 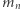 możemy zdefiniować, wymagając, by wyróżnione fragmenty wynosiły 1, i otrzymując
możemy zdefiniować, wymagając, by wyróżnione fragmenty wynosiły 1, i otrzymując
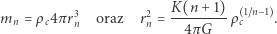 |
(5) |

Schemat blokowy działania metody RK(2)
W nowych zmiennych warunki początkowe w centrum sprowadzają się do 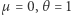 dla
dla 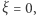 a ich przybliżenia dla małych
a ich przybliżenia dla małych 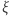 wynoszą
wynoszą
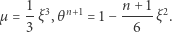 |
(6) |
Stąd i z (4) wynika, że teraz rozwiązania na 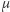 i
i 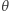 zależą tylko od
zależą tylko od 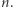 Rozwiązanie rozciąga się aż do powierzchni, gdzie dla
Rozwiązanie rozciąga się aż do powierzchni, gdzie dla 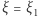 mamy
mamy 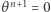 oraz
oraz 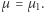
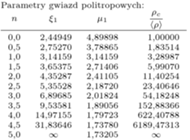
Do wykonania obliczeń można się posłużyć krótkim programem napisanym w języku python do ściągnięcia ze stron autora. Obliczenia wykonujemy, korzystając z równań (4), startując z wartości otrzymanych z (6). Program rysuje wykresy przebiegu ciśnienia i gęstości w gwieździe, przykład wykresu na następnej stronie. Zestawienie dokładnych wyników na powierzchni dla różnych  mieści tabela pod wykresem.
mieści tabela pod wykresem.
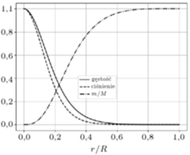
Wykres dla 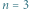
Dotąd nie korzystaliśmy z praw różniczkowania poza oczywistym 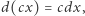 z warunkiem
z warunkiem 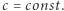 Analityczne rozwiązania równań Emdena istnieją dla trzech wartości
Analityczne rozwiązania równań Emdena istnieją dla trzech wartości 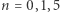 :
: 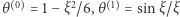 oraz
oraz 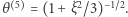 To ostatnie rozwiązanie jest graniczne:
To ostatnie rozwiązanie jest graniczne: 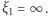 Dla
Dla 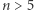 fizyczne rozwiązania nie istnieją, bo wykres
fizyczne rozwiązania nie istnieją, bo wykres 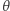 nie przecina osi
nie przecina osi 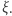 By sprawdzić te rozwiązania i wyrazić
By sprawdzić te rozwiązania i wyrazić 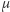 przez
przez 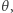 trzeba jednak skorzystać z prawa różniczkowania
trzeba jednak skorzystać z prawa różniczkowania 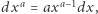 wynikającego z dwumianu Newtona
wynikającego z dwumianu Newtona 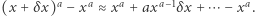 Użyjemy go tylko w tym akapicie i jego znajomość nie jest potrzebna w dalszej części. Wówczas lewa strona (4) przybiera postać
Użyjemy go tylko w tym akapicie i jego znajomość nie jest potrzebna w dalszej części. Wówczas lewa strona (4) przybiera postać 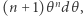 co po uproszczeniu po obu stronach daje rozwiązanie:
co po uproszczeniu po obu stronach daje rozwiązanie:
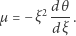 |
(7) |
Wynik dla 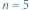 pochodzi z rozwiązania analitycznego
pochodzi z rozwiązania analitycznego
Mając z obliczeń 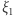 i
i 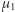 na powierzchni, rzeczywisty promień
na powierzchni, rzeczywisty promień 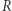 i masę gwiazdy
i masę gwiazdy 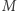 obliczamy z (3), otrzymując
obliczamy z (3), otrzymując 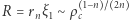 i
i 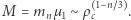 Eliminując
Eliminując 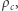 otrzymujemy:
otrzymujemy:
![n (n+1) Mn−1R3−n =-1-[ K-------] µ n−1 1ξ31−n= const. 4 π G](/math/temat/astronomia/astrofizyka/2020/09/30/zagladamy-do-srodka-gwiazdy/8x-d16fb480de535f0f17cafa5737228f31aa05d1c1-dm-33,33,33-FF,FF,FF.gif) |
(8) |
W podobny sposób średnia gęstość 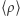 to
to 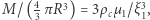 skąd przy pomocy (4)
skąd przy pomocy (4)
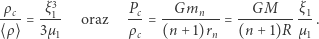 |
(9) |
Zależność 8 jest bardzo ważna i może być weryfikowana w oparciu o obserwacje astronomiczne. Odwracając problem, dla znanych 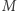 i
i 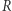 oraz
oraz 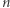 można obliczyć
można obliczyć 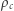 i
i 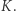
Z równania (8) wynika, że dla 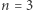 gwiazda o danej masie zachowując równowagę mechaniczną (hydrostatyczną), może przyjmować różne promienie. Oznacza to, że jej równowaga jest obojętna. Można pokazać, że w równowadze trwałej są kule gazowe dla
gwiazda o danej masie zachowując równowagę mechaniczną (hydrostatyczną), może przyjmować różne promienie. Oznacza to, że jej równowaga jest obojętna. Można pokazać, że w równowadze trwałej są kule gazowe dla 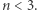 Przykładem jest Ziemia o wnętrzu złożonym z ciekłych metali, gdzie gęstość praktycznie nie zmienia się z ciśnieniem, co oznacza
Przykładem jest Ziemia o wnętrzu złożonym z ciekłych metali, gdzie gęstość praktycznie nie zmienia się z ciśnieniem, co oznacza 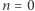 w równaniu (1). Natomiast dla
w równaniu (1). Natomiast dla 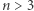 gwiazda nie jest trwała: ulega albo rozproszeniu, albo kurczy się do momentu, w którym zmiana własności sprasowanego gazu spowoduje
gwiazda nie jest trwała: ulega albo rozproszeniu, albo kurczy się do momentu, w którym zmiana własności sprasowanego gazu spowoduje 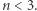
Używając równania (9), można także obliczyć temperaturę w centrum gwiazdy. Skorzystamy z równania stanu gazu doskonałego, zapisanego jako 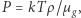 gdzie
gdzie 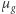 to masa cząsteczki gazu, a
to masa cząsteczki gazu, a 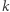 to stała Boltzmanna. Jeśli
to stała Boltzmanna. Jeśli 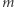 i
i 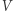 to masa i objętość gazu, to gęstość jest
to masa i objętość gazu, to gęstość jest 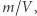 a stała liczba Avogadro
a stała liczba Avogadro 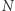 jest ilością cząsteczek w molu, to
jest ilością cząsteczek w molu, to 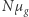 jest masą mola; zatem liczba moli to
jest masą mola; zatem liczba moli to 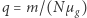 i stała gazowa jest równa
i stała gazowa jest równa 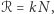 to podstawiając, otrzymujemy
to podstawiając, otrzymujemy 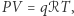 czyli zwykłą postać równania gazu. Wstawiając do (9), dostajemy
czyli zwykłą postać równania gazu. Wstawiając do (9), dostajemy
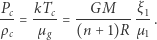 |
(10) |
Dla Słońca w przybliżeniu można użyć 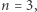 choć naprawdę
choć naprawdę  jest nieco mniejsze i zmienia się z promieniem. Wyjaśnienie, dlaczego tak się dzieje, to temat na inną opowieść: o porównaniu gwiazd zwykłych (takich jak Słońce) i "kwantowych", czyli białych karłów.
jest nieco mniejsze i zmienia się z promieniem. Wyjaśnienie, dlaczego tak się dzieje, to temat na inną opowieść: o porównaniu gwiazd zwykłych (takich jak Słońce) i "kwantowych", czyli białych karłów.