O liczbie układów podwójnych czarnych dziur i gwiazd neutronowych
Z obserwacji zespołów LIGO i Virgo, przez uchylone dopiero co okno "falowo-grawitacyjne" - w odróżnieniu od tradycyjnej astronomii korzystającej, z informacji pochodzących z okna elektromagnetycznego - wyłania się coraz wyraźniejszy obraz Wszechświata wypełnionego niewidzialnymi do tej pory układami podwójnymi czarnych dziur o różnych masach, układami podwójnymi gwiazd neutronowych, a także różnymi konfiguracjami układów mieszanych czarnej dziury i gwiazdy neutronowej.
I tak, okazuje się, że detektory sieci LIGO-Virgo najczęściej "słyszą" drgania czasoprzestrzeni pochodzące z masywnych układów podwójnych czarnych dziur (już kilkadziesiąt takich przypadków), a tylko od czasu do czasu te wytwarzane przez układy podwójne gwiazd neutronowych (do tej pory opublikowano wyniki dotyczące dwóch takich przypadków, sygnałów GW170817 i GW190425). Stosunek liczby detekcji układów podwójnych czarnych dziur (CD) do układów gwiazd neutronowych (GN) to 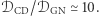
Jednocześnie szacowana z teorii ewolucji gwiazd częstość występowania bardzo ciasnych układów czarnych dziur i gwiazd neutronowych prowadzących do emisji fal grawitacyjnych rejestrowanych przez LIGO i Virgo wynosi około 10-100 Gpc 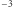 /rok dla układów podwójnych czarnych dziur oraz
/rok dla układów podwójnych czarnych dziur oraz 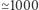 Gpc
Gpc 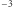 /rok dla układów podwójnych gwiazd neutronowych. Jak to więc możliwe, że na jednostkę czasu rejestruje się więcej układów podwójnych czarnych dziur, ale częstość występowania ich zderzeń w standardowej objętości jest dużo mniejsza?
/rok dla układów podwójnych gwiazd neutronowych. Jak to więc możliwe, że na jednostkę czasu rejestruje się więcej układów podwójnych czarnych dziur, ale częstość występowania ich zderzeń w standardowej objętości jest dużo mniejsza?
Załóżmy dla uproszczenia, że układy podwójne powstają podczas ewolucji zwykłych gwiazd (żargonowo "w polu gwiazdowym"); możliwe jest również dynamiczne tworzenie się układów podwójnych, gdy jeden obiekt znajdzie się tak blisko drugiego, że zostaną grawitacyjnie związane, jednak tego typu procesy są uważane za dużo mniej wydajne. Gwiazdy "pola" powstają w obszarach gwiazdotwórczych z pierwotnego gazu od razu w parach, po czym wspólnie ewoluują. Z obserwacji wynika, że większość gwiazd znajduje się w układach podwójnych lub wielokrotnych, a tempo ewolucji gwiazdy zależy od jej początkowej masy: im większa masa, tym szybsza ewolucja. Jednocześnie mało masywnych gwiazd jest dużo więcej niż bardzo masywnych. Liczba gwiazd o masie 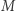 w przedziale mas
w przedziale mas 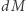 jest opisywana gęstością rozkładu prawdopodobieństwa. Dla kolejnego uproszczenia przyjmiemy pierwszą z brzegu (w istocie, historycznie pierwszą) funkcję rozkładu mas początkowych gwiazd
jest opisywana gęstością rozkładu prawdopodobieństwa. Dla kolejnego uproszczenia przyjmiemy pierwszą z brzegu (w istocie, historycznie pierwszą) funkcję rozkładu mas początkowych gwiazd 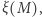 zaproponowaną w 1955 roku przez Edwina Salpetera:
zaproponowaną w 1955 roku przez Edwina Salpetera:
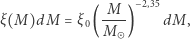 |
(1) |
gdzie 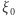 jest stałą związaną z lokalną gęstością gwiazd. Tempo powstawania gwiazd
jest stałą związaną z lokalną gęstością gwiazd. Tempo powstawania gwiazd 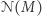 w danym przedziale mas w przeciętnej Galaktyce (na przykład takiej jak nasza) jest związane z funkcją rozkładu mas gwiazd,
w danym przedziale mas w przeciętnej Galaktyce (na przykład takiej jak nasza) jest związane z funkcją rozkładu mas gwiazd,
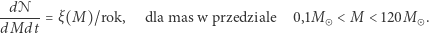 |
(2) |
Gwiazdy na początku swej ewolucji na ciągu głównym (to znaczy wtedy, gdy "spalają" w jądrze wodór, produkując hel), których masa początkowa jest większa niż pewna krytyczna wartość (około 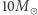 ), wybuchają w końcu jako supernowe, pozostawiając po sobie zwarte jądro: gwiazdę neutronową lub czarną dziurę. Na potrzeby dyskusji załóżmy, że gwiazdy o masach od 10 do
), wybuchają w końcu jako supernowe, pozostawiając po sobie zwarte jądro: gwiazdę neutronową lub czarną dziurę. Na potrzeby dyskusji załóżmy, że gwiazdy o masach od 10 do 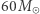 produkują gwiazdy neutronowe, a powyżej
produkują gwiazdy neutronowe, a powyżej 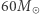 wyłącznie czarne dziury. W rzeczywistości sytuacja jest bardziej skomplikowana, ponieważ tempo i efekty ewolucji zależą nie tylko od masy, ale również od początkowego składu gwiazdy (zawartości pierwiastków cięższych od helu, czyli żargonowo "metaliczności"), tempa rotacji gwiazdy, wpływu towarzysza w układzie podwójnym i innych czynników. Niemniej jednak, porównując liczbę gwiazd produkujących czarne dziury i gwiazdy neutronowe,
wyłącznie czarne dziury. W rzeczywistości sytuacja jest bardziej skomplikowana, ponieważ tempo i efekty ewolucji zależą nie tylko od masy, ale również od początkowego składu gwiazdy (zawartości pierwiastków cięższych od helu, czyli żargonowo "metaliczności"), tempa rotacji gwiazdy, wpływu towarzysza w układzie podwójnym i innych czynników. Niemniej jednak, porównując liczbę gwiazd produkujących czarne dziury i gwiazdy neutronowe,
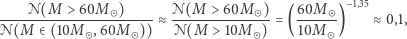 |
(3) |
dostajemy to, czego się spodziewaliśmy, to znaczy dużo mniejszą liczbę czarnych dziur w stosunku do liczby gwiazd neutronowych. Pomimo wielu różnic i złożoności procesu ewolucji stosunek częstości występowania układów podwójnych czarnych dziur 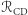 i układów podwójnych gwiazd neutronowych
i układów podwójnych gwiazd neutronowych 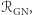 które emitują fale grawitacyjne wykrywane przez LIGO i Virgo, w pierwszym przybliżeniu wynosi tyle samo, co stosunek liczb układów podwójnych czarnych dziur i gwiazd neutronowych:
które emitują fale grawitacyjne wykrywane przez LIGO i Virgo, w pierwszym przybliżeniu wynosi tyle samo, co stosunek liczb układów podwójnych czarnych dziur i gwiazd neutronowych:
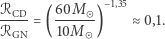 |
(4) |
Oczywiście szacowanie jest niedokładne, m.in. dlatego, że część układów może składać się z czarnej dziury i gwiazdy neutronowej, ale na nasze potrzeby "co do rzędu wielkości" jest wystarczające.
Do tej pory określaliśmy w przybliżeniu parametry całej populacji układów podwójnych, a teraz wykorzystamy je do porównania liczby rzeczywistych detekcji 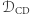 i
i 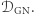 Niezbędnym elementem układanki jest określenie, jakie czynniki wpływają na "głośność" sygnału fal grawitacyjnych, a więc możliwość detekcji.
Niezbędnym elementem układanki jest określenie, jakie czynniki wpływają na "głośność" sygnału fal grawitacyjnych, a więc możliwość detekcji.
Amplituda fali 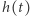 rejestrowana w momencie
rejestrowana w momencie 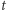 w detektorze jest praktycznie zawsze mniejsza od amplitudy szumu danych (sygnały są "schowane" w szumie detektora), więc by dokonać detekcji, sygnał jest zbierany przez
w detektorze jest praktycznie zawsze mniejsza od amplitudy szumu danych (sygnały są "schowane" w szumie detektora), więc by dokonać detekcji, sygnał jest zbierany przez 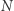 cykli fali. W praktyce korzysta się z metody filtru dopasowanego, to znaczy koreluje się dane z bankiem filtrów (modeli) sygnału, po czym wybiera najlepiej dopasowany, to znaczy taki z najwyższym stosunkiem sygnał-szum
cykli fali. W praktyce korzysta się z metody filtru dopasowanego, to znaczy koreluje się dane z bankiem filtrów (modeli) sygnału, po czym wybiera najlepiej dopasowany, to znaczy taki z najwyższym stosunkiem sygnał-szum 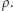 Innymi słowy, detektor gromadzi w czasie
Innymi słowy, detektor gromadzi w czasie 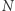 cykli moc sygnału ewoluującego w częstotliwości
cykli moc sygnału ewoluującego w częstotliwości 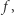 z odpowiednią fazą opisaną modelem sygnału. Liczba cykli
z odpowiednią fazą opisaną modelem sygnału. Liczba cykli 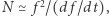 czyli wymiarowo
czyli wymiarowo 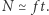 Na potrzeby naszego przybliżenia zdefiniujemy charakterystyczną amplitudę
Na potrzeby naszego przybliżenia zdefiniujemy charakterystyczną amplitudę 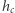 proporcjonalną do stosunku sygnał-szum
proporcjonalną do stosunku sygnał-szum 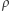 : energia to kwadrat amplitudy, czyli
: energia to kwadrat amplitudy, czyli 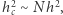 zatem
zatem 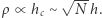 Z zależności
Z zależności 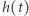 i
i 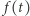 (patrz margines) wynika, że
(patrz margines) wynika, że 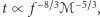 co oznacza
co oznacza
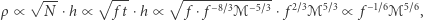 |
(5) |
z czego istotna jest dla nas zależność 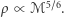 Stosunek sygnał-szum jest, tak jak amplituda sygnału, odwrotnie proporcjonalny do odległości do źródła. Zakładając minimalny
Stosunek sygnał-szum jest, tak jak amplituda sygnału, odwrotnie proporcjonalny do odległości do źródła. Zakładając minimalny 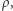 przy którym da się stwierdzić detekcję, definiujemy w ten sposób maksymalną odległość
przy którym da się stwierdzić detekcję, definiujemy w ten sposób maksymalną odległość 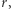 czyli maksymalną objętość
czyli maksymalną objętość 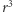 (zaniedbując efekty kosmologiczne i zakładając, że w dobrym przybliżeniu źródła są rozłożone równomiernie w przestrzeni). Ostatecznie do porównania liczby detekcji wchodzi
(zaniedbując efekty kosmologiczne i zakładając, że w dobrym przybliżeniu źródła są rozłożone równomiernie w przestrzeni). Ostatecznie do porównania liczby detekcji wchodzi 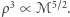 Stosunek liczby detekcji układów podwójnych czarnych dziur i układów gwiazd neutronowych - przyjmując, że przeciętna masa czarnej dziury to
Stosunek liczby detekcji układów podwójnych czarnych dziur i układów gwiazd neutronowych - przyjmując, że przeciętna masa czarnej dziury to 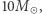 a gwiazdy neutronowej to
a gwiazdy neutronowej to 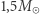 - jest więc następujący:
- jest więc następujący:
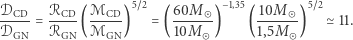 |
(6) |
Mimo że układów podwójnych czarnych dziur jest we Wszechświecie mniej, sygnały przez nie emitowane są silniejsze niż układów podwójnych gwiazd neutronowych (z powodu dużo większej masy ćwierku 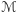 ), a zatem są "słyszalne" z dużo większej objętości i dlatego dominują w katalogach detekcji LIGO i Virgo.
), a zatem są "słyszalne" z dużo większej objętości i dlatego dominują w katalogach detekcji LIGO i Virgo.
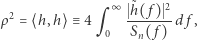
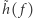 oznacza transformatę Fouriera
oznacza transformatę Fouriera 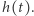
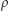 reprezentuje zsumowaną moc sygnału ważoną widmową (spektralną) gęstością mocy danych
reprezentuje zsumowaną moc sygnału ważoną widmową (spektralną) gęstością mocy danych