Co to jest?
Od obserwacji Eddingtona do obrazu czarnej dziury

W kwietniu 2019 roku mieliśmy okazję zobaczyć pierwszy obraz supermasywnej czarnej dziury w centrum galaktyki M87, zarejestrowany przez Teleskop Horyzontu Zdarzeń (Event Horizon Telescope, EHT). Obraz przedstawia niezbyt ostry jasny pierścień, czasem określany jako cień czarnej dziury. Szybko zrobił popkulturową karierę, zostając bohaterem licznych memów, ale czy aby wszyscy publikujący jego internetowe przeróbki wiedzą, co tak naprawdę przedstawia? Żeby to wyjaśnić, musimy najpierw cofnąć się w czasie o 100 lat, do początków teorii względności i teorii grawitacyjnego ugięcia promieni światła.
W roku 1915 Albert Einstein sformułował nową teorię grawitacji, ogólną teorię względności (OTW). Zamiast widzieć grawitację jako siłę oddziałującą między masywnymi ciałami zanurzonymi w trójwymiarowej przestrzeni euklidesowej, OTW opisuje ją jako krzywiznę czterowymiarowej rozmaitości - czasoprzestrzeni. Geometria czasoprzestrzeni determinuje tor ruchu fotonów, prowadząc do efektu ugięcia promieni światła w pobliżu masywnych obiektów. W świetle klasycznej newtonowskiej teorii grawitacji fotony, jako cząstki bezmasowe, nie oddziałują grawitacyjnie, a zatem ich trajektorie nie powinny ulegać zakrzywieniu. Jeśli jednak zapomnimy o tym na chwilę i założymy, że fotony poruszają się w polu grawitacyjnym tak jak dowolnie lekkie materialne cząstki, obliczymy kąt ugięcia światła 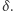 Zignorujemy również fakt, że taki ruch implikowałby, że fotony przyspieszają w polu grawitacyjnym, a więc prędkość światła musiałaby nie być stała. Same problemy! Dla małego kąta ugięcia
Zignorujemy również fakt, że taki ruch implikowałby, że fotony przyspieszają w polu grawitacyjnym, a więc prędkość światła musiałaby nie być stała. Same problemy! Dla małego kąta ugięcia 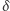 masywne fotony poruszałyby się po hiperbolach w newtonowskim polu grawitacyjnym. Przykład takiej trajektorii jest pokazany na rysunku na marginesie. Newtonowski kąt
masywne fotony poruszałyby się po hiperbolach w newtonowskim polu grawitacyjnym. Przykład takiej trajektorii jest pokazany na rysunku na marginesie. Newtonowski kąt 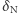 i odległość
i odległość 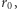 najmniejsza odległość między fotonem i centrum masy, są związane prostą formułą
najmniejsza odległość między fotonem i centrum masy, są związane prostą formułą
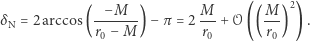 |
(*) |
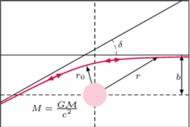
Grawitacyjne ugięcie promienia światła o kąt 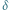 pod wpływem obiektu o masie
pod wpływem obiektu o masie 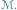 Strzałki na trajektorii zaznaczają, że foton może ją przebyć w obydwie strony
Strzałki na trajektorii zaznaczają, że foton może ją przebyć w obydwie strony
Wprowadziliśmy tu mierzoną w jednostkach odległości masę 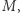 nazywaną też promieniem masowym. Jest ona związana ze standardową masą
nazywaną też promieniem masowym. Jest ona związana ze standardową masą 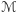 przez odpowiednie skalowanie,
przez odpowiednie skalowanie, 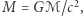 gdzie
gdzie 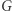 to stała grawitacji, natomiast
to stała grawitacji, natomiast  to prędkość światła w próżni.
to prędkość światła w próżni.
OTW rozwiązuje problem grawitacyjnego ugięcia trajektorii bezmasowego fotonu - to krzywizna czasoprzestrzeni spowodowana obecnością masywnego obiektu wymusza zmianę jego toru ruchu. W teorii względności fotony nie tylko pozostają bezmasowe, ale również zawsze poruszają się ze stałą prędkością 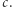 Einsteinowska formuła na obserwowany kąt
Einsteinowska formuła na obserwowany kąt 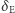 jest trochę bardziej zawiła i zadana przez całkę oznaczoną:
jest trochę bardziej zawiła i zadana przez całkę oznaczoną:
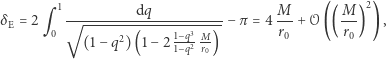 |
gdzie 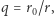 w tym przypadku
w tym przypadku 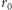 jest nie mniejsze od fizycznego promienia Słońca. Porównując te dwa równania, widzimy, że newtonowska formuła przewiduje dla małych wartości
jest nie mniejsze od fizycznego promienia Słońca. Porównując te dwa równania, widzimy, że newtonowska formuła przewiduje dla małych wartości 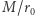 dwukrotnie mniejsze ugięcie
dwukrotnie mniejsze ugięcie 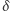 od formuły wynikającej z OTW - świetny test dla teorii względności! Dla Słońca
od formuły wynikającej z OTW - świetny test dla teorii względności! Dla Słońca 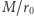 jest nie większe niż około
jest nie większe niż około 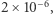 a zatem spokojnie możemy zaniedbać wyrazy wyższego rzędu. W 1919 roku ugięcie promieni światła odległych gwiazd przez grawitację Słońca zostało zaobserwowane i zmierzone po raz pierwszy podczas wyprawy badawczej pod kierownictwem sławnego brytyjskiego astronoma, Arthura Eddingtona. Wykorzystując całkowite zaćmienie Słońca, aby móc zarejestrować dokładne położenie gwiazd znajdujących się w pobliżu tarczy słonecznej, otrzymał on wynik
a zatem spokojnie możemy zaniedbać wyrazy wyższego rzędu. W 1919 roku ugięcie promieni światła odległych gwiazd przez grawitację Słońca zostało zaobserwowane i zmierzone po raz pierwszy podczas wyprawy badawczej pod kierownictwem sławnego brytyjskiego astronoma, Arthura Eddingtona. Wykorzystując całkowite zaćmienie Słońca, aby móc zarejestrować dokładne położenie gwiazd znajdujących się w pobliżu tarczy słonecznej, otrzymał on wynik 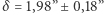 (sekundy łuku kątowego), który dość dobrze zgadzał się z wartością przewidzianą przez OTW,
(sekundy łuku kątowego), który dość dobrze zgadzał się z wartością przewidzianą przez OTW, 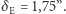 To bardzo niewielkie ugięcie promieni światła (rzędu tysięcznej części średnicy kątowej Księżyca w pełni) było pierwszym zweryfikowanym obserwacyjnie przewidywaniem OTW i wielkim triumfem Einsteina, który przyniósł mu światową sławę.
To bardzo niewielkie ugięcie promieni światła (rzędu tysięcznej części średnicy kątowej Księżyca w pełni) było pierwszym zweryfikowanym obserwacyjnie przewidywaniem OTW i wielkim triumfem Einsteina, który przyniósł mu światową sławę.

Innym nieoczywistym wnioskiem z teorii grawitacji Einsteina jest istnienie rozwiązań równań OTW, dla których krzywizna czasoprzestrzeni rośnie nieograniczenie, tworząc osobliwość. Jest ona otoczona horyzontem zdarzeń - sferą, którą można przekroczyć tylko w jednym kierunku. Rozwiązania te nazywamy czarnymi dziurami. Nic, nawet światło, przekraczając horyzont czarnej dziury, nie może już nigdy powrócić do zewnętrznego świata. Maksymalny kąt ugięcia promienia światła zależy od zwartości obiektu - obiekty o większej masie względem średnicy pozwalają na większą wartość 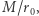 a zatem na większe ugięcie
a zatem na większe ugięcie 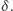 Czarne dziury są również pod tym względem bardzo szczególne, zapewniają bowiem maksymalną zwartość, a kąt ugięcia światła przez czarną dziurę może być… nieskończony! Dla wartości
Czarne dziury są również pod tym względem bardzo szczególne, zapewniają bowiem maksymalną zwartość, a kąt ugięcia światła przez czarną dziurę może być… nieskończony! Dla wartości 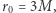 odpowiadającej parametrowi zderzenia
odpowiadającej parametrowi zderzenia 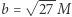 (patrz schemat na marginesie), wartość
(patrz schemat na marginesie), wartość 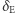 rośnie nieograniczenie, co odpowiada wielokrotnemu okrążeniu czarnej dziury przez foton. Jest to tak zwana orbita fotonowa. Dla mniejszych
rośnie nieograniczenie, co odpowiada wielokrotnemu okrążeniu czarnej dziury przez foton. Jest to tak zwana orbita fotonowa. Dla mniejszych 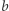 fotony wpadają pod horyzont zdarzeń, dla większych uciekają. Potężny teleskop może uchwycić te, którym udało się uciec, gdzieś daleko od czarnej dziury (
fotony wpadają pod horyzont zdarzeń, dla większych uciekają. Potężny teleskop może uchwycić te, którym udało się uciec, gdzieś daleko od czarnej dziury ( 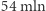 lat świetlnych w przypadku M87).
lat świetlnych w przypadku M87).
Z nowo zdobytą wiedzą możemy wrócić do obrazu M87. Poniższy rysunek przedstawia symulację obrazu czarnej dziury. Stworzenie tego rodzaju obrazu wymaga modelowania gorącej (miliardy kelwinów), turbulentnej plazmy opadającej na czarną dziurę i emitującej promieniowanie synchrotronowe.
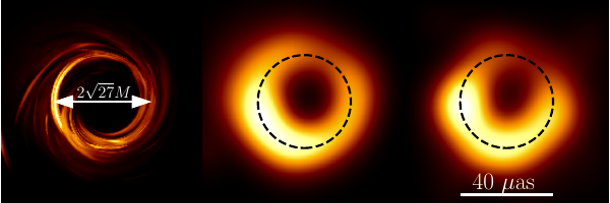
Z lewej: przykładowa klatka symulacji M87, zaznaczona średnica odpowiadająca 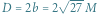 (autorzy: Wong, Prather i Gammie).
(autorzy: Wong, Prather i Gammie).
W środku: ta sama klatka rozmyta do rozdzielczości EHT, zaznaczony okrąg o promieniu 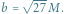
Z prawej: jeden z obrazów M87 uzyskany przez EHT z zaznaczonym wymiarem kątowym
Następnie trajektorie emitowanych fotonów trafiających do odległego obserwatora muszą być obliczone zgodnie z OTW, uwzględniając absorpcję i rozproszenie przez plazmę, i dopiero wtedy możemy z nich poskładać obraz taki jak na pierwszym panelu rysunku. Widzimy na nim pierścień o ciemnym wnętrzu - to sygnatura horyzontu zdarzeń, z którego wnętrza żaden foton nie może być wyemitowany. Ostry kontur pierścienia to fotony, które zbliżyły się do orbity fotonowej, a ich trajektorie zostały ugięte do wspomnianej krytycznej wartości parametru zderzenia 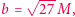 dając związek pomiędzy rozmiarem kątowym obrazu i masą czarnej dziury (po uwzględnieniu odległości między obserwatorem a źródłem, pozwalającej na konwersję między wymiarem liniowym i kątowym). Ale widzimy również dość chaotyczną spiralną strukturę dookoła ostrego konturu - to fotony emitowane przez dynamiczną, turbulentną plazmę wirującą wokół czarnej dziury. Fotony takie są emitowane blisko horyzontu zdarzeń, ale nie muszą być powiązane z orbitą fotonową. Niestety Teleskop Horyzontu Zdarzeń, chociaż chwali się największą rozdzielczością w historii naziemnych obserwacji astronomicznych, nie pozwala aktualnie na rozróżnienie tej subtelnej, złożonej struktury. Jeśli rozmyjemy symulowany obraz do efektywnej rozdzielczości EHT (ok. 20
dając związek pomiędzy rozmiarem kątowym obrazu i masą czarnej dziury (po uwzględnieniu odległości między obserwatorem a źródłem, pozwalającej na konwersję między wymiarem liniowym i kątowym). Ale widzimy również dość chaotyczną spiralną strukturę dookoła ostrego konturu - to fotony emitowane przez dynamiczną, turbulentną plazmę wirującą wokół czarnej dziury. Fotony takie są emitowane blisko horyzontu zdarzeń, ale nie muszą być powiązane z orbitą fotonową. Niestety Teleskop Horyzontu Zdarzeń, chociaż chwali się największą rozdzielczością w historii naziemnych obserwacji astronomicznych, nie pozwala aktualnie na rozróżnienie tej subtelnej, złożonej struktury. Jeśli rozmyjemy symulowany obraz do efektywnej rozdzielczości EHT (ok. 20 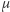 as - mikrosekund łuku kątowego, wystarczająco, by pozostając w Warszawie, poczytać New York Timesa leżącego na półce w nowojorskim sklepie z gazetami), otrzymamy obraz na środkowym panelu. Nareszcie przypomina to rezultat EHT! Wykorzystując duży zbiór tego rodzaju symulacji, pomiar masy czarnej dziury w M87 został odpowiednio skalibrowany, dając ostateczny wynik - ponad 6 miliardów mas Słońca.
as - mikrosekund łuku kątowego, wystarczająco, by pozostając w Warszawie, poczytać New York Timesa leżącego na półce w nowojorskim sklepie z gazetami), otrzymamy obraz na środkowym panelu. Nareszcie przypomina to rezultat EHT! Wykorzystując duży zbiór tego rodzaju symulacji, pomiar masy czarnej dziury w M87 został odpowiednio skalibrowany, dając ostateczny wynik - ponad 6 miliardów mas Słońca.
Pozostaje wyjaśnić, skąd bierze się asymetria pierścienia. Otóż jest to dobrze znana konsekwencja relatywistycznego efektu Dopplera. Rozgrzany gaz wiruje wokół czarnej dziury z ogromną prędkością, porównywalną z prędkością światła. Promieniowanie emitowane przez plazmę poruszającą się chwilowo w kierunku obserwatora jest wzmocnione, nieco podobnie jak dźwięk sygnału zbliżającego się do nas pociągu uzyskuje wyższą częstość, a więc i wyższą energię.
Równo 100 lat po obserwacji Eddingtona, mierzącego pojedyncze sekundy łuku odchylenia promieni światła, EHT pokazał obrazy, na których ugięcie jest setki tysięcy razy większe i powodowane przez obiekt miliardy razy bardziej masywny od Słońca. Wygląda jednak na to, że obydwa przypadki są bardzo dobrze opisane przez jedną i tę samą teorię, ogólną teorię względności, wciąż niezawodną po stuleciu obserwacyjnych i eksperymentalnych testów. Przyszłe usprawnienia EHT, w szczególności obserwacje w zakresie fal radiowych wyższej częstości, mogą pozwolić na oddzielenie turbulentnej składowej emisji od prostego, geometrycznego komponentu przewidzianego przez OTW, umożliwiając jeszcze dokładniejsze badania własności czarnych dziur, czasoprzestrzeni i poprawności teorii względności.
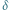 pod wpływem obiektu o masie
pod wpływem obiektu o masie 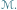 Strzałki na trajektorii zaznaczają, że foton może ją przebyć w obydwie strony
Strzałki na trajektorii zaznaczają, że foton może ją przebyć w obydwie strony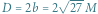 (autorzy: Wong, Prather i Gammie).
(autorzy: Wong, Prather i Gammie).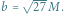
 w punkcie najmniejszej odległości
w punkcie najmniejszej odległości 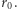 Alternatywna wersja, z prędkością
Alternatywna wersja, z prędkością  osiąganą w nieskończoności, daje taki sam kąt
osiąganą w nieskończoności, daje taki sam kąt 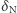 w pierwszym rzędzie rozwinięcia względem
w pierwszym rzędzie rozwinięcia względem 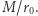
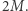
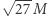 to wartość dla nierotującej czarnej dziury. Wraz z rotacją i kątem obserwacji kontur staje się nieco mniejszy i potencjalnie asymetryczny. Te efekty są jednak niewielkie wobec ograniczonej rozdzielczości EHT i niedokładności wyznaczonej odległości do M87.
to wartość dla nierotującej czarnej dziury. Wraz z rotacją i kątem obserwacji kontur staje się nieco mniejszy i potencjalnie asymetryczny. Te efekty są jednak niewielkie wobec ograniczonej rozdzielczości EHT i niedokładności wyznaczonej odległości do M87.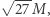 co jest związane z wpływem turbulentnej składowej obrazu.
co jest związane z wpływem turbulentnej składowej obrazu.