Rachunki się komplikują, gdy ciało spada z dużej wysokości. Tak dużej, że nie możemy już przyjąć, iż przyspieszenie ziemskie jest stałe. Na przykład z wysokości orbity Księżyca. Ponieważ przyspieszenie grawitacyjne maleje z kwadratem odległości, 384750 km od Ziemi (średnia odległość Księżyca od środka Ziemi) natężenie pola grawitacyjnego Ziemi jest około 3600 razy słabsze niż w pobliżu jej powierzchni. Wiedział to już Izaak Newton, co znacząco pomogło mu sformułować prawo powszechnej grawitacji.

Jak długo zatem będzie trwał spadek swobodny w centralnym polu grawitacyjnym Ziemi z wysokości orbity Księżyca? Promień orbity Księżyca jest 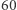razy większy od promienia Ziemi. Wobec takiej różnicy wielkości, dla uproszczenia, pomińmy w rachunkach rozmiar Ziemi. Dokładnie tak brzmiało jedno z zadań LX Olimpiady Astronomicznej. W każdym punkcie pionowej trajektorii znamy przyspieszenie ruchu, które jest przecież drugą pochodną położenia. Wystarczy zatem dwa razy scałkować... Niestety, nie jest to dobry pomysł na szybkie rachunki. Skoro jednak problem trafił do szkolnej olimpiady, musi być lepszy sposób rozwiązania.

Dzięki Keplerowi zadanie jest niemal trywialne. Jego III prawo mówi bowiem, że stosunek sześcianu wielkiej półosi orbity do kwadratu okresu obiegu planety wokół Słońca 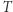jest jednakowy dla wszystkich planet: 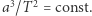Newton wykazał, że ta prosta reguła wynika z prawa powszechnego ciążenia i stosuje się do wszelkich orbit zamkniętych wokół ciała centralnego:

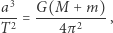gdzie 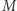i 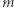to masy obiegających się ciał, a 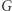jest stałą grawitacji. Dla orbity kołowej prawo to można łatwo wyprowadzić z zasad dynamiki Newtona i - oczywiście - prawa powszechnego ciążenia. Półoś 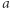sprowadza się w tym przypadku do promienia wodzącego łączącego oba ciała. Wzór powyższy pozostaje słuszny również dla orbit eliptycznych, ale jego wyprowadzenie jest nieco bardziej skomplikowane.

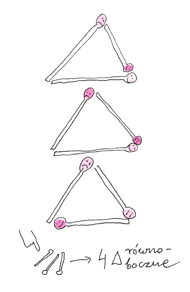
Suma mas obu ciał, 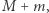w liczniku po prawej stronie w przypadku Słońca i planety nie jest oczywiście stała, gdyż masy planet różnią się bardzo, ale wszystkie są znacznie mniejsze od masy Słońca i z dobrym przybliżeniem masę 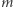planety można w powyższym wzorze pominąć. Jowisz jest wprawdzie 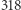razy masywniejszy od Ziemi, a blisko 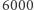razy od Merkurego, ale stanowi mniej niż jedną tysięczną masy Słońca. Tak więc III prawo jest spełnione dla wszystkich planet w Układzie Słonecznym z dokładnością do jednego promila.

Zastosujemy teraz to prawo do układów "Ziemia-Księżyc" i "Ziemia-ciało próbne", ale zanim "upuścimy" ciało próbne na Ziemię z orbity Księżyca, umieścimy je najpierw dokładnie na kołowej (w przybliżeniu) księżycowej orbicie wokół Ziemi:

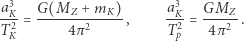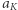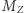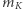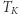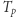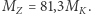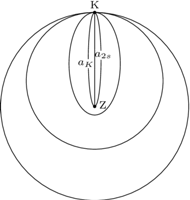
Teraz jest półosią wielką orbity Księżyca i ciała próbnego, i - masami Ziemi i Księżyca i odpowiednio i okresami obiegu Księżyca i ciała próbnego. Nie pominęliśmy masy Księżyca, gdyż nie jest ona znikoma w porównaniu z masą Ziemi: W efekcie ciało próbne będzie poruszać się nieco wolniej niż Księżyc i 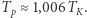Jeżeli umieścimy ciało próbne w odległości Księżyca od Ziemi, ale nadamy mu prędkość orbitalną mniejszą niż niezbędna, by utrzymało się na orbicie kołowej, to będzie się ono poruszało po orbicie eliptycznej. Im mniejsza będzie ta prędkość, tym elipsa orbity będzie bardziej spłaszczona. Przy pewnej prędkości ciało próbne uderzy w Ziemię. W naszym zadaniu tak się jednak nie stanie, gdyż pomijamy rozmiar Ziemi, czyli przyjmujemy, że ma dowolnie mały promień. W miarę dalszego zmniejszania prędkości początkowej w apogeum, to jest w punkcie najbardziej oddalonym od Ziemi, orbita ciała próbnego staje się coraz bardziej "smukła" i zbliża się do odcinka o długości 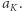Półoś orbity 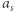w tak "zdegenerowanym" przypadku jest wobec tego dwa razy mniejsza: 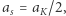a okres orbitalny 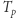jest równy podwojonemu czasowi spadku 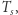którego szukamy: :

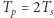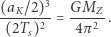Porównując odpowiednie wzory, otrzymujemy 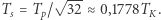W tablicach astronomicznych znajdujemy długość miesiąca syderycznego, czyli okres obiegu Księżyca wokół Ziemi 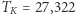dni, i ostatecznie otrzymujemy 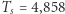dni 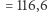godzin. Jest to około 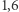razy dłużej niż czas podróży powrotnej z Księżyca astronautów programu Apollo.

Czytelnikowi pozostawiam obliczenie, ile minut wcześniej ciało próbne zderzy się z Ziemią, gdy nie pominiemy jej rozmiarów.

---