Zadania z matematyki - I 2020»Zadanie 1624
o zadaniu...
- Zadanie pochodzi z artykułu Zadania z matematyki - I 2020
- Publikacja w Delcie: styczeń 2020
- Publikacja elektroniczna: 31 sierpnia 2020
Znaleźć największą wartość sumy 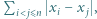 gdzie
gdzie ![x ∈[0,1] i](/math/temat/matematyka/analiza/zadania/2019/12/31/zm-1624/2x-7a859bc2426be6efd74caf08c9abc8e565add91b-im-2C,6B,73-FF,FF,FF.gif) dla
dla 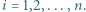
Znaleźć największą wartość sumy 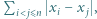 gdzie
gdzie ![x ∈[0,1] i](/math/temat/matematyka/analiza/zadania/2019/12/31/zm-1624/2x-7a859bc2426be6efd74caf08c9abc8e565add91b-im-2C,6B,73-FF,FF,FF.gif) dla
dla 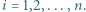
Zadanie 794 zaproponował pan Mikołaj Pater.
Dla liczb rzeczywistych 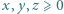 przyjmijmy:
przyjmijmy: 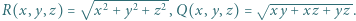 Wyznaczyć najmniejszą możliwą wartość wyrażenia
Wyznaczyć najmniejszą możliwą wartość wyrażenia
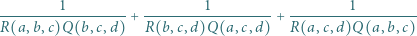 |
dla liczb 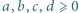 spełniających warunek
spełniających warunek 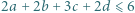 oraz wyznaczyć wszystkie czwórki
oraz wyznaczyć wszystkie czwórki 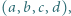 dla których to minimum jest osiągane.
dla których to minimum jest osiągane.
Udowodnić, że 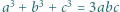 wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy 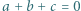 lub
lub 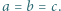
Liczby rzeczywiste 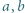 spełniają równość
spełniają równość 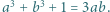 Wyznaczyć wszystkie możliwe wartości wyrażenia
Wyznaczyć wszystkie możliwe wartości wyrażenia 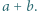
Liczby 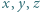 są rzeczywiste. Udowodnić, że jeśli
są rzeczywiste. Udowodnić, że jeśli
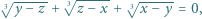 |
to pewne dwie z liczb 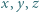 są równe.
są równe.
Udowodnić nierówność pomiędzy średnią geometryczną i arytmetyczną:
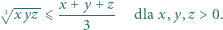 |
Wykazać, że liczba 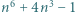 jest złożona dla każdej liczby całkowitej dodatniej
jest złożona dla każdej liczby całkowitej dodatniej 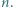
Wyznaczyć wszystkie trójki liczb rzeczywistych 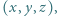 które spełniają równości
które spełniają równości
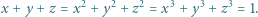 |
Liczby całkowite 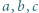 spełniają równość
spełniają równość
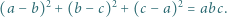 |
Dowieść, że 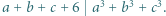
Liczby 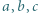 są całkowite. Wykazać, że jeśli liczba
są całkowite. Wykazać, że jeśli liczba 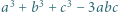 dzieli się przez 3, to dzieli się ona również przez 9.
dzieli się przez 3, to dzieli się ona również przez 9.
Udowodnić, że 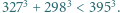 Uczynić to bez pomocy kalkulatora, wykonując przy tym możliwie najmniej rachunków.
Uczynić to bez pomocy kalkulatora, wykonując przy tym możliwie najmniej rachunków.
Dana jest liczba pierwsza 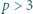 oraz takie liczby całkowite dodatnie
oraz takie liczby całkowite dodatnie 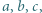 że
że
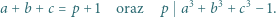 |
Dowieść, że co najmniej jedna z liczb 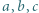 jest równa 1.
jest równa 1.
Różne liczby rzeczywiste 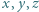 spełniają równość
spełniają równość
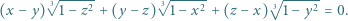 |
Dowieść, że 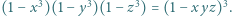
Liczby całkowite 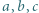 spełniają równość
spełniają równość
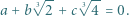 |
Udowodnić, że