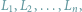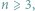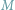Delta mi!

Podczas XXVII Kongresu Matematycznego, odbywającego się w Seulu między 13 a 21 sierpnia 2014 roku, prestiżową Nagrodę Nevanlinny (informatyczny odpowiednik Medalu Fieldsa) otrzymał pracujący w USA hinduski informatyk Subhash Khot. W laudacji poświęconej wynikom Khota jego mentor i współautor wielu prac, Sanjeev Arora, wspomniał o przełomowym wyniku uzyskanym przez profesora Uniwersytetu Warszawskiego, Krzysztofa Oleszkiewicza wraz z Elchananem Mosselem i Ryanem O'Donnellem...

Najbardziej zachęcającym aspektem uprawiania matematyki (oczywiście, poza niezaprzeczalnym pięknem matematycznych teorii) jest jej szeroka gama zastosowań i olbrzymia efektywność w modelowaniu świata rzeczywistego. Popularne jest nawet określenie "niepojęta skuteczność matematyki" (np. w pracy E. Wignera pod tożsamym tytułem The Unreasonable Effectiveness of Mathematics in the Natural Sciences). Warto jednak pamiętać, że modelowanie matematyczne jest czymś więcej niż tylko wyjątkowo użytecznym młotkiem wbijającym kolejne gwoździe, na których opiera się nasze zrozumienie wszechświata. Dzięki matematyce możemy modelować nie tylko to, co jest rzeczywiste (w jakimkolwiek tego słowa znaczeniu), ale też wszystko, co tylko potrafimy sobie wyobrazić.

Rozważmy przepływ nieściśliwego płynu w pewnym obszarze Załóżmy, że wiemy, jaka jest prędkość płynu w każdym punkcie obszaru, to znaczy że znamy pole prędkości, oznaczone w chwili początkowej Jak będzie wyglądało pole prędkości płynu w dowolnym momencie

Stado lwic gdzie oraz myśliwy (rozważani jako punkty płaszczyzny euklidesowej) poruszają się z równymi maksymalnymi prędkościami. Kiedy myśliwy ma skuteczną strategię ucieczki przed grupą lwic? Kiedy lwice mają skuteczną strategię pochwycenia myśliwego w skończonym czasie?

Żonglerka to starożytna sztuka, jej początki wydają się dorównywać wiekiem ludzkości, znane są np. rysunki żonglującej kobiety znalezione w egipskim grobowcu datowanym na XII wiek p.n.e. Wystarczy kilka kamieni i trochę praktyki, nie jest więc wcale zdumiewające, że ludzie zaczęli się tym zajmować bardzo dawno.

Jesteśmy świadkami szybkiego postępu w informatyce. Pojawiają się nowe języki programowania, biblioteki i platformy programistyczne. Korzystamy z obliczeń wielkiej skali, a swoje dane i aplikacje przenosimy do tzw. chmury. Jak jest możliwy tak szybki rozwój, pomimo dużego skomplikowania systemów komputerowych?

W artykule tym podejmiemy próbę wyjaśnienia nietypowej dysproporcji gatunkowej na kontynencie australijskim. Chodzi o niespotykany nigdzie indziej brak stałocieplnych drapieżników, przy jednoczesnym rozkwicie zimnokrwistych mięsożerców. Zwrócił na to uwagę w swoim artykule The case of missing meat eaters (opublikowanym w Natural History w 1993 roku) Tim Flannery, mammolog i paleontolog, specjalizujący się w australijskim ekosystemie.

Wydaje się, że nie ma rzeczy mniej logicznych niż uczucia. Czasami trwałe i szczęśliwe związki tworzą ludzie, o których mało kto by wcześniej powiedział, że są dla siebie stworzeni. Z drugiej strony, niejednokrotnie idealne, zdawałoby się, pary rozpadają się po pewnym czasie. W jaki sposób możemy więc przewidzieć dynamikę danego związku? Czy początkowy zachwyt drugą osobą będzie się umacniał, czy wręcz przeciwnie – zmieni się w niechęć? Na te pytania czasem trudno odpowiedzieć psychologom, a w zachowaniu partnerów niejednokrotnie trudno doszukać się logiki. Wydaje się, że angażowanie opartej na logice matematyki do tak trudnego i pozornie nieścisłego problemu jest skazane na porażkę. Okazuje się jednak, że „królowa nauk” nawet w takiej sytuacji jest w stanie wcisnąć swoje trzy grosze.

W Delcie 6/2011 artykuł Marii Donten-Bury o płaszczyźnie rzutowej został poprzedzony przedstawieniem sześciu jej (płaszczyzny, nie Marysi) postaci, pod jakimi daje się nam ona zaobserwować. Wobec tego, że postacie te są bardzo różnorodne, nasunąć się może wątpliwość, czy faktycznie wszystkie są wcieleniami tego samego matematycznego obiektu. Poniżej jest przedstawiony sposób, jak tę wątpliwość można rozstrzygnąć.

Obejrzeć płaszczyznę rzutową wcale nie jest łatwo. Z bliska, kiedy widzimy tylko mały fragment, wygląda całkiem jak zwykła płaszczyzna, więc to nic ciekawego. A gdybyśmy chcieli widzieć całą naraz, to musielibyśmy umieć widzieć w przestrzeni przynajmniej czterowymiarowej, bo w naszych trzech wymiarach po prostu nie da się jej porządnie ułożyć. Jeśli nie wierzysz, Czytelniku, wykonaj dający się wziąć w rękę, krawiecki model płaszczyzny rzutowej.

W matematyce, z jaką spotykamy się w szkole i na uniwersytecie, linię prostą identyfikuje się ze zbiorem punktów, w którym współrzędnymi są liczby rzeczywiste. Istnieje jednakże argument przeciw takiemu konkretnemu utożsamieniu, który opiera się na tym, iż nieskończenie wiele własności linii prostej nie może być ani dowiedzionych, ani obalonych za pomocą aksjomatów używanych w teorii mnogości (tzw. aksjomatów Zermelo–Fraenkla).