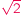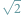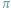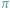Delta mi!

Rozważamy wielomian 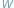o współczynnikach rzeczywistych stopnia 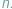Wiadomo, że wielomian taki ma 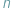pierwiastków zespolonych; niektóre z nich (czasami wszystkie) są, być może, rzeczywiste. Twierdzenie Sturma pozwala obliczyć liczbę pierwiastków rzeczywistych wielomianu 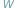należących do wybranego przedziału 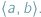Oczywiście, odpowiedź na to pytanie możemy uzyskać, stosując metodę badania funkcji wielomianowej 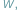znaną z analizy matematycznej. Metoda Sturma jest czysto algebraiczna, nie stosuje metod analizy matematycznej.

Liczby naturalne są niewątpliwie naturalne. Liczby całkowite niewątpliwie zasługują na nazwę całkowite. Liczby wymierne należałoby możne nazywać liczbami mierzącymi lub wymierzającymi, bowiem wszystkie pomiary wykonujemy w praktyce w liczbach wymiernych, zresztą nie tylko pomiary: wszelkie rachunki na konkretnych liczbach wykonywane są w praktyce wyłącznie w obrębie liczb wymiernych. Po co więc wprowadzać szersze, lecz znacznie trudniejsze pojęcie liczb rzeczywistych, skoro liczby wymierne wystarczają w rachunkach? Definicja liczb rzeczywistych nastręcza zawsze pewne trudności, wskutek tego w podręcznikach szkolnych jest raczej przemycana, niż precyzyjnie formułowana.

Poniższe zadania łączy to, że do rozwiązania każdego z nich można użyć pewnego Bardzo Znanego Twierdzenia, udowodnionego całkiem niedawno. Oczywiście to, że można strzelać z armaty do muchy nie oznacza, że zawsze trzeba...

W tym artykule ilustrujemy potęgę logarytmów w projektowaniu efektywnych algorytmów i obliczeń. Myślenie, w tle którego stoi logarytm, ukryty lub widoczny, nazwaliśmy myśleniem logarytmicznym. Stanowi ono jedną z podstawowych kompetencji niezbędnych przy efektywnym rozwiązywaniu rzeczywistych problemów informatycznych. Pokazujemy również - co może być ciekawe dla nauczycieli matematyki - jak wprowadzić pojęcie logarytmu, nie odwołując się do matematycznego formalizmu, a posługując się koncepcyjnym modelem redukcji rozmiaru problemu w każdym (lub w co drugim) kroku co najmniej o połowę. Może Cię zdziwić, że ta idea prowadząca do logarytmu występuje w algorytmie Euklidesa, który został opisany niemal 2000 lat przed wynalezieniem logarytmu przez Napiera.

Sztuka w trzech aktach z prologiem i epilogiem...

Punktem wyjścia niech będzie najsłynniejsza chyba matematyczna konstatacja, ta mianowicie, że liczba  jest niewymierna...

Matematyka, jak przystało na królową nauk, jest dyscypliną dość trudną i wymagającą umiejętności abstrakcyjnego myślenia. Jeżeli przyjąć za Galileuszem, że matematyka jest alfabetem, za pomocą którego Bóg opisał wszechświat, to trzeba przyznać, że jest to alfabet dość złożony i nie jest łatwo nauczyć się dobrze nim posługiwać. Jednym z jego ważniejszych elementów jest niewątpliwie nieskończoność.

W dowodzeniu nierówności często pomocna bywa tak zwana metoda stycznych. Zdarza się, że wykres funkcji leży nad pewną prostą styczną do niego lub pod taką prostą (wszędzie lub tylko na jakimś przedziale). To oznacza, że możemy oszacować wartości tej funkcji przez wartości funkcji liniowej, której wykresem jest wybrana styczna. Żeby takie oszacowanie doprowadziło do celu, wybrana styczna musi przechodzić przez punkt, dla którego badana nierówność jest równością. Przyjrzymy się kilku przykładom zastosowań tej metody.

Sprawdź, Czytelniku, czy potrafisz...

Gdy poznajemy matematykę, liczby oznaczane symbolami  oraz pojawiają się bardzo często. Uznając ważność tych liczb, badamy ich arytmetyczną naturę. Wiemy, że  jest liczbą niewymierną (L. Euler, 1737 r.) oraz  jest liczbą niewymierną (J.H. Lambert, 1767 r.). Przestępność liczby  wykazał Ch. Hermite w 1873 r., a przestępność liczby  wykazał w 1882 r. F. Lindemann. Wyznaczenie dobrych przybliżeń wartości tych liczb nie jest zadaniem banalnym. Przypomnijmy, jak można to zrobić.

W matematyce, z jaką spotykamy się w szkole i na uniwersytecie, linię prostą identyfikuje się ze zbiorem punktów, w którym współrzędnymi są liczby rzeczywiste. Istnieje jednakże argument przeciw takiemu konkretnemu utożsamieniu, który opiera się na tym, iż nieskończenie wiele własności linii prostej nie może być ani dowiedzionych, ani obalonych za pomocą aksjomatów używanych w teorii mnogości (tzw. aksjomatów Zermelo–Fraenkla).