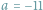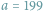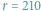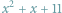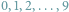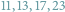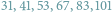Delta mi!

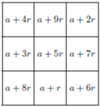
Kultura matematyczna jest kluczowym aspektem ogólnoludzkiej kultury. Wykazano, że wiele gatunków zwierząt (badano głównie ssaki i ptaki) potrafi liczyć, tzn. prawidłowo oceniać liczebność zbiorów skończonych. Oczywiście, precyzja takiej oceny maleje wraz z tą liczebnością (np. przeciętni ludzie radzą sobie z takim liczeniem do około siedmiu).

Jeśli się weźmie do ręki jajo i ściśnie palcami za „ostry” i „tępy” czubek, wyczuje się opór. Jest on dość spory, jak na niewielką grubość skorupki jaja. Przeciętne jajo wytrzymuje bez pękania nacisk odpowiadający ciężarowi dwuipółkilogramowego ciała. Udaje się dzięki temu prosta sztuczka, która spodobać się może wszystkim, którzy marzą o innym zastosowaniu nabiału niż produkcja wielojajecznych bab, serników i sękaczy na święta...

Piłki tenisowe na ogół pakowane są w rurkę po kilka sztuk. Wyobraźmy sobie piłki tak cenne, że pakowane są każda oddzielnie. Takie opakowanie to z matematycznego punktu widzenia walec...

W prezencie od znajomych dostałem zegar (rys. 1). Powiesiłem go sobie na ścianie i zacząłem wymyślać... inne zegary.

Materiały porowate robią coraz większą karierę. Jednym z bardziej popularnych haseł jest MOF (Metal-Organic Framework), czyli struktura(y) metaliczno-organiczna. Wiele zespołów zajmuje się twórczością w tej dziedzinie. Dosłownie. Tworzone są nowe materiały z nadzieją uzyskania filtrów, schowków na wodór, ditlenek węgla, radon.

Została popełniona oryginalna publikacja. Autorzy przekonują w niej, że kinematograficzna prezentacja wyników jest metodą naukową.

Od dłuższego czasu słyszymy o wspaniałej przyszłości komputerów kwantowych, a i naszej przy okazji. Sytuacja wydaje się podobna do fuzji termojądrowej, która od pół wieku za pół wieku ma rozwiązać nasze problemy energetyczne.

Wraz z wynalezieniem meta-materiałów o ujemnym współczynniku załamania ukrywanie się pod czapką-niewidką (a raczej peleryną-niewidką) z bajek, fantastyki czy magii przechodzi do rzeczywistości. Żyjemy jednak w czasoprzestrzeni, więc można pomyśleć o ukryciu się również w czasie, a nie tylko w przestrzeni. Chodziłoby np. o ukrycie procesu przesyłania (przetwarzania) informacji. Jak można by było to zrealizować?

Jest taki zdumiewający moment w dziejach świata, gdy my, ludzie, uznaliśmy za niezbędne udzielenie odpowiedzi na pytanie, co właściwie wyróżnia nas spośród wszelkich żywych stworzeń. Było to w wieku  VI. Owa niezbędność pojawiła się we wszystkich stronach świata, we wszystkich kulturach i – co jeszcze dziwniejsze, wobec braku możliwości bezpośredniego, a choćby nawet sensownie szybkiego kontaktu – pojawiła się jednocześnie.

Numer Delty poświęcony paradoksom nie byłby kompletny, gdyby nie pojawiła się w nim paradoksalna gra. Przyjrzyjmy się zatem pewnej grze, inspirowanej paradoksami teoriomnogościowymi, które rozkwitły w początkach XX wieku.

Amatorskie obserwacje można z powodzeniem wykonywać, nie przejmując się zanadto skomplikowaną aparaturą – do oszacowania rozmiarów kątowych oraz odległości pomiędzy obiektami na sferze niebieskiej wystarczy sprawna dłoń.

Sprawdź, Czytelniku, czy potrafisz...

Zamieszczony w poprzednim numerze, jako zapowiedź tego numeru, widoczny obok kwadrat magiczny jest dla  (lub ) i   złożony z samych liczb pierwszych.

W Delcie 3/1979 zamieściliśmy największy znany wówczas kwadrat magiczny złożony z różnych liczb pierwszych – było ich 169. Co więcej, był to kwadrat „cebulkowy”. A dziś – proszę: istnieje już „cebulkowy” kwadrat magiczny aż o trzy większy, złożony zatem z dwustu pięćdziesięciu sześciu liczb pierwszych. I jak tu nie wierzyć w postęp!

Sophie Germain (1776–1831), wbrew ówczesnym obyczajom matematyk, fizyk, metalurg i autorka ciekawych szkiców o kulturze, prawie na każdym kroku musiała udowadniać swą wiedzę i bronić swych dokonań przed rzeszami niedowiarków.

Załóżmy, że suma kw adratów trzech liczb naturalnych jest podwojonym kwadratem pewnej liczby naturalnej. Czy możliwe jest, żeby wówczas suma czwartych potęg tych trzech liczb była podwojoną czwartą potęgą tej samej liczby?

Wbrew oczywistemu skojarzeniu nie chodzi tu o Konrada Wallenroda, lecz o układankę, jaką przed wiekami wymyślili litewscy drwale...

Jeśli chcemy rozwiązać układ równań – taki zwykły, dwa równania liniowe z dwiema niewiadomymi – za pomocą komputera, całkiem wygodnie jest użyć metody wyznaczników...

...dwaj najmłodsi uczniowie Galileusza, Bonaventura Cavalieri i Evangelista Torricelli, byli ludźmi do tego stopnia pogodnymi i pełnymi poczucia humoru, że nawet podczas pracy naukowej robili sobie wzajemnie zaawansowane psikusy ku uciesze znajomych.

Zanim coś połkniemy, warto sprawdzić, czy aby to coś nie jest większe od nas...

Myślę, że niemal każdy Czytelnik miał okazję się z nią spotkać. Załóżmy, że mamy dany trójkąt, i wybierzmy dowolny punkt  z okręgu na nim opisanego. Wówczas rzuty prostokątne punktu  na proste zawierające boki danego trójkąta leżą na jednej prostej zwanej prostą Simsona.

Alfametycznych kwadratów poszukuję od ponad trzydziestu lat. Tylko dwa z nich dotąd opublikowałem (p. poniżej). Oba przykłady kwadratów słów trzyliterowych są ilustracją tzw. liczb automorficznych.

Czarna dziura, zgodnie z nazwą, jest pułapką, do której wszystko może wpaść, a nic nie może wylecieć – przynajmniej tak tę sprawę widzimy obecnie...

Od dość dawna wiadomo było, że peryhelium Merkurego nie zachowuje stałej orientacji względem Słońca, lecz obiega je w tempie 573” na wiek. Zjawisko to nie miałoby prawa wystąpić, gdyby Merkury był jedyną planetą Układu Słonecznego.

Wszystkie normalne gwiazdy mają dość zbliżony skład chemiczny, dlatego o wyglądzie ich widm decyduje temperatura powierzchniowa...

Ponad sto lat badań nad rozszerzalnością cieplną ciał dzieli pierwszy termoskop Galileusza z roku 1592 od termometru rtęciowego skonstruowanego przez Fahrenheita około roku 1715. W tym czasie nauczono się dokładnie porównywać temperatury ciał odkrywając „po drodze” anomalną rozszerzalność termiczną wody, a także obalając starożytne jeszcze przekonanie, że nasze ciało jest chłodniejsze w nocy niż we dnie (Santorio, przed 1634 rokiem).

Jeżeli dwa punkty materialne mają rozbiegnąć się do nieskończoności, to ich całkowita energia mierzona w układzie środka masy (tj. suma ich energii kinetycznych i wzajemnej grawitacyjnej) musi być równa zeru lub dodatnia. Podobnie, jeżeli biegną ku sobie z nieskończoności, to ich energia jest nieujemna, tory są krzywymi otwartymi, a więc ciała te spotkać się mogą tylko raz. Jest więc wykluczone złapanie się takich dwóch punktów materialnych na orbity zamknięte.

Kanały na Marsie odkrył w roku 1877 Giovanni Virginio Schiaparelli. Z oczywistych powodów wywołało to ogromne zainteresowanie.

Są dwa systemy wykładania astronomii: w jednym zaczyna się od obiektów najbliższych i zjawisk najłatwiej widocznych, w drugim zaczyna się od Wszechświata całą resztę traktując jako jego fragmenty. Dominuje system pierwszy...

Ciała doskonale czarnego (c.d.cz.) nie ma. Każde bowiem ciało w jakimś stopniu odbija padające na nie promieniowanie, natomiast według definicji, c.d.cz. niezależnie od swojej temperatury, powinno całkowicie pochłaniać padające na nie promieniowanie i to bez względu na jego skład widmowy. Dlaczego więc posługujemy się tym pojęciem?

W mechanice często posługujemy się pojęciem punktu materialnego. Rozważając ruch ciała redukujemy je do punktu obdarzonego masą. Ma to proste uzasadnienie w stosunku do gwiazd na niebie i ich ruchów obserwowanych z Ziemi; rozmiary gwiazd są zaniedbywalne w stosunku do ogromnej odległości, jaka nas od nich dzieli. Gorzej jest, gdy zastępujemy punktem piłkę, siekierę lub samochód. Czy ma to jakieś uzasadnienie?

Jeśli liczba naturalna jest największą liczbą pierwszą, to...

Zwykłe siodło do konnej jazdy ma dwa łęki i dwie klapy – z przodu i z tyłu jest podniesione do góry, z obu boków opada w dół. Jest przy tym wszędzie krzywe, czyli niepłaskie...

Także w świecie komputerów posługujemy się różnymi miarami. Podstawową jednostką mierzącą ilość danych jest bajt (B).

Joseph Louis Lagrange (1736--1813) był ogromnie zniesmaczony ciągle nieudanymi próbami ścisłego zdefiniowania koniecznego dla zastosowań matematyki pojęcia pochodnej funkcji. Rzecz udawała się właściwie tylko dla wielomianów.

Prawie dwieście lat temu Augustin Cauchy udowodnił, że wielościan wypukły, który ma sztywne ściany, jest cały sztywny, choćby jego krawędzie były wyposażone w najlepsze zawiasy. I postawił problem, czy założenie wypukłości jest konieczne.

Martin Gardner opisał pewną sztuczkę, która wygląda niewiarygodnie...

Oto spektakularne wyniki z lat 1997–2009, dotyczące liczb pierwszych.

Gdy do wielomianu podstawiać będziemy kolejno liczby , otrzymamy , – same liczby pierwsze. Reguła czy przypadek?