Delta mi!

Niniejszy odcinek Deltoidu o okrągłym (w systemie jedenastkowym) numerze jest odcinkiem ostatnim. Nie kryjemy smutku z tego powodu, cieszymy się jednocześnie, że na naszych łamach ta wspaniała seria ukazywała się przez okrągłych 10 lat. Mamy nadzieję, że jeszcze wiele razy nazwisko Autorki zagości w naszym spisie treści.
Joasiu, za Twoją nienaganną punktualność w dostarczaniu materiałów, zegarmistrzowską dokładność przy ich korekcie, a przede wszystkim za deltoidową fantastyczność serdecznie dziękujemy!

Redakcja

Większości problemów otwartych współczesnej matematyki nie da się zrozumieć bez zaawansowanej wiedzy, ale zdarzają się też takie, których sformułowania są zupełnie elementarne. Poniższa seria zadań prowadzi do jednego z nich.

Podzielmy kostkę na 27 przystających sześcianów (jak w kostce Rubika), a następnie wyrzućmy 7 z nich: ten ze środka oraz środkowy na każdej ze ścian. W kolejnych krokach konstrukcji powtarzajmy powyższą operację dla każdego z pozostających mniejszych sześcianów.

Na wiele problemów matematycznych warto spojrzeć z innej strony (lub z dwóch stron jednocześnie), przeanalizować dualną sytuację, dostrzec alternatywną wersję tego samego zagadnienia...

Zasada szufladkowa Dirichleta głosi, iż jeśli rozmieszczamy pewną liczbę obiektów w mniejszej liczbie szufladek, to któreś dwa z nich trafią do tej samej szufladki. Podobnie, jeśli liczba obiektów jest większa niż dwukrotność liczby szufladek, któreś trzy trafią razem do szufladki itd.

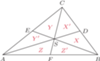
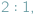Środkowa trójkąta to odcinek łączący wierzchołek ze środkiem przeciwległego boku. Środkowe przecinają się w jednym punkcie, zwanym środkiem ciężkości i dzieli on każdą z nich w stosunku licząc od wierzchołka trójkąta (rys. obok).

Zagadnienia związane z prawdopodobieństwem i statystyką bywają zaskakujące i nieintuicyjne. Zdarza się też często, że okazują się one znacznie łatwiejsze niż się na pierwszy rzut oka wydaje.

Tym razem o paraboli...

...medal - dwie strony, czego nie ma tu, musi być tam, a co weszło, musi wyjść.

Wysokością czworokąta nazwijmy prostą przechodzącą przez środek jego boku i prostopadłą do boku przeciwległego. W niektórych czworokątach wszystkie cztery wysokości przecinają się w jednym punkcie - ortocentrum czworokąta. Przykładowo kwadrat ma ortocentrum, a romb niebędący kwadratem nie ma.

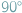W wielu zadaniach, w których występują kąty lub ich sumy, przydatne bywa przeniesienie pewnych figur tak, by kąty te znalazły się obok siebie. Szczególnie wygodne jest to wtedy, gdy suma pewnych kątów równa jest np. lub 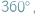a także, gdy niektóre z danych odcinków są równej długości.

Gra Black rozgrywana jest przez dwóch graczy (I - rozpoczynającego i II) na prostokątnej planszy podzielonej na kwadratowe pola jednostkowe; każdy z wymiarów planszy jest większy od 2...

Czasem warto przetłumaczyć problem na inny język, aby łatwiej go rozwiązać.

Oto kilka zadań związanych z istnieniem i własnościami pewnych krzywych lub łamanych na płaszczyźnie i w przestrzeni trójwymiarowej.

Prezentujemy kilka zadań wraz z "rozwiązaniami" i... lepszymi rozwiązaniami...

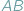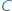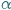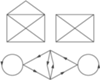
Odcinek widać z punktu pod kątem , gdy 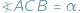Z twierdzenia o kątach wpisanych wynika, że jeśli punkty 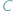i 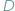leżą na okręgu po tej samej stronie jego cięciwy 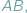to widać ją z i pod tym samym kątem (Rys. 1).

Fakt (*). W trójkącie prostokątnym środek przeciwprostokątnej jest równo odległy od wierzchołków. Również na odwrót, jeśli środek okręgu opisanego leży na boku trójkąta, to trójkąt ten jest prostokątny.

Farmer ma wilka, kozę, kapustę, łódkę i... coś do zrobienia.

Jeśli chcemy wyznaczyć długość pewnej krzywej lub łamanej, często warto ją rozwinąć albo w inny sposób rozprostować.

W dowolnym trójkącie odcinek łączący środki dwóch boków jest równoległy do trzeciego boku i dwukrotnie od niego krótszy. Ten prosty fakt okazuje się zadziwiająco przydatny.

Tym razem będziemy wycinać...

Styczniowy deltoid poświęcony był dwubarwnym mapom...

Które z rysunków 1 (a), (b), (c) da się narysować bez odrywania ołówka od kartki i bez rysowania ponownie wzdłuż narysowanej już linii?

Słynne twierdzenie orzeka, że każdą mapę da się pomalować najwyżej czterema barwami. Oczywiście, zawsze należy malować tak, by sąsiadujące ze sobą państwa miały różne kolory. Są jednak mapy, dla których wystarczy mniej barw.

Wiele zadań przestrzennych łatwiej rozwiązać, gdy najpierw zbada się analogiczny problem płaski. Taki dwuwymiarowy odpowiednik czasem sam się narzuca, a czasem jego sformułowanie wymaga pewnej pomysłowości. Poniżej prezentujemy przykłady zadań o przestrzennych klockach, na różne sposoby "spłaszczane".

Rozmaite zagadnienia można wygodnie i ładnie ilustrować geometrycznie. Jeśli wyniki doświadczenia losowego dają się zinterpretować jako punkty pewnego obszaru i każdy wynik jest jednakowo prawdopodobny, to prawdopodobieństwo określonego zdarzenia można wyznaczyć jako stosunek miary (pola, objętości etc.) odpowiadającej mu części obszaru do miary całości.

Dwie nierównoległe płaszczyzny przecinają się wzdłuż prostej. Ta niepozorna obserwacja bywa bardzo przydatna.

Na pierwszym etapie XI Olimpiady Matematycznej Gimnazjalistów pojawiło się pytanie, na które tylko 24% uczestników odpowiedziało poprawnie...

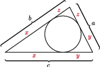
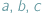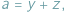
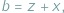
Jeśli w nierówności, którą chcemy uzasadnić, występują długości boków pewnego trójkąta, często przydaje się podstawienie Raviego: 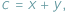gdzie 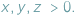Takie liczby 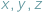zawsze istnieją, są to bowiem długości odcinków stycznych do okręgu wpisanego w trójkąt.

W wielu zadaniach należy uzasadnić, że pewne trzy proste przecinają się w jednym punkcie. Często można wykazać, że wszystkie one są symetralnymi, dwusiecznymi, wysokościami albo środkowymi pewnego trójkąta, co oczywiście kończy dowód.

Skoro dwusieczna to półprosta dzieląca kąt na dwa równe kąty, to dlaczego dwusieczne kątów wewnętrznych każdego trójkąta przecinają się w jednym punkcie? Otóż...

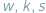Oznaczmy przez liczby odpowiednio wierzchołków, krawędzi i ścian wielościanu. W każdym wierzchołku schodzą się co najmniej trzy końce krawędzi i każda krawędź ma dwa końce, zatem 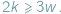Podobnie każda ściana ma co najmniej trzy boki, a każda krawędź należy do dwóch ścian, więc 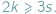Ponadto jeśli wielościan jest wypukły, zachodzi wzór Eulera: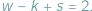

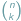Symbol Newtona dla liczb całkowitych 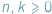oznacza liczbę sposobów wybrania zbioru 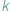elementów spośród 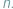W szczególności

Poniższe zadania łączy to, że do rozwiązania każdego z nich można użyć pewnego Bardzo Znanego Twierdzenia, udowodnionego całkiem niedawno. Oczywiście to, że można strzelać z armaty do muchy nie oznacza, że zawsze trzeba...

Tym razem o obrotach na płaszczyźnie...

Izometrią nazywamy przekształcenie, które nie zmienia odległości między punktami. Obrazy trzech niewspółliniowych punktów jednoznacznie ją wyznaczają. Twierdzenie Chaslesa głosi, że każda izometria płaszczyzny jest przesunięciem, obrotem lub symetrią z poślizgiem.

Twierdzenie o stycznej i cięciwie jest niezwykle prostym, a zarazem ogromnie przydatnym faktem z elementarnej geometrii...

Jedną z najsłynniejszych niemożliwych rzeczy w matematyce jest konstrukcja samym cyrklem i linijką kwadratu o polu równym polu danego koła. Problem ten, zwany kwadraturą koła, rozważano już w starożytnej Grecji, ale rozwiązano go, czyli udowodniono niekonstruowalność, dopiero w XIX wieku.

W rozwiązaniach wielu zadań kluczowe jest rozłożenie danej bryły tak, by uzyskać jej siatkę. Jeśli z kolei chcemy zbudować model wielościanu, często rysujemy jego siatkę, wycinamy, składamy... Siatki to przydatne narzędzie, jednakże - jak to z narzędziami bywa - trzeba ostrożnie się nimi posługiwać. Proszę ocenić poprawność poniższych trzech stwierdzeń.

W wielu zadaniach występują różnokolorowe punkty płaszczyzny, a w ich rozwiązaniach przydatne bywają rozmaite rozumowania kombinatoryczne.

W geometrii rzutowej przyjmujemy, że każde dwie proste równoległe przecinają się w pewnym ustalonym punkcie w nieskończoności, odpowiadającym ich kierunkowi, oraz że wszystkie takie punkty w nieskończoności tworzą prostą ("horyzont"). Poniżej przedstawiamy przykłady pojęć i twierdzeń rzutowych oraz ich zastosowań; dopuszczamy w nich takie właśnie punkty przecięcia "na horyzoncie".

Istnieje zaskakujący związek między okręgiem wpisanym w trójkąt i okręgiem na nim opisanym.

Korzystając z tytułowego pomysłu oraz z rysunku lub drobnych jego modyfikacji, można udowodnić szereg twierdzeń z różnych działów matematyki.

Oto dwa zupełnie niepodobne zadania, które można rozwiązać w zaskakująco podobny sposób. W obydwu przypadkach rozwiązanie okazuje się znacznie prostsze, niż można by się w pierwszej chwili spodziewać.

Przekształcenie afiniczne płaszczyzny to takie różnowartościowe przekształcenie płaszczyzny w siebie, przy którym obrazem każdej prostej jest prosta. Wszystkie podobieństwa spełniają te warunki, ale nie tylko one...

Oto kilka krótkich zagadek do szybkiego rozwiązania w wolnym czasie.