Rezultaty
Poniżej przedstawiamy rezultaty niektórych zwycięskich prac.
- Zbigniew Jelonek, Pewna analogia, 1980
Stożek to zbiór prostych mających wspólny punkt (lub kierunek) i przecinających pewną krzywą stopnia 2; stożek dualny to zbiór płaszczyzn mających wspólny punkt (lub kierunek) i stycznych do pewnej krzywej stopnia 2. Współstożkowość oznacza należenie do tego samego stożka. W pracy podane są analityczne warunki na to, by szóstka prostych (płaszczyzn) była współstożkowa. Wynika z tego wiele geometrycznych faktów, np.: elipsoida jest sferą wtedy i tylko wtedy, gdy istnieje 6 płaszczyzn współstożkowych przechodzących przez jej środek i wycinających z niej przekroje o równych polach. - Jarosław Wróblewski, Wokół kongruencji w pierścieniu liczb algebraicznych całkowitych, 1981
Liczby algebraiczne całkowite to pierwiastki wielomianów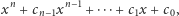
gdzie
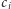 są całkowite; zbiór tych liczb oznaczmy przez
są całkowite; zbiór tych liczb oznaczmy przez 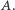 Zbiór liczb postaci
Zbiór liczb postaci 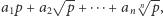 gdzie
gdzie 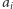 są całkowite, oznaczmy przez
są całkowite, oznaczmy przez 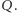 Dla
Dla 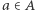 zapiszemy
zapiszemy 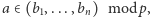 gdy
gdy 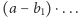
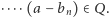 Główny wynik pracy to twierdzenie jeśli
Główny wynik pracy to twierdzenie jeśli 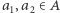 oraz
oraz 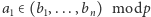 i
i 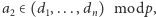 to (1)
to (1) 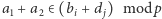 (
( 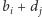 to układ złożony ze wszystkich możliwych sum tej postaci dla
to układ złożony ze wszystkich możliwych sum tej postaci dla 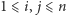 ); (2)
); (2) 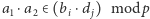 ; co pociąga za sobą (3) dla dowolnego wielomianu
; co pociąga za sobą (3) dla dowolnego wielomianu 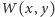 o współczynnikach całkowitych
o współczynnikach całkowitych 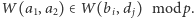 Wynika z tego wiele konsekwencji, w szczególności np. liczba
Wynika z tego wiele konsekwencji, w szczególności np. liczba 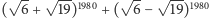 jest liczbą całkowitą, której ostatnią cyfrą jest 2.
jest liczbą całkowitą, której ostatnią cyfrą jest 2. - Mariusz Skałba, O pewnym problemie z elementarnej teorii liczb, 1982
W pracy znajduje się ulepszenie dowodu Andrzeja Schinzla twierdzenia, że 7 jest jedyną liczbą pierwszą spełniającą, przy naturalnych i
i 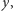 równanie
równanie 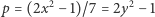
(patrz W. Sierpiński, Teoria liczb cz. II) oraz uogólnienie tego faktu, a mianowicie Dla
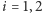 trójmiany kwadratowe
trójmiany kwadratowe 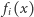 mają współczynniki wymierne;
mają współczynniki wymierne; 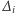 to ich wyróżniki, a
to ich wyróżniki, a 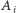 to współczynniki przy
to współczynniki przy 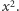 Jeśli
Jeśli 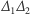 jest kwadratem liczby wymiernej oraz
jest kwadratem liczby wymiernej oraz 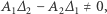 to istnieje co najwyżej skończenie wiele takich liczb pierwszych
to istnieje co najwyżej skończenie wiele takich liczb pierwszych 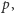 że
że 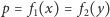 dla pewnych
dla pewnych 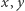 całkowitych.
całkowitych.
Ponadto podany został też algorytm znajdowania wszystkich tych liczb pierwszych. - Michał Wojciechowski, O pewnym rozkładzie figur środkowo symetrycznych, 1984
Praca powstała z okazji zamieszczonego w Wiadomościach Matematycznych t. XXIII.I zadania: Udowodnić, że jeżeli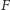 jest płaską figurą ograniczoną, mającą środek symetrii należący do niej, to nie można jej rozłożyć na dwie rozłączne figury przystające.
jest płaską figurą ograniczoną, mającą środek symetrii należący do niej, to nie można jej rozłożyć na dwie rozłączne figury przystające.
Praca zawiera kontrprzykłady, a więc przykłady figur spełniających założenia i dających się rozłożyć na figury przystające, a nawet spełniające dodatkowe warunki, jak spójność czy przeliczalność. W dalszej części pracy jest dowód, że gdy zażądamy, aby części, na które dzielimy, były nie tylko przystające, ale jeszcze środkowo symetryczne, to podział będzie już niemożliwy. - Krzysztof Oleszkiewicz, Skacząc po stożkowych, 1989
Praca poświęcona jest poszukiwaniu punktów kratowych na stożkowych danych równaniami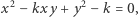
gdzie
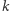 jest ustaloną liczbą całkowitą. Podstawowym spostrzeżeniem jest fakt, że gdy punkt
jest ustaloną liczbą całkowitą. Podstawowym spostrzeżeniem jest fakt, że gdy punkt 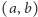 leży na tej stożkowej, to leżą na niej również punkty
leży na tej stożkowej, to leżą na niej również punkty 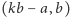 i
i 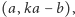 co - gdy jeden z punktów jest kratowy - pozwala znajdować dalsze takie punkty. Wszystkie znalezione przez powtarzanie tego spostrzeżenia punkty to trajektoria punktu
co - gdy jeden z punktów jest kratowy - pozwala znajdować dalsze takie punkty. Wszystkie znalezione przez powtarzanie tego spostrzeżenia punkty to trajektoria punktu 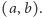 Uzyskany wynik jest następujący:
Uzyskany wynik jest następujący: gdy
gdy 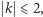 punkty kratowe istnieją tylko dla
punkty kratowe istnieją tylko dla 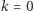 (jeden,
(jeden, 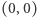 ) i dla
) i dla 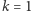 (cztery,
(cztery, 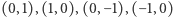 ).
). gdy
gdy 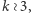 punkty kratowe istnieją tylko dla
punkty kratowe istnieją tylko dla 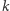 będącego kwadratem liczby naturalnej i wtedy każdy z nich należy do trajektorii pewnego z punktów
będącego kwadratem liczby naturalnej i wtedy każdy z nich należy do trajektorii pewnego z punktów 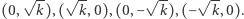
 gdy
gdy 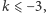 punkty kratowe istnieją tylko dla
punkty kratowe istnieją tylko dla 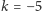 ; są to wówczas punkty z wszystkich trajektorii następujących ośmiu punktów
; są to wówczas punkty z wszystkich trajektorii następujących ośmiu punktów 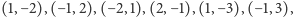
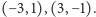
- Marek Pycia, Pewne nierówności funkcyjne, 1992
Nierówność funkcyjna to problem znalezienia wszystkich funkcji, które spełniają dla wszystkich swoich argumentów daną nierówność. W pracy rozważana była nierówność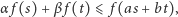
gdzie
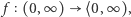 stałe
stałe 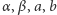 są dodatnie i
są dodatnie i 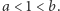 Było to uogólnienie znanego (od niedawna) wyniku dla
Było to uogólnienie znanego (od niedawna) wyniku dla 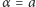 i
i 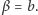 Podstawowy rezultat pracy to stwierdzenie: jeśli ta nierówność ma rozwiązanie niezerowe, to ma rozwiązanie potęgowe. Pozwoliło to na opisanie klas rozwiązań tej, jak też przeciwnej nierówności.
Podstawowy rezultat pracy to stwierdzenie: jeśli ta nierówność ma rozwiązanie niezerowe, to ma rozwiązanie potęgowe. Pozwoliło to na opisanie klas rozwiązań tej, jak też przeciwnej nierówności.