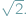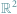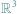Delta mi!

Tak jak problemy praktyczne prowadzą do równań, tak równania prowadzą czasem do nowych rodzajów liczb. Ambitny kmieć z czasów Mieszka I, będący właścicielem trzech krów i marzący o nabyciu (lub zdobyciu) dodatkowych sztuk bydła tak, by stać się szanowanym posiadaczem tuzina krów, musiał niewątpliwie rozwiązywać zadanie matematyczne, które dziś zapisujemy równaniem 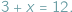Gdy zamienimy występujące tu liczby miejscami, otrzymamy równanie 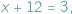które "nie da się rozwiązać": gołym okiem widać, że wśród liczb, za pomocą których zwykliśmy liczyć krowy (czyli liczb naturalnych), nie znajdzie się żadna, która by spełniała to równanie...

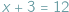Rozwiązywanie równań wymuszało poszerzenie zasobu liczb, jakimi się posługiwano. Równanie można było rozwiązać, posługując się najnaturalniejszymi liczbami, zwanymi zresztą naturalne, ale równanie 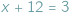wymagało rozszerzenia ich zasobu do liczb całkowitych. Wyjście poza obręb równań pierwszego stopnia pokazało, że do rozwiązania np. równania 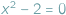nie wystarczą nie tylko liczby całkowite, ale nawet wszystkie liczby wymierne, czyli ułamki 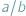zbudowane z liczb całkowitych. Aby uzyskać rozwiązanie, do liczb wymiernych trzeba dołączyć nowe liczby, a wśród nich liczbę niewymierną

Gdy odbywam długie spacery, pewien fakt nieustannie zwraca moją uwagę. O ile zachowuję stałą długość kroku, wciąż zdarza się, że następuję na linie oddzielające kolejne płyty chodnika. Dlaczego tak się dzieje?

Płaszczyznę można wyposażyć w działania dodawania i mnożenia jej punktów. Dlaczego nie można tego zrobić z przestrzenią ?