Piłka w puszce
Piłki tenisowe na ogół pakowane są w rurkę po kilka sztuk. Wyobraźmy sobie piłki tak cenne, że pakowane są każda oddzielnie. Takie opakowanie to z matematycznego punktu widzenia walec...
Piłki tenisowe na ogół pakowane są w rurkę po kilka sztuk. Wyobraźmy sobie piłki tak cenne, że pakowane są każda oddzielnie. Takie opakowanie to z matematycznego punktu widzenia walec...
...jeśli ma się 5 jego punktów. No, może trochę przesadziłem... Okręgu tak dosłownie nakreślić nie można, ale można narysować jego kolejnych kilka punktów, nawet gdy te kilka to np. 100 -- oczywiście, im większa będzie to liczba, tym dłużej będzie to trwało, bo rysować będziemy te punkty kolejno, po jednym.
Przecięcie stożka płaszczyzną
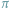 nieprzechodzącą przez wierzchołek to
stożkowa...
nieprzechodzącą przez wierzchołek to
stożkowa...

Okładka Delty 1/1974
Ten numer zamyka czterdzieści lat miesięcznika Delta. Numer próbny został wydrukowany 8 grudnia 1973 roku w nakładzie 50 egzemplarzy, a równo z Nowym Rokiem został wydany w nakładzie 30 tys. identyczny z nim numer 1. Wiąże się z tym anegdotka: nie uwzględniliśmy ingerencji cenzury, bo tak się z niej śmialiśmy, że zapomnieliśmy to zrobić – chodziło o to, by nie ujawniać wielkości obszaru Instytutu Fizyki Jądrowej w Krakowie.
Każdy wie, co to są dwusieczne kątów – tutaj będziemy mówili o trójsiecznych, czyli prostych dzielących kąt (i jego kąt wierzchołkowy) na trzy równe częsci. Zatem trójsieczne są dwie. Mają one dziwną własność zwaną twierdzeniem Morleya.
Zawód matematyka ma wiele zalet...
Symetralna to oś symetrii odcinka, a dwusieczna – kąta. W trójkącie tak symetralne, jak dwusieczne, przecinają się w jednym punkcie.
W -V wieku Parmenides stworzył szkołę filozoficzną, która postawiła sobie za cel zbadanie, jak ma się rozpowszechniona w tamtych czasach opinia, iż matematyka głosi najgłębszą prawdę o świecie, do rzeczywistości. Bez trudu dało się bowiem zauważyć, że pojęcia matematyki – taka, na przykład, prosta, albo – jeszcze bardziej – punkt, nijakich materialnych odpowiedników nie mają. Obiekt materialny można dzielić na mniejsze kawałki, ale przecież w końcu gdzieś będziemy musieli się zatrzymać, choćby z tego powodu, że nie można w skończonym czasie wykonać nieskończenie wielu czynności. Tymczasem matematyka pozwala choćby na odcinanie od odcinka stale połowy tego, co jeszcze zostało do dyspozycji, bez końca, a nawet pozwala stwierdzić, że w końcu z tego odcinka nic nie zostanie, nawet koniec.
Słowa, którymi będziemy się zajmowali, będą napisami złożonymi z liter jednego lub kilku zbiorów (na początek przyjmijmy, że zbiory są dwa – jeden zawiera małe litery łacińskie, a drugi duże) o tej własności, że dwie jednakowe litery umieszczone po kolei będą znikały. Napis, w którym wszystko znikło (czasem i taki jest potrzebny), będzie oznaczany 1.

W Delcie 6/2011 artykuł Marii Donten-Bury o płaszczyźnie rzutowej został poprzedzony przedstawieniem sześciu jej (płaszczyzny, nie Marysi) postaci, pod jakimi daje się nam ona zaobserwować. Wobec tego, że postacie te są bardzo różnorodne, nasunąć się może wątpliwość, czy faktycznie wszystkie są wcieleniami tego samego matematycznego obiektu. Poniżej jest przedstawiony sposób, jak tę wątpliwość można rozstrzygnąć.
Już przed laty, gdy brałem udział w tworzeniu jednej z kolejnych reform nauczania matematyki, miałem poważne wątpliwości, czy umieszczanie w programach nauczania matematyki (podstawach programowych, wykazach efektów nauczania, podręcznikach itp.) działu logika jest zgodne ze zdrowym rozsądkiem.

W wielu miejscach można przeczytać czy usłyszeć, że matematyka, a zwłaszcza geometria jest nauką aksjomatyczną i wszelkie zawarte w niej fakty uzyskuje się właśnie z aksjomatów przez podporządkowane prawom logiki dowody.
Stereometria Stowarzyszenie na rzecz Edukacji Matematycznej
Panuje przekonanie, że w nauczaniu matematyki powinno się eksponować fakt, że ma ona zastosowania. Gdy przyjrzeć się podręcznikom, a zwłaszcza testom kwalifikacyjnym, trudno oprzeć się wrażeniu, że są to rzeczy w stylu mierzenia wysokości piramidy za pomocą długości jej cienia i twierdzenia Talesa, lub też zadań w stylu: jeśli dwóch robotników kopie rów w ciągu 2 godzin, to ilu ich potrzeba, aby ten rów wykopać w 15 sekund? (odpowiedź: 1440).
Historia i filozofia nauk Drobiazgi
Jest taki zdumiewający moment w dziejach świata, gdy my, ludzie, uznaliśmy za
niezbędne udzielenie odpowiedzi na pytanie, co właściwie wyróżnia nas spośród
wszelkich żywych stworzeń. Było to w wieku
 VI. Owa niezbędność
pojawiła się we wszystkich stronach świata, we wszystkich kulturach i – co jeszcze
dziwniejsze, wobec braku możliwości bezpośredniego, a choćby nawet sensownie
szybkiego kontaktu – pojawiła się jednocześnie.
VI. Owa niezbędność
pojawiła się we wszystkich stronach świata, we wszystkich kulturach i – co jeszcze
dziwniejsze, wobec braku możliwości bezpośredniego, a choćby nawet sensownie
szybkiego kontaktu – pojawiła się jednocześnie.
W poprzednim numerze Delty przedstawiłem trzy dowody V postulatu Euklidesa. Dla wszystkich Czytelników było jasne, że zawierają one błędy. Fakt, że mimo to każdy z nich przez pewien czas był uznany za poprawny, wskazuje na ogromny kłopot, jakim dla myślicieli – już niekoniecznie matematyków – było przyjęcie do wiadomości, że mogą istnieć dwie wykluczające się, ale poprawne, a więc w szczególności niesprzeczne teorie opisujące ten sam obiekt, w tym przypadku przestrzeń. A przecież przestrzeń, w której „odbywa się” Wszechświat, jest jedna.
Oczywiście, V postulatu Euklidesa nie da się dowieść na podstawie poprzednich czterech. Niemniej jednak praktycznie każdy znaczący matematyk od V do XIX wieku taki dowód przeprowadził i dopiero jego koledzy wskazywali, w którym miejscu rozumowania użył przesłanki z czterech początkowych postulatów niewynikającej...
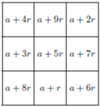
Zamieszczony w poprzednim numerze, jako zapowiedź tego numeru, widoczny obok
kwadrat magiczny jest dla
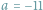 (lub
(lub
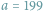 ) i
) i
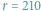 złożony
z samych liczb pierwszych.
złożony
z samych liczb pierwszych.
Gry, zagadki, paradoksy Drobiazgi
W Delcie 3/1979 zamieściliśmy największy znany wówczas kwadrat magiczny złożony z różnych liczb pierwszych – było ich 169. Co więcej, był to kwadrat „cebulkowy”. A dziś – proszę: istnieje już „cebulkowy” kwadrat magiczny aż o trzy większy, złożony zatem z dwustu pięćdziesięciu sześciu liczb pierwszych. I jak tu nie wierzyć w postęp!
Sophie Germain (1776–1831), wbrew ówczesnym obyczajom matematyk, fizyk, metalurg i autorka ciekawych szkiców o kulturze, prawie na każdym kroku musiała udowadniać swą wiedzę i bronić swych dokonań przed rzeszami niedowiarków.
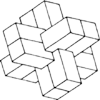
Gry, zagadki, paradoksy Drobiazgi
Wbrew oczywistemu skojarzeniu nie chodzi tu o Konrada Wallenroda, lecz o układankę, jaką przed wiekami wymyślili litewscy drwale...
W Delcie 6/2011 Jerzy Zabczyk przytoczył anegdotę o Feynmanie w związku z pewnym geometrycznym zadaniem efektownie umieszczonym przez Hugona Steinhausa w Kalejdoskopie matematycznym (o czym Feynman nie wiedział) i zaproponował Czytelnikom atrakcyjne zadania.
Girard DESARGUES, matematyk, architekt ogrodów, doradca kardynała Richelieu (a więc rówieśnik Atosa, Portosa i Aramisa) postawił kolegom ogrodnikom pytanie: Jak posadzić 10 drzew w dziesięciu rzędach po 3 drzewa w każdym rzędzie?
Historia i filozofia nauk Drobiazgi
...dwaj najmłodsi uczniowie Galileusza, Bonaventura Cavalieri i Evangelista Torricelli, byli ludźmi do tego stopnia pogodnymi i pełnymi poczucia humoru, że nawet podczas pracy naukowej robili sobie wzajemnie zaawansowane psikusy ku uciesze znajomych.
Biolodzy zapewne mają rozmaite sposoby na umiejscowienie w czasie momentu, gdy nasi przodkowie dosłużyli się miana CZŁOWIEK i pewnie kłócą się o to, które kryteria powinny być uznane za najistotniejsze. Gdy jednak sięgnąć do historii kultury, moment taki jest dość zgodnie nazywany i dyskutować można tylko na temat jego kalendarzowego usytuowania. Tym momentem jest przełom neolityczny.
Gry, zagadki, paradoksy Mała Delta
Oglądając szpargały, jakie w sposób nieunikniony gromadzą się w redakcyjnych szufladach, znalazłem plan lekcji wydany przez Deltę latem 1982 roku – kartonik, format B4.
Jeśli liczba naturalna
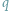 jest największą liczbą pierwszą, to...
jest największą liczbą pierwszą, to...
Zwykłe siodło do konnej jazdy ma dwa łęki i dwie klapy – z przodu i z tyłu jest podniesione do góry, z obu boków opada w dół. Jest przy tym wszędzie krzywe, czyli niepłaskie...
W numerze poświęconym mierze (8/2008) nie sposób pominąć tych pierwszych, czyli zwykłych miar geometrycznych (zważmy, że geometria ma miarę w swojej nazwie).Wydaje się, że wiemy o nich wszystko, bo przecież stykaliśmy się z nimi niemal od zerówki. Okazuje się jednak, że i na ich temat można postawić pytania o nieoczywistych odpowiedziach.
Joseph Louis Lagrange (1736--1813) był ogromnie zniesmaczony ciągle nieudanymi próbami ścisłego zdefiniowania koniecznego dla zastosowań matematyki pojęcia pochodnej funkcji. Rzecz udawała się właściwie tylko dla wielomianów.
Prawie dwieście lat temu Augustin Cauchy udowodnił, że wielościan wypukły, który ma sztywne ściany, jest cały sztywny, choćby jego krawędzie były wyposażone w najlepsze zawiasy. I postawił problem, czy założenie wypukłości jest konieczne.
Każdy wie, jak ułożyć posadzkę, mając do dyspozycji trójkątne kafelki. Jeden ze sposobów jest taki: obok każdego trójkąta kładziemy trójkąt będący jego odbiciem względem środka jego boku. Którego? Każdego. Gdy będziemy tak konsekwentnie postępowali, możemy wyparkietować całą płaszczyznę.
Geometrie nieeuklidesowe Mała Delta
czyli geometryczny odpowiednik szczególnej teorii względności, to dzieło Hermanna Minkowskiego (1864–1909), u którego zresztą Einstein studiował na politechnice w Zurichu. Pierwsza publikacja na ten temat ukazała się w 1909 roku i to tak nieszczęśliwie, że zmarły nagle Minkowski jej nie zobaczył.
Martin Gardner urodził się 21 października 1914 r., a zmarł 22 maja 2010 r. Dwadzieścia pięć lat (1956–81) z jego długiego żywota zajęło redagowanie kącika matematycznego w Scientific American. I można by dopisać tu listę jego książek i artykułów. Ale to byłoby bez sensu. Bo o tym, co człowiek zrobił naprawdę, decyduje jedynie to, co w świecie po jego śmierci jest – dzięki niemu – inne, niż gdy się rodził.
Na ile sposobów można przykryć banknotem prostokąt o tych samych rozmiarach? xxx Każdy od razu zgadnie, że na cztery sposoby: do góry orłem, przy czym orzeł może być do dołu lub do góry nogami, i podobnie na dwa sposoby królem do góry (choć na banknocie nie widać jego nóg).
Gdy do wielomianu
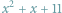 podstawiać będziemy kolejno liczby
podstawiać będziemy kolejno liczby
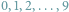 , otrzymamy
, otrzymamy
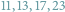 ,
,
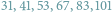 – same
liczby pierwsze. Reguła czy przypadek?
– same
liczby pierwsze. Reguła czy przypadek?