Delta mi!

Jak co miesiąc, trzy ciekawe zadania z matematyki...

Wielomian jaki jest, każdy widzi. I każdy, kto widzi, wie również, że wielomiany miewają pierwiastki rzeczywiste (czyli miejsca zerowe), ale nie zawsze...

Jak co miesiąc, trzy ciekawe zadania z matematyki...

Jak co miesiąc, trzy ciekawe zadania z matematyki...

Jak co miesiąc, trzy ciekawe zadania z matematyki...

Jak co miesiąc, trzy ciekawe zadania z matematyki...

Być może nie wypada zadawać tytułowego pytania w numerze marcowym, gdyż w tym miesiącu obchodzone jest wspaniałe święto tej największej bodaj celebrytki pośród liczb rzeczywistych, jednak Delta nie pozwoli zakneblować sobie ust poprawnością polityczną. Tym bardziej, że w Internecie roi się od plotek i pogłosek na ten temat. Zamieszanie rozpoczęło się od utworzonego w dobrej wierze memu (zamieszczony poniżej), którego autor w poetycki sposób opisywał rzekomą, mistyczną własność 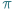- jej rozwinięcie dziesiętne miałoby skrywać wszelkie tajemnice tego świata i odpowiedzi na wszystkie fundamentalne dla ludzkości pytania.

Jak co miesiąc, trzy ciekawe zadania z matematyki...

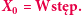W roku 2009 słowem dziesięciolecia stowarzyszenie American Dialect Society ogłosiło czasownik to google, którego polski odpowiednik - guglować/guglać - omawiany jest już na stronach Słownika Języka Polskiego, PWN. Nic dziwnego, wszak korzystanie z wyszukiwarki Google stało się elementem codzienności większości z nas i nie mamy skrupułów przed zadawaniem jej pytań o najbłahsze sprawy. Idąc za myślą przewodnią tego numeru Delty, o nieoczekiwanych związkach teorii z rzeczywistością, pokażemy, co wspólnego ma wszędobylska wyszukiwarka z teorią łańcuchów Markowa, sformułowaną w początkach XX wieku.

W poprzednim odcinku naszej sagi przedstawiliśmy miłosną historię Aldony i Bogumiła. Poniżej prezentujemy jej dość dramatyczną kontynuację, widzianą oczami Aldony...

Człowiek to istota nie tylko myśląca, ale i mierząca - można by rzec górnolotnie, że mierzenie (rozmiarów wrogiej armii, zaopatrzenia spichrzów, stanu skarbca itp.) leży u podstaw naszej cywilizacji. W języku matematyki miara jest definiowana przez następujące, zdroworozsądkowe warunki...

Wyobraźmy sobie następującą wakacyjną historię miłosną, która miała prawo się zdarzyć przed nastaniem ery wszechobecnych mediów społecznościowych...

Jedną z drobnych przyjemności w życiu milionera jest porównywanie swojego bogactwa z bogactwem innych milionerów. Czasem nie jest to trywialne zadanie, gdyż afiszowanie się ze stanem swojego konta (nawet przybliżonym) mogłoby zostać uznane za naruszenie krezusowej etykiety. Istnieje co prawda szeroki wachlarz subtelnych wskaźników, w rodzaju rozmiaru posiadłości czy liczby luksusowych aut, jednak te bywają bardzo mylące. Czy jest możliwa wymiana informacji między dwoma bogaczami w taki sposób, by każdy z nich dowiedział się, który z nich jest bogatszy, i byłaby to jedyna informacja o stanie posiadania rozmówcy?

Ence-pence w której ręce? - za moich dziecięcych lat przedstawiona formułka, której towarzyszyły często dwie wyciągnięte przez wypowiadającą ją osobę ręce, była zwiastunem jakiejś bardzo przyjemnej (najczęściej słodkiej) niespodzianki. Każda wyciągnięta dłoń skrywała bowiem coś dobrego, jednak jako szkrab i tak poświęcałem chwilę zastanowienia nad jej wyborem, będąc świadomym ryzyka, że niewskazana przeze mnie ręka zawiera bardziej atrakcyjny podarek i powędruje on do mojego brata.

Zapewne każdy z czytających te słowa grał kiedyś w marynarza, ale na wypadek gdyby któryś z Czytelników miał smutne dzieciństwo pozbawione tej gry, pokrótce wyjaśnię zasady: na ustalony sygnał każdy z uczestników przedstawia wybraną przez siebie liczbę (najczęściej przy użyciu własnych palców). Następnie rozpoczyna się (cykliczne) wyliczanie uczestników aż do sumy przedstawionych przez nich liczb (oczywiście, należy zawczasu ustalić, od kogo rozpoczyna się wyliczanka). Osoba, na której zakończy się wyliczanie, jest "zwycięzcą" (wziętym w cudzysłów, gdyż "nagrodą" może być, na przykład, zmywanie naczyń)...

Uczciwi złodzieje powinni umieć się dzielić. Oczywiście, dzielić się łupami z innymi uczciwymi złodziejami, którzy pomagali w dokonaniu kradzieży. Można sobie wyobrazić, że taka uczciwość powoduje czasem pewne trudności, gdyż niektóre precjoza mogą być nieskore do podziału. Dla przykładu...

Zacznijmy od następującego zadania: dwunastu Indian (dla ustalenia uwagi i zgrabności tytułu przyjmijmy, że pochodzą oni z plemienia Mohikanów) siedzi dookoła ogniska i pali fajkę pokoju. Procedura rozpoczyna się rzecz jasna od Wodza, który po zapaleniu rzuca zdobytą od bladych twarzy symetryczną monetą i w zależności od wyniku podaje fajkę na lewo albo na prawo. Kolejny Indianin robi to samo - pali faję, rzuca monetą i podaje dalej (fajkę, nie monetę). Nietrudno uwierzyć, że prędzej czy później fajka wpadnie w ręce ostatniego Indianina, który jej wcześniej nie palił (będzie to tytułowy ostatni Mohikanin)...

Rozpoczniemy od żartobliwej, acz pouczającej historyjki: podczas rozmowy dwóch stałych bywalców lokalnego baru jeden z nich mówi do drugiego "Noszenie kaloszy jest bardzo niezdrowe; ilekroć budzę się rano i mam je na nogach, boli mnie głowa"...

Skończyłam! - krzyknęła triumfalnie Agatka do swojego brata, Bartka. Dziewczynka regularnie domaga się od starszego chłopca rozmaitych ciekawostek matematycznych, których ten dowiaduje się w liceum...

Cyberprzestępcy, strzeżcie się! Najmniejszy Wasz ślad nie ukryje się bowiem przed Frankiem Bieżącym, prywatnym detektywem, specjalizującym się w algorytmach wyszukiwania...

Jak można dowiedzieć się z rozlicznych filmów akcji, nieodłączną częścią życia każdego szanującego się tajnego agenta jest wymiana tajnych informacji, najlepiej takich z wielką, czerwoną pieczęcią "Top Secret". Jeśli agent ma taką możliwość, najlepiej przekazać teczkę pełną tajemnic osobiście, jednak jest to luksus, na który może on pozwolić sobie w niewielu sytuacjach, gdyż nierzadko odbiorca tych tajemnic znajduje się na drugim końcu globu. W tej sytuacji konieczne staje się odpowiednie zaszyfrowanie naszych sekretów, aby nawet w przypadku przechwycenia ich przez oślizgłe macki szwarccharakterów, pozostały one sekretami.

Historyjka na marginesie poniżej przedstawia tzw. problem podziału stawki - jedno z zadań, jakimi żywił się raczkujący rachunek prawdopodobieństwa u początków swojego istnienia. W źródłach europejskich pojawia się on po raz pierwszy w podręczniku Summa de Arithmetica, Geometrica, Proportioni, et Proportionalita włoskiego franciszkanina, Luki Paccioliego (1445-1517).

Metoda probabilistyczna gościła już na łamach Delty (np. w numerach 12/2006 i 4/2015), byłoby jednak nieprawdopodobnie głupio pominąć ją w numerze poświęconym dowodom.

Wyobraźmy sobie, że wewnątrz trójkąta 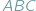umieściliśmy trójkąt 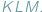Wówczas pole 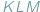nie przekracza, oczywiście, pola 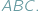Czy możemy stwierdzić to samo o obwodach tych trójkątów? W tym przypadku słowo "oczywiście" również wydaje się uprawnione, Czytelnicy Delty z pewnością wiedzą jednak, jak łatwo o nadużycie tej formułki. Szczęśliwie w tej sytuacji nie pociągałoby to za sobą tragicznych konsekwencji, gdyż istotnie, również obwód trójkąta 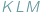nie przekracza obwodu trójkąta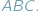

- O żesz krzywa jego źle uwarunkowana macierz! - zakrzyknął generał Estymer, po czym zaklął szpetnie. Na jego biurku leżał stos raportów opisujących kolejny dzień bitwy pomiędzy klanami Częstościowców i Bajesistów. Te dwie frakcje, dzielące między sobą władzę w Statogrodzie, dawno dawno temu pokłóciły się o to, czyje estymatory są dokładniejsze i tak zrodził się konflikt od lat nękający spokojną wcześniej krainę.

Wbrew pozorom tytuł niniejszego tekstu nie jest efektem zestawienia dwóch przypadkowych słów; nawet zupełnie przypadkowe przypadki mogą zdradzać pewne regularności i fakt ten wcale ich przypadkowości nie przeczy. Przypadkiem ich praktycznego zastosowania są średniowieczne tablice do gry w kości; opisane w nich zasady faworyzują jedną ze stron w sposób na tyle delikatny, że oszukiwana strona wcale się taką nie czuje...

Kostką dyskretną wymiaru 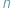nazywamy 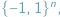czyli zbiór wierzchołków kostki stanowiącej 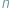-wymiarowy odpowiednik sześcianu...

Zwykła moneta często okazuje się doskonałym narzędziem do rozstrzygania konfliktów. Zapewne każdemu zdarzyło się usłyszeć magiczną formułkę "orzeł to, reszka tamto", z reguły będąc przychylnym dokładnie jednemu ze zdarzeń "to" lub "tamto". Takie rozwiązanie jest jednak mało widowiskowe - o ile wzajemne obrzucanie się inwektywami (w celu wytłumaczenia, w jak wielkim błędzie jest strona przeciwna, prezentując zdanie odmienne od naszego) szybko przyciąga publiczność, tak zakończenie sporu przy użyciu jednego rzutu monetą może pozostawić ją z odczuciem niedosytu.

Wyobraź sobie, Czytelniku, że na skutek wieloletnich ćwiczeń i poznania kilku szulerskich sztuczek udało Ci się zwiększyć swoje szanse na wygraną w grze blackjack do 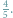Kuszony wizją bajecznego bogactwa w końcu zdecydowałeś się odwiedzić kasyno, by tam spożytkować swoje niesamowite umiejętności. Z miną zawodowego pokerzysty przysiadłeś się do odpowiedniego stolika i zacząłeś grać...

Przeciętny uczeń rozpoczyna podróż po fascynującym świecie geometrycznych konstrukcji uzbrojony w linijkę i kątomierz. Kiedy już nauczyciel uzna swojego podopiecznego za wystarczająco odpowiedzialnego, by nie rysował szkolnych ławek (jakże często zbyt naiwne założenie), uczeń dostaje do ręki kolejne narzędzie walki z czystą kartką papieru, jakim jest cyrkiel...

Zderzenie z asteroidą, wojna nuklearna, globalny potop, przebiegunowanie Ziemi... liczba katastrof oznaczających koniec ziemskiej cywilizacji powinna skłonić nas do traktowania każdego spokojnego poranka, kiedy przewracamy się leniwie z boku na bok zamiast skwierczeć w ogniu Apokalipsy, jako prawdziwego cudu. Mnogość śmiercionośnych zagrożeń sprawia, że ludzkość od zamierzchłych czasów stara się przewidzieć datę (choćby przybliżoną) własnego końca, nie przejmując się zbytnio kolejnymi niepowodzeniami w tej materii. Większość z proponowanych terminów pochodziła od astrologów, numerologów lub przywódców religijnych. Zgodnie z powiedzeniem Hugo Steinhausa "Matematyk zrobi to lepiej" spróbujmy zastanowić się, co ma do powiedzenia w kwestii terminu Końca Świata Królowa Nauk.

Miniony rok przyniósł znaczący wzrost zainteresowania Olimpiadą Matematyczną Gimnazjalistów, a towarzyszył mu szereg inicjatyw Komitetu Głównego mających na celu rzeczone zainteresowanie utrzymać. Jedną z nich było powołanie do życia gazetki Kwadrat, na łamach której znajdują się przeznaczone dla gimnazjalistów artykuły matematyczne oraz wiadomości dotyczące organizacji OMG.