
Oszacujmy pole
Korzystając z tytułowego pomysłu oraz z rysunku lub drobnych jego modyfikacji, można udowodnić szereg twierdzeń z różnych działów matematyki.

Korzystając z tytułowego pomysłu oraz z rysunku lub drobnych jego modyfikacji, można udowodnić szereg twierdzeń z różnych działów matematyki.
Oto dwa zupełnie niepodobne zadania, które można rozwiązać w zaskakująco podobny sposób. W obydwu przypadkach rozwiązanie okazuje się znacznie prostsze, niż można by się w pierwszej chwili spodziewać.
Przekształcenie afiniczne płaszczyzny to takie różnowartościowe przekształcenie płaszczyzny w siebie, przy którym obrazem każdej prostej jest prosta. Wszystkie podobieństwa spełniają te warunki, ale nie tylko one...
Oto kilka krótkich zagadek do szybkiego rozwiązania w wolnym czasie.
Niektóre wielościany są dość dziwne. Intuicja podpowiada, że nie powinny istnieć, a jednak istnieją. Czasem błędne przeczucia wynikają z nazbyt pochopnych uogólnień geometrii płaskiej na przestrzenną, czasem zaś z faktu, że świat wielościanów jest bogatszy, niż się na pierwszy rzut oka wydaje.
Tym razem o twierdzeniu Pascala...
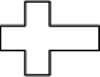
Powierzchnię pewnego wielościanu rozcięto (niekoniecznie wzdłuż krawędzi) i rozłożono, otrzymując płaski wielokąt o kształcie krzyża. Czy wyjściowy wielościan musiał być sześcianem?
Wiele wzorów na sumy kolejnych liczb naturalnych, ich kwadratów, sześcianów itp. można uzasadnić (lub przynajmniej przekonująco zilustrować) na rysunkach. Często rysunki te wymagają niewiele lub nawet zero komentarza – są to tzw. dowody bez słów...
W deltoidzie 7/2013 wykazaliśmy, że odcinek nie jest przeliczalny, posługując się tzw.
metodą przekątniową Cantora. Tym razem udowodnimy ten sam fakt, wykorzystując
pewną dwuosobową grę, której „planszą” jest zbiór
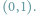
Czasem jeden rysunek pozwala dowieść tak wiele...
Wzór Herona
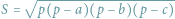 pozwala wyznaczyć pole
trójkąta w zależności od długości jego boków (
pozwala wyznaczyć pole
trójkąta w zależności od długości jego boków (
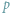 to połowa obwodu).
Czy da się go uogólnić, na przykład dla objętości czworościanu lub pola
czworokąta?
to połowa obwodu).
Czy da się go uogólnić, na przykład dla objętości czworościanu lub pola
czworokąta?
Postawmy czworościan na krawędzi i przez każdą jego krawędź poprowadźmy płaszczyznę równoległą do przeciwległej krawędzi. Takich sześć płaszczyzn wyznacza równoległościan opisany na czworościanie.
Jakie warunki spełniać muszą trzy kąty płaskie, aby można było z nich zbudować wypukły kąt trójścienny, czyli przestrzenne naroże o trzech krawędziach?
W wielu zadaniach geometrycznych należy wykazać, że z pewnych trzech odcinków można zbudować trójkąt. Rozwiązania są zazwyczaj jednego z dwóch rodzajów...
Udowodnimy kilka ewidentnych bzdur, na przykład istnienie okręgu o dwóch środkach
czy równość
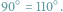 Zachęcam Czytelników do samodzielnego
odszukania błędów w tych dowodach przed lekturą zamieszczonych na końcu
wyjaśnień.
Zachęcam Czytelników do samodzielnego
odszukania błędów w tych dowodach przed lekturą zamieszczonych na końcu
wyjaśnień.
Ile wierzchołków, krawędzi, ścian dwuwymiarowych, trójwymiarowych etc. ma
 -wymiarowy sześcian?
-wymiarowy sześcian?
Czy dwa identyczne rysunki mogą się przydać w jednym zadaniu? Mogą, na przykład gdy drugi jest obrazem pierwszego po pewnej, sprytnie dobranej inwersji...
Czy nieskończoność jest tylko jedna? Nie, istnieją różne, większe i mniejsze!
Tematem poprzedniego deltoidu była inwersja na płaszczyźnie. Analogicznie przekształcenie zdefiniować można w przestrzeni...
Tym razem o inwersji – przekształceniu określanym czasem jako symetria względem okręgu.
Geometria analityczna kojarzona bywa z dużą ilością rachunków, takie rozwiązania często są długie i pracochłonne. Oto kilka przykładów, że nie zawsze jest tak źle.
Rozważmy szachownicę
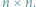 Policzmy dwoma niezależnymi sposobami, ile
jest na niej prostokątów o bokach wzdłuż linii podziału na kratki.
Policzmy dwoma niezależnymi sposobami, ile
jest na niej prostokątów o bokach wzdłuż linii podziału na kratki.
Matematyka Stowarzyszenie na rzecz Edukacji Matematycznej
Jesienna konferencja Stowarzyszenia na rzecz Edukacji Matematycznej chyba już na stałe wpisała się w kalendarz spotkań dotyczących popularyzacji matematyki i pracy z uczniami uzdolnionymi matematycznie. W dniach 26-28 października do Ameliówki koło Kielc przyjechało około 150 nauczycieli matematyki oraz pracowników wyższych uczelni.
Gdzie na płaszczyźnie znajdują się punkty, których stosunek odległości do dwóch
ustalonych punktów
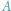 i
i
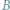 równy jest danej dodatniej stałej
równy jest danej dodatniej stałej
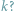

Nazwy miesięcy napisane są na podłużnych ścianach trzech szarych prostopadłościanów na dole, a dni tygodnia na prostopadłościanach na górze.
Gry, zagadki, paradoksy Deltoid
Pewnego grudniowego wieczoru Genowefa zaproponowała swojej siostrze Zenobii...
Matematyka Stowarzyszenie na rzecz Edukacji Matematycznej
W roku szkolnym 2011/2012 zmieniona została formuła Olimpiady Matematycznej Gimnazjalistów. Zmiana ta zaowocowała znacznym wzrostem zainteresowania Olimpiadą. W związku z tym Komitet Główny Olimpiady Matematycznej Gimnazjalistów oraz Stowarzyszenie na rzecz Edukacji Matematycznej zorganizowały w całej Polsce cykl seminariów Poznajemy Olimpiadę Matematyczną Gimnazjalistów.
W wielu problemach matematycznych warto rozważać elementy ekstremalne – największe, najkrótsze, najbliższe... Metoda ta bywa często przydatna w zadaniach dotyczących punktów płaszczyzny lub grafów, czyli punktów łączonych liniami.
Którędy przebiega najkrótsza droga lotnicza z Warszawy do Vancouveru? Wbrew pozorom – mimo podobnej szerokości geograficznej – wcale nie wzdłuż równoleżnika, a nad Grenlandią, o czym łatwo się przekonać, naciągając nitkę na globusie.
Ortocentrum trójkąta to punkt przecięcia jego wysokości. Przyjmijmy oznaczenia jak
na rysunkach 1 i 2 oraz założenie, że trójkąt
 jest ostrokątny.
jest ostrokątny.
Gry, zagadki, paradoksy Deltoid
Strategia wygrywająca w grze to taki „przepis” na nią, który pozwala zawsze wygrać, niezależnie od ruchów przeciwnika. Wiadomo, że w wielu grach któryś z graczy (rozpoczynający lub drugi) ma taką strategię, często nawet można ją konkretnie wskazać. W niektórych przypadkach jest ona właściwie w zasięgu ręki, trzeba tylko ją dostrzec, co nie zawsze jest łatwe.
Gry, zagadki, paradoksy Deltoid
Niektóre gry mogą wydawać się trudne, dopóki gracz się nie dowie, o co tak naprawdę w nich chodzi – wtedy nagle te same gry okazują się łatwe, czasem wręcz oczywiste...

Zastosowania matematyki Deltoid
Kryptografia wizualna to metoda komputerowego szyfrowania obrazów, w której do rozszyfrowania wystarczy... popatrzeć. Konkretniej, z obrazu, który chcemy zaszyfrować („obrazem” może być też napisany na kartce tekst), tworzymy dwa „pstrokate” obrazy, z których nic nie można odczytać.
Poprzedni deltoid poświęcony był osiom potęgowym, między innymi twierdzeniu, które w skrócie brzmi tak: osie potęgowe trzech okręgów przecinają się w jednym punkcie. Ciekawym jego zastosowaniem jest dowód twierdzenia Brianchona.
Nieco więcej o potędze punktu względem okręgu.
Niektóre nierówności, pozornie niezwiązane z geometrią, można zaskakująco łatwo udowodnić, wykorzystując twierdzenie Pitagorasa i prosty geometryczny fakt, że najkrótszą łamaną pomiędzy dwoma punktami jest łączący je odcinek.
Tematem poprzedniego deltoidu był środek ciężkości i związane z nim zadania. W tym numerze pora na zastosowania środka ciężkości w problemach pozornie z nim niezwiązanych. Na marginesie przypominamy podstawowe fakty.
Środek ciężkości to – intuicyjnie – taki punkt, w którym trzeba coś podeprzeć, by owo coś utrzymało się w równowadze. Można go własnoręcznie poszukać na przykład dla długopisu, balansując nim poziomo na palcu.
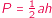
Najpopularniejszy wzór na pole trójkąta to jedna druga podstawa razy wysokość. Proste wnioski z tego wzoru pozwalają rozwiązać niełatwe czasem zadania.
W poprzednim deltoidzie zaprezentowano kilka zadań z geometrii płaskiej, rozwiązanych poprzez „wyjście w przestrzeń”. Oto garść kolejnych przykładów na to, że warto płaskie rysunki postrzegać jako ilustracje sytuacji trójwymiarowych.
Niektóre zadania z geometrii płaskiej łatwiej najpierw rozwiązać w przestrzeni, a później dopiero z powrotem je „spłaszczyć”. Liczne przykłady pojawiły się w deltoidach 17 i 18. Oto jeszcze dwa tego rodzaju problemy.

Niektóre sumy nieskończone można zilustrować, tworząc nieskończony rysunek, którego pewna część jest podobna do całości. Na przykład na rysunku taką częścią jest jego prawa górna ćwiartka, a także prawa górna ćwiartka tej ćwiartki itd.
Gry, zagadki, paradoksy Mała Delta
W pewnym kraju żyło bardzo wielu mędrców. Któregoś dnia groźny król postanowił przekonać się, czy rzeczywiście zasługują oni na to zaszczytne miano i zapowiedział, że czeka ich trudna próba. Zebrał mędrców w swej komnacie i przedstawił im poniższe zasady.
W niektórych zadaniach geometrycznych (i nie tylko) warto dobrze coś ustawić, aby łatwiej rozwiązać problem. Poniżej podaję szereg tego rodzaju przykładów.