Teoria liczb Kącik początkującego olimpijczyka
Lemat o zwiększaniu wykładnika p-adycznego
O zależnościach między 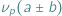 i
i 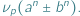
Teoria liczb Kącik początkującego olimpijczyka
O zależnościach między 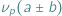 i
i 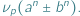
Teoria liczb Kącik początkującego olimpijczyka
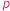 -adyczne
-adyczneO wygodnym narzędziu, przydatnym wszędzie tam, gdzie spotykamy rozkład na czynniki pierwsze
Planimetria Kącik początkującego olimpijczyka
O prostej Eulera i okręgu dziewięciu punktów.
Planimetria Kącik początkującego olimpijczyka
Najbardziej królewskie części trójkąta i ich własności.
Matematyka Kącik początkującego olimpijczyka
O półniezmiennikach, dzięki którym wykazujemy, że pewne przekształcenia można wykonać tylko skończenie wiele razy.
Algebra Kącik początkującego olimpijczyka
Standardowym postępowaniem jest ujednorodnianie dowodzonych nierówności za pomocą danego w zadaniu warunku. Ciekawiej jest na odwrót - gdy mamy udowodnić jednorodną nierówność, możemy często założyć coś dodatkowo o występującej w niej zmiennych. Naprawdę!
Planimetria Kącik początkującego olimpijczyka
O znajdowaniu i dorysowywaniu równoległoboków oraz stosowaniu ich własności.
Gry, zagadki, paradoksy Kącik początkującego olimpijczyka
Rozważamy tutaj gry z udziałem dwóch graczy, którzy podczas rozgrywki mają pełną informację na temat tego, co dzieje się na planszy. Każda gra ma ściśle określone reguły, w tym cel. Gracz, który jako pierwszy go osiągnie, wygrywa, a jego przeciwnik przegrywa, przy czym nie musi być to ten sam cel dla obu graczy.
Teoria liczb Kącik początkującego olimpijczyka
O pożytkach płynących z posługiwania się dziesiętnym systemem pozycyjnym.
Matematyka Kącik początkującego olimpijczyka
Według legendy pod koniec XVIII wieku działa się następująca rzecz. Pewien nauczyciel kazał swoim uczniom dodać wszystkie liczby od 1 do 40, aby mieć przez dłuższą chwilę spokój. Wszyscy, z wyjątkiem jednego, wykonywali pracowicie kolejne dodawania i zazwyczaj popełniali błędy...
Geometria Kącik początkującego olimpijczyka
O stosowaniu trygonometrii w zadaniach olimpijskich.
Algebra Kącik początkującego olimpijczyka
Tożsamości algebraiczne, w których pojawia się suma sześcianów trzech liczb.
Algebra Kącik początkującego olimpijczyka
O licznych zastosowaniach faktu, że dla każdego wielomianu 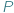 w sumie algebraicznej
w sumie algebraicznej 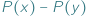 można wyłączyć przed nawias wyrażenie
można wyłączyć przed nawias wyrażenie 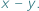
Planimetria Kącik początkującego olimpijczyka
Przedstawiamy wygodne narzędzie geometryczne o wielu zastosowaniach, wśród których znajduje się dowodzenie współliniowości punktów.
Algebra Kącik początkującego olimpijczyka
O stosowaniu podstawowej wiedzy szkolnej na temat funkcji kwadratowej do rozwiązywania zadań olimpijskich.
Planimetria Kącik początkującego olimpijczyka
Gdy w zadaniu występuje kąt o mierze będącej wielokrotnością 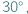 to jest spora szansa na to, że gdzieś tam jest ukryty trójkąt równoboczny.
to jest spora szansa na to, że gdzieś tam jest ukryty trójkąt równoboczny.
Matematyka Kącik początkującego olimpijczyka
O pożytkach płynących z faktu, że niektóre własności obiektów zostają zachowane po poddaniu ich wybranym przekształceniom.
Matematyka Kącik początkującego olimpijczyka
Zadania z wykorzystaniem indukcji prostej, głębokiej i silnej.
Stereometria Kącik początkującego olimpijczyka
Rozpatrując siatkę, odpowiedni przekrój lub rzut, możemy niekiedy sprowadzić zadanie z geometrii przestrzennej do zadania z planimetrii.
Analiza Kącik początkującego olimpijczyka
Kwadrat liczby rzeczywistej jest nieujemny (fanfary!).
Matematyka Kącik początkującego olimpijczyka
O paru zasadach pozwalających stwierdzić, który z dwóch zbiorów ma więcej elementów, ale bez liczenia elementów tych zbiorów.
Planimetria Kącik początkującego olimpijczyka
Związek okręgu opisanego na trójkącie ze środkami okręgu wpisanego i okręgów dopisanych.
Algebra Kącik początkującego olimpijczyka
O wyrażeniach symetrycznych oraz uproszczeniach, które można stosować w rozwiązywaniu zadań z takimi wyrażeniami.
Teoria liczb Kącik początkującego olimpijczyka
Nieoczywiste zastosowania oczywistego stwierdzenia: pomiędzy dwiema kolejnymi liczbami całkowitymi nie ma żadnej liczby całkowitej.