Wszystko to brzmi nieprawdopodobnie - powiecie po przeczytaniu dwóch poprzednich artykułów o mechanice kwantowej. Jak to, najbardziej fundamentalna teoria mikroświata pozwalająca przewidzieć wyniki doświadczeń z fantastyczną dokładnością nie może sobie poradzić z opisaniem losów zwykłego, swobodnego elektronu?!

Niewątpliwie tą teorią fizyczną, która najbardziej współdecyduje o obliczu fizyki współczesnej, jest mechanika kwantowa. Szereg jej twierdzeń i postulatów trudno zrozumieć w świetle naszego doświadczenia codziennego. Toteż właściwie od momentu jej powstania - a upływa właśnie pięćdziesiąt lat, odkąd przyjęła postać niemal definitywną - budziła ona wiele wątpliwości i prowokowała do sprzeciwu. Do dziś szereg kwestii interpretacyjnych nie znalazło jeszcze ostatecznego wyjaśnienia i nie brak fizyków, którzy się spodziewają, że stanie się to w końcu powodem do sformułowania nowej, lepszej teorii...

Za początek nowej, kwantowej ery w fizyce przyjmuje się zazwyczaj rok 1900. Wtedy to właśnie fizyk niemiecki Max Planck odkrył tak zwany kwant działania, którego wielkość, równa

jest uniwersalną stałą fizyczną charakteryzującą procesy zachodzące w świecie obiektów mikroskopowych...

Mechanika kwantowa wprawiała i ciągle jeszcze wprawia matematyków w zakłopotanie, dostarczając tym samym wielu interesujących problemów. Zaczęło się od Diraca, który różniczkował funkcje nieróżniczkowalne i otrzymywał sensowne wyniki. Potrzeba było lat, by rzecz uporządkować: stworzono (zob. Delta 10/1975) teorię dystrybucji, na gruncie której poczynania Diraca nabrały głębokiego matematycznego sensu.

Dzisiejsze nasze eksperymenty będą niestety dostępne tylko dla stosunkowo niewielkiej części zbioru Czytelników "Delty": będzie to przekrój zbioru osób, które zdecydują się na wydatek ponad 80 zł i zbioru (znacznie, jak przypuszczam, mniej licznego) szczęśliwców, którzy natrafią na fotodiodę w sprzedaży. Produkowane w Polsce fotodiody germanowe FG-2, podobnie jak i dowolne inne (także fototranzystory) świetnie nadają się do naszych doświadczeń, cała sztuka w tym, żeby je kupić.

Gdzie te dawne dobre czasy, kiedy zmęczeni i przemarznięci myśliwi wracali z ubitym niedźwiedziem z polowania i grzali się przed ogniskiem, wielbiąc boską, życiodajną moc ognia? Co z tego zostało w Waszych miejskich mieszkaniach? Grzeją Was głupie żelazne rury - kaloryfery, świecą Wam nudne żarówki...

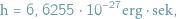
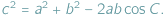Jednym z podstawowych wzorów trygonometrycznych jest twierdzenie kosinusów podające zależność między bokami trójkąta a jednym z jego kątów: Na formułę tę można patrzeć jako na uogólnienie twierdzenia Pitagorasa (do którego sprowadza się, gdy kąt 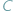jest prosty, czyli

Chociaż są to pojęcia abstrakcyjne (bo przecież nikt nie widział ani punktu, ani odcinka), przemawiają dobrze do wyobraźni i zgadzają się ze zdrowym rozsądkiem. I aż dziw bierze, jak wiele wokół nas zjawisk, które zdają się ostrzegać: uwaga to co wydaje się takie oczywiste, wcale nie musi być prawdziwe.