Może wydawać się dziwne, że tak długo fizycy nie mogli poradzić sobie z wyjaśnieniem przyczyn ruchów Browna, pomimo że stosunkowo wcześnie wysunięto hipotezę, iż ruchy te spowodowane są przez zderzenia atomów ośrodka z cząstką zawiesiny. Przyczyna tkwiła w "zdroworozsądkowym" mniemaniu, że im więcej elementów, większa populacja itp., tym układ jest bardziej jednorodny, tym trudniej zaobserwować odchylenia od wartości średnich. W przypadku ruchów Browna zostało to explicite sformułowane przez botanika Karla Naegeliego w 1879 roku. Korzystając z danych o rozmiarach atomów wyliczył on przeciętną prędkość, jaką może uzyskać ziarenko zawiesiny na skutek zderzenia z jedną molekułą cieczy. Wyszła mu bardzo mała liczba, rzędu jednej tysięcznej 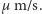Takiego efektu nie da się w żaden sposób zaobserwować pod mikroskopem. I jest to prawda. Ale Naegeli idzie dalej i stwierdza, że ziarenko bombardowane jest przez molekuły cieczy ze wszystkich stron z ogromną częstotliwością (średnio 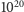razy na sekundę). Jeżeli nawet zostało poruszone w jedną stronę, to natychmiast zostanie zatrzymane na skutek uderzenia z drugiej strony. Smoluchowski pierwszy zrozumiał niesłuszność tego typu rozumowania. Oto fragment z pracy z 1906 roku odnoszący się do argumentu Naegeliego.

Jest to taki sam błąd rozumowania, jak gdyby człowiek uprawiający hazardową grę (np. rzucanie kostki) sądził, że nigdy większej straty ani też większego zysku mieć nie będzie, niż wynosi stawka na jeden rzut. Wiemy dobrze, że szczęście i nieszczęście zwykle niezupełnie się równoważą; że im dłużej gra trwa, tym większa jest przeciętna suma albo wygrana, albo stracona. Pouczające jest obliczenie tego przykładu, w założeniu równego prawdopodobieństwa korzystnych i niekorzystnych rzutów. Rozważając wszystkie możliwe kombinacje, łatwo sprawdzić, że prawdopodobieństwo otrzymania 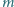korzystnych, 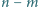niekorzystnych, to znaczy otrzymania ostatecznej nadwyżki 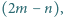wynosi:

Stąd znajdujemy wartość przeciętnego zboczenia w jedną lub drugą stronę:

jeżeli dla uproszczenia liczbę 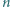przyjmiemy za parzystą. Wyrażenie to można przekształcić przez zastosowanie twierdzenia dwumianowego w formę dogodniejszą:

która dla dużych liczb przechodzi w

Smoluchowski wyciąga na podstawie tego wyniku wniosek, że dla ziarenka pozostanie zatem dodatni lub ujemny nadmiar blisko 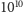uderzeń na sekundę. Ziarenko jednak się poruszy!